中缀表达式转后缀表达式（逆波兰表达式） java详细讲解

为什么需要转换

大家看到，后缀表达式适合计算式进行运算，但是人却不太容易写出来，尤其是表达式很长的情况下，因此在开发中，我们需要将 中缀表达式转成后缀表达式。

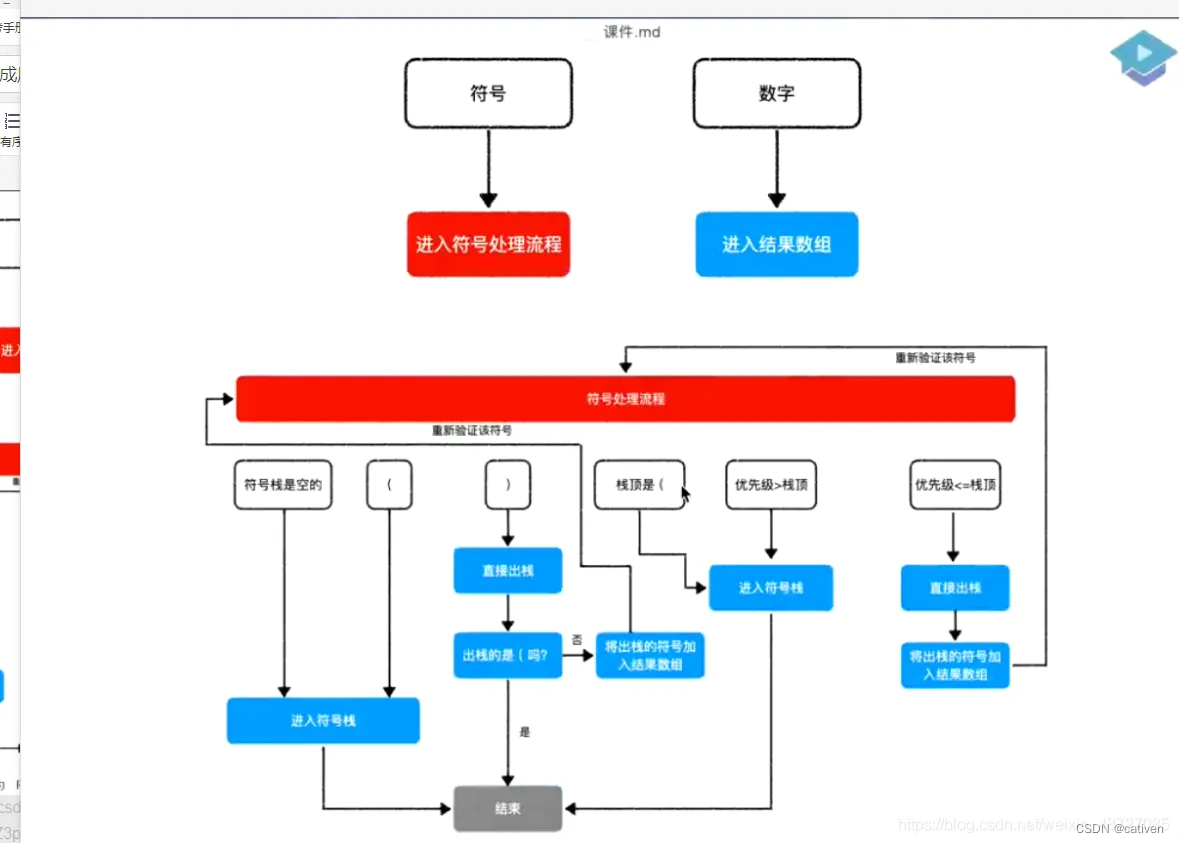
具体的步骤

1. 初始化两个栈：运算符栈s1和储存中间结果的栈s2；
2. 从左至右扫描中缀表达式；
3. 遇到操作数时，将其压s2；
4. 遇到运算符时，比较其与s1栈顶运算符的优先级：
   1.如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
   2.否则，若优先级比栈顶运算符的高，也将运算符压入s1；
   3.否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4.1)与s1中新的栈顶运算符相比较；
5. 遇到括号时：
   (1) 如果是左括号“(”，则直接压入s1
   (2) 如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
6. 重复步骤2至5，直到表达式的最右边
7. 将s1中剩余的运算符依次弹出并压入s2
8. 依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

举例说明

将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程如下，因此结果为 “1 2 3 + 4 × + 5 –”

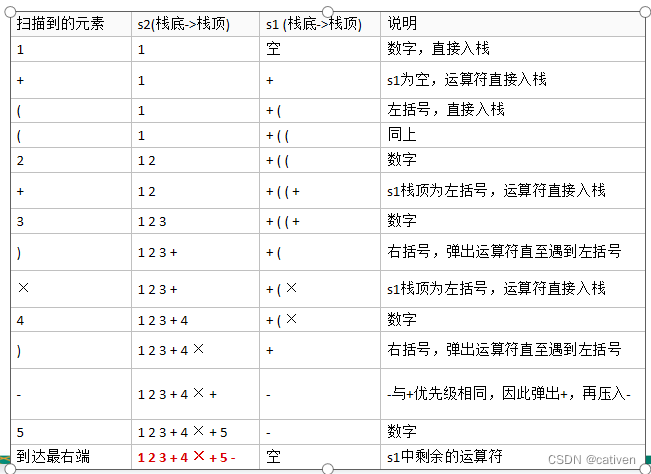
解题思路

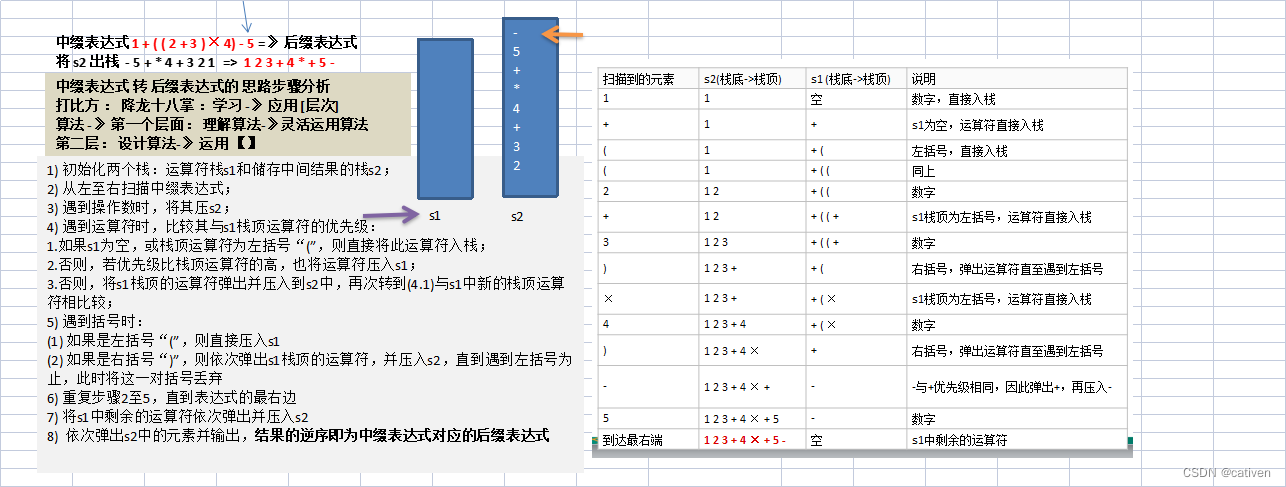
代码实现

package com.qf.stack;import java.util.ArrayList;import java.util.List;import java.util.Stack;public class PolandNation {    public static void main(String[] args) { //(55+6)*2+33-12 String expression="(55+6)*2+33-12"; List<String> splitList = getSplitList(expression); List<String> sufferList = getSufferList(splitList); int cal = cal(sufferList); System.out.println("计算得到的结果："+cal);    }    public static List<String> getStringList(String express){ String[] split = express.split(" "); List<String> list=new ArrayList<>(); for (String s : split) {     list.add(s); } return list;    }    /*从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，    用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；    重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果     */    public static int cal(List<String> list){ Stack<String> stack=new Stack<>(); for (String item : list) {     if (item.matches("\\d+")){  stack.push(item);     }else{  int num1 = Integer.parseInt(stack.pop());  int num2 = Integer.parseInt(stack.pop());  int res=0;  switch (item){      case "+":   res=num1+num2;   break;      case "-":   res=num2-num1;   break;      case "*":   res=num1*num2;   break;      case "/":   res=num2/num1;   break;      default:   break;  }  stack.push(""+res);     } } int res=Integer.parseInt(stack.pop()); return res;    }    //获取中缀表达式的拆分    public static List<String> getSplitList(String express){ List<String> list=new ArrayList<>(); int i=0; String str; do {     if (express.charAt(i)>57||express.charAt(i)<48){  list.add(String.valueOf(express.charAt(i)));  i++;     }else{  str="";  while (i<express.length()&&express.charAt(i)<=57&&express.charAt(i)>=48){      str=str+express.charAt(i);      i++;  }  list.add(str);     } }while (i<express.length()); return list;    }    //1 + ( ( 2 + 3 )× 4) - 5    //把中缀表达式转换为后缀表达式   /* 1) 初始化两个栈：运算符栈s1和储存中间结果的栈s2；     2) 从左至右扫描中缀表达式；     3) 遇到操作数时，将其压s2；     4) 遇到运算符时，比较其与s1栈顶运算符的优先级：     1.如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；     2.否则，若优先级比栈顶运算符的高，也将运算符压入s1；     3.否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4.1)与s1中新的栈顶运算符相比较；     5) 遇到括号时：     (1) 如果是左括号“(”，则直接压入s1     (2) 如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃     6) 重复步骤2至5，直到表达式的最右边     7) 将s1中剩余的运算符依次弹出并压入s2     8)  依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式*/    public static List<String> getSufferList(List<String> list){ //运算符栈s1 Stack<String> operateStack=new Stack<>(); //中间结果 使用ArrayList的原因是因为可以减少后缀表达式的逆序 List<String> tempList=new ArrayList<>(); for (String item : list) {     if (item.matches("\\d+")){  tempList.add(item);     } else if (item.equals("(")){  operateStack.push(item);     }else if (item.equals(")")){  while(!operateStack.peek().equals("(")){      tempList.add(operateStack.pop());  }  operateStack.pop();     }else{  while(operateStack.size()!=0&&Operation.getPrior(item)<=Operation.getPrior(operateStack.peek())){      tempList.add(operateStack.pop());  }  operateStack.push(item);     } } while (operateStack.size()!=0){     tempList.add(operateStack.pop()); } return tempList;    }}class Operation{    public static final int DEV=2;    public static final int MUL=2;    public static final int DEC=1;    public static final int ADD=1;    public static int getPrior(String rex){ int res=0; switch (rex){     case "+":  res=ADD;  break;     case "-":  res=DEC;  break;     case "*":  res=MUL;  break;     case "/":  res=DEV;  break;     default:  System.out.println("未匹配字符");  break; } return res;    }}