❤写在前面：学完了贪心法，咱学学分治法
❤博客主页：努力的小鳴人
❤系列专栏：算法
❤欢迎小伙伴们，点赞👍关注🔎收藏🍔
❤若有误，请小伙伴们指正！🌹

目录

• 🚩分治法(Divide and Conquer)
• 一、分治法概述
• • 🔥实际意义
  • 🔥基本思想
  • 🔥解题步骤
• 二、二分查找
• • 🔥问题描述
  • 🔥算法思想
  • 🔥算法设计
  • 🔥构造实例
  • 🔥算法描述
  • • 👌非递归形式
    • 👌递归形式
  • 🔥算法分析
• 三、循环赛日程表
• • 🔥问题描述
  • 🔥算法思路
  • 🔥构造实例
  • 🔥代码实现

🚩分治法(Divide and Conquer)

一、分治法概述

分治法可以通俗的解释为:把一片领土分解，分解为若干块小部分，然后一块块地占领征服，被分解的可以是不同的政治派别或是其他什么，然后让他们彼此异化

🔥实际意义

任何一个可以用计算机求解的问题所需的计算时间都与其规模有关：问题的规模越小，越容易直接求解

在计算机科学中，分治法是一种很重要的算法。它采取各个击破的技巧来解决一个规模较大的问题，该技巧是很多高效算法的基础，如排序算法(🔎快速排序，归并排序)，傅立叶变换(快速傅立叶变换)等

🔥基本思想

将一个难以直接解决的大问题，分解成一些规模较小的相同问题，以便各个击破，分而治之

🔎补充
分治法的精髓：
分–将问题分解为规模更小的子问题；
治–将这些规模更小的子问题逐个击破；
合–将已解决的子问题合并，最终得出“母”问题的解；

🔥解题步骤

1. 步骤1：分解——即将问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题；
2. 步骤2：治理
     步骤2-1：求解各个子问题
     步骤2-2：合并

🔎补充：
分治法所能解决的问题一般具有以下几个特征：

1. 该问题的规模缩小到一定的程度就可以容易地解决
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
3. 利用该问题分解出的子问题的解可以合并为该问题的解；
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

二、二分查找

🔥问题描述

二分查找又称为折半查找，它要求待查找的数据元素必须是按关键字大小有序排列的

问题描述：给定已排好序的n个元素s1,…,sn，现要在这n个元素中找出一特定元素x

首先较容易想到使用顺序查找方法，逐个比较s1,…,sn，直至找出元素x或搜索遍整个序列后确定x不在其中。显然，该方法没有很好地利用n个元素已排好序这个条件。因此，在最坏情况下，顺序查找方法需要O(n)次比较

🔥算法思想

假定元素序列已经由小到大排好序，将有序序列分成规模大致相等的两部分，然后取中间元素与特定查找元素x进行比较，如果x等于中间元素，则算法终止；如果x小于中间元素，则在序列的左半部继续查找，即在序列的左半部重复分解和治理操作；否则，在序列的右半部继续查找，即在序列的右半部重复分解和治理操作。可见，二分查找算法重复利用了元素间的次序关系

🔥算法设计

1. 步骤1：确定合适的数据结构。设置数组s[n]来存放n个已排好序的元素；变量low和high表示查找范围在数组中的下界和上界；middle表示查找范围的中间位置；x为特定元素
2. 步骤2：初始化：令low=0；high=n-1
3. 步骤3：middle=(low+high)/2，即指示中间元素
4. 步骤4：判定low小于等于high是否成立，如果成立，转步骤5；否则，算法结束
5. 步骤5：判断x与s[middle]的关系：如果x==s[middle]，算法结束；如果x>s[middle]，则令
6. low=middle+1；否则令high=middle-1，转步骤3

🔥构造实例

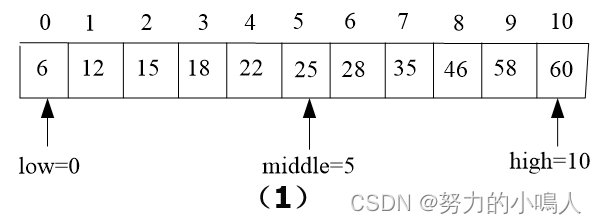
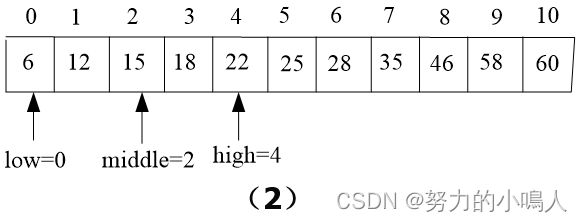
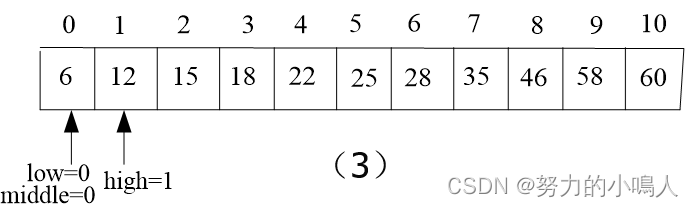
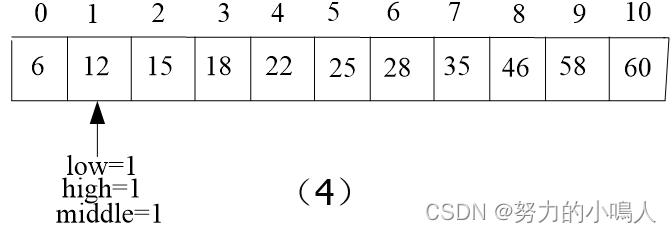
🔥算法描述

有两种形式：非递归形式与递归形式

👌非递归形式

int NBinarySearch(int n,int s[n],int x){int low=0,high=n-1; while(low<=high){int middle=(low+high)/2; if(x==s[middle])  return middle; else if(x>s[middle]) low=middle+1;else high=middle-1; }    return -1;}

👌递归形式

int BinarySearch(int s[n],int x,int low,int high){   if (low>high) return -1;   int middle=(low+high)/2;   if(x==s[middle])  return middle;  else if(x>s[middle]) return BinarySearch (s, x, middle+1, high);else  return BinarySearch (s, x, low, middle-1);}  

🔥算法分析

设定的有序序列中具有n个元素

显然，当n=1时，查找一个元素需要常量时间，因而T(n)=O(1)
当n>1时，计算序列的中间位置及进行元素的比较，需要常量时间O(1)。递归地求解规模为n/2的子问题，所需时间为T(n/2)。
因此，二分查找算法所需的运行时间T(n)的递归形式为：
当n>1时，T(n)=T(n/2)+O(1)
=……
=T(n/2x)+xO(1)
简单起见，令n=2x，则x=logn。
由此T(n)=T(1)+logn=O(1)+O(logn)因此，二分查找算法的时间复杂性为O(logn)

三、循环赛日程表

觉得这个问题很有代表性

🔥问题描述

设有n=2k个运动员要进行羽毛球循环赛，现要设计一个满足以下要求的比赛日程表：
（1）每个选手必须与其它n-1个选手各赛一次；
（2）每个选手一天只能比赛一次；
（3）循环赛一共需要进行n-1天。
由于n=2k，显然n为偶数

🔥算法思路

（1）如何分，即如何合理地进行问题的分解？
             一分为二
（2）如何治，即如何进行问题的求解？
             进行合并
（3）问题的关键——发现循环赛日程表制定过程中存在的规律性

🔥构造实例

n=2¹个选手的比赛日程表的制定

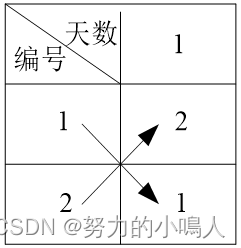
n=2²个选手的比赛日程表的制定


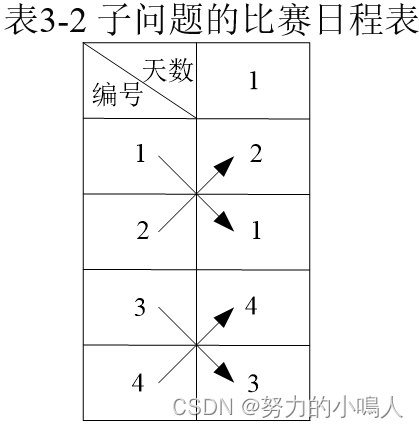
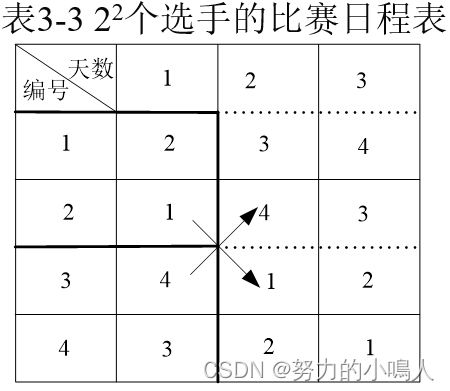
n=2³个选手的比赛日程表的制定

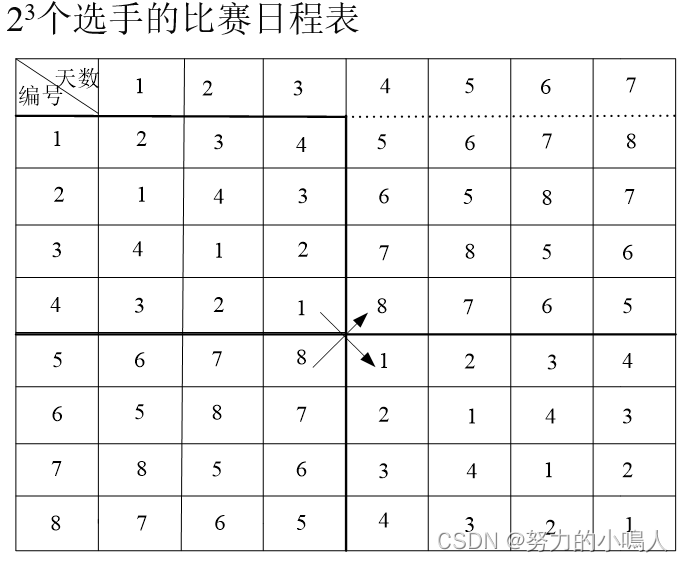
🔥代码实现

#include#include#include#define MAXLENGTH 20//嵌入式内联函数用于计算程序运行所消耗的时间，单位为纳秒inline unsigned GetCyCount(){__asm _emit 0x0f __asm _emit 0x31}int a[MAXLENGTH][MAXLENGTH];//非递归方法void GameTable(int k){int n = 2;int t,temp,i,j;//先定义初始几个元素a[1][1] = 1;a[1][2] = 2;a[2][1] = 2;a[2][2] = 1;for (t = 1; t < k; t++){//代表每一单位的边长temp = n;//代表每一行的最大长度n = n * 2;//填左下角for(i = temp + 1; i <= n; i++)for (j = 1; j <= temp; j++)a[i][j] = a[i - temp][j] + temp;//填右上角for (i = 1; i <= temp; i++)for (j = temp + 1; j <= n; j++)a[i][j] = a[i + temp][j - temp];//填右下角for (i = temp + 1; i <= n; i++)for (j = temp + 1; j <= n; j++)a[i][j] = a[i - temp][j - temp];}}//递归算法void GameTable2(int k,int m){int i, j;if (m==2){a[k][1] = k;a[k+1][1] = k + 1;}else{GameTable2(k, m / 2);GameTable2(k + m / 2, m / 2);}for (i = k; i < k + m / 2; i++){for (j = m / 2 + 1; j <= m; j++){a[i][j] = a[i + m / 2][j - m / 2];}}for (i = k+m / 2; i < k + m; i++){for (j = m / 2 + 1; j <= m; j++){a[i][j] = a[i - m / 2][j - m / 2];}}}void main(){int k,i,j;unsigned long start, finish;printf("请输入K的数值:");scanf("%d", &k);printf("这是非递归算法:\n");start = (unsigned long)GetCyCount();GameTable(k);finish = (unsigned long)GetCyCount();for (int i = 1; i <= pow(2.0, k); i++){printf("第");printf("%d", i);printf("天");}printf("\n");for (i = 1; i <= pow(2.0, k); i++){for (j = 1; j <=pow(2.0,k); j++){printf("%5d", a[i][j]);}printf("\n");}printf("非递归算法消耗的时间为:%d\n", finish - start);printf("这是递归算法:\n");start = (unsigned long)GetCyCount();GameTable2(1, (int)pow(2.0, k));finish = (unsigned long)GetCyCount();for (int i = 1; i <= pow(2.0, k); i++){printf("第");printf("%d", i);printf("天");}printf("\n");for (i = 1; i <= pow(2.0, k); i++){for (j = 1; j <= pow(2.0, k); j++){printf("%5d", a[i][j]);}printf("\n");}printf("递归算法消耗的时间为:%d\n", finish - start);getchar();getchar();getchar();}

🎁总结：理解分治法的精髓，即如何分？如何治？才能使得算法效率更高
👌 作者算是一名Java初学者，文章如有错误，欢迎评论私信指正，一起学习~~
😊如果文章对小伙伴们来说有用的话，点赞👍关注🔎收藏🍔就是我的最大动力！
🚩不积跬步，无以至千里，书接下回，欢迎再见🌹