微分几何I

微分几何I——度量、标架

\quad\quad在Guass 关于内蕴几何研究的启发下，Riemann认识到作为几何学的基本假设，应当将拓扑性质和空间度量性质区别开来，Riemann、Levi、Civita等人在Riemann度量的发展起到重要作用，Riemann提出为每条曲线提供长度的方法，首先为流形上的切向量指定长度，然后沿着曲线积分来定义曲线长度。在Riemman几何中，Levi-Civita平行移动的概念提出对几何发展起到重要作用。它发展为后续的联络以及向量丛上的联络。
在向量空间V中，考虑函数⟨⋅,⋅⟩:V×V⟶R\langle \cdot , \cdot\rangle:V\times V \longrightarrow \mathbb{R}，如果它满足下面两个条件就称为向量V的内积
1. 对称性 ：⟨u,v⟩=⟨v,u⟩，∀u,v∈V\langle u,v\rangle=\langle v,u\rangle，\forall u ,v \in V
2. 非负性：⟨u,u⟩≥0,∀u∈V\langle u,u\rangle \geq 0,\forall u \in V，等号成立当且仅当u=0u=0

内积的作用就是可以定义长度、角度，有了长度角度应用叉积可以定义面积，它可以把欧式空间长度推广至曲面上，接着我们可以定义RIemann度量。从Riemann 度量从发 定义联络然后是 曲率

定义：设MM是mm维光滑流形，gg是MM上的二阶协变张量场或者称(0，2)(0，2)型张量场，如果gg是对称，正定的，称gg是MM上的一个Rimann度量。指定了Riemman度量的光滑流形MM，称为Riemann流形\bf Riemann流形，记为(M,g)(M,g),简记为MM。

假设正则曲线方程为r=r(s)r=r(s)，切向量drd{\bf r}的长度按内积定义
|dr|g=√⟨dr,dr⟩\left|d{\bf r} \right |_g=\sqrt{\langle d{\bf r},d{\bf r}\rangle}
有了长度在定义切向量之间的角度：
θ=arccos(⟨dr,δr⟩|dr|g⋅|δr|g)\theta=arccos \left (\frac {\langle d{\bf r},\delta r \rangle}{\left|d{\bf r} \right |_g \cdot \left|\delta{\bf r} \right |_g}\right)

图1 曲面参数

设曲面Σ\Sigma的参数方程为r(u,v)=(x(u,v),y(u,v),z(u,v)){\bf r}(u,v)=(x(u,v),y(u,v),z(u,v))，则坐标u,vu,v的切向量为
∂r∂u=(∂x∂u,∂y∂u,∂z∂u),∂r∂v=(∂x∂v,∂y∂v,∂z∂v)\frac {\partial {\bf r}}{\partial u}=\left (\frac {\partial {x}}{\partial u},\frac {\partial {y}}{\partial u},\frac {\partial {z}}{\partial u}\right) ,\frac {\partial {\bf r}}{\partial v}=\left (\frac {\partial {x}}{\partial v},\frac {\partial {y}}{\partial v},\frac {\partial {z}}{\partial v}\right)

如果处处有∂x∂v×∂x∂v≠0\frac{\partial {x}}{\partial v}\times\frac{\partial {x}}{\partial v}\neq0，则称Σ\Sigma为正则曲面\bf正则曲面。

图2 曲面参数

切向量dr=(∂r∂udu,∂r∂vdv)=(rudu，rvdv){\bf d{\bf r}=\left(\frac {\partial {\bf r}}{\partial u}d{\bf u},\frac {\partial {\bf r}}{\partial v}d{\bf v} \right)=({\bf r}_udu，{\bf r}_vdv})
法向量n=ru×rv|ru×rv|{\bf n}=\frac {{\bf r}_u\times{\bf r}_v }{\left |{\bf r}_u\times{\bf r}_v\right|}

通过叉积使用长度、角度定义微元面积
dA=|rudu×rvdv|g=|ru|⋅|ru|sin(θ)dudv=√r2ur2v(1−cos2(θ))dudv=√r2ur2v−(ru⋅rv)2dudv=√EG−F2dudvdA=\left|{\bf r}_ud_u\times {\bf r}_vd_v\right |_g=\left|{\bf r}_u\right| \cdot \left|{\bf r}_u\right| sin(\theta) dudv\\=\sqrt{ {\bf r}_u^2{\bf r}_v^2(1-cos^2(\theta))}dudv\\=\sqrt{ {\bf r}_u^2{\bf r}_v^2-({\bf r}_u \cdot {\bf r}_v)^2}dudv\\=\sqrt{EG-F^2}dudv

定义第一基本形式：
I=d{\bf r^2}\\={\langle d{\bf r},d{\bf r}\rangle}={\langle( {\bf r}_udu+{\bf r}_vdv), ({\bf r}_udu+{\bf r}_vdv)\rangle} \\={{\bf r}_u \cdot {\bf r}_ududu+2 {\bf r}_u \cdot {\bf r}_v dudv+{\bf r}_v \cdot {\bf r}_vdvdv}\\=Edu^2+2Fdudv+Gdu^2 I=d{\bf r^2}\\={\langle d{\bf r},d{\bf r}\rangle}={\langle( {\bf r}_udu+{\bf r}_vdv), ({\bf r}_udu+{\bf r}_vdv)\rangle}\\={{\bf r}_u \cdot {\bf r}_ududu+2 {\bf r}_u \cdot {\bf r}_v dudv+{\bf r}_v \cdot {\bf r}_vdvdv}\\=Edu^2+2Fdudv+Gdu^2
这是一个关于du,dv的二次型，整理成矩阵形式：
I= \begin{bmatrix} du & dv \\ \end{bmatrix} \cdot \begin{bmatrix}E &F \\F & G \\ \end{bmatrix} \cdot \begin{bmatrix} du \\dv\\\end{bmatrix}I= \begin{bmatrix} du & dv \\ \end{bmatrix} \cdot\begin{bmatrix}E &F \\F & G \\ \end{bmatrix} \cdot \begin{bmatrix} du \\dv\\\end{bmatrix}

记
g=\begin{bmatrix}E &F \\F & G \\ \end{bmatrix} g=\begin{bmatrix}E &F \\F & G \\ \end{bmatrix}
gg称为度量矩阵。上述计算的微元面积可简化为：
dA=\sqrt {det(g)}dudvdA=\sqrt {det(g)}dudv

考虑微分流形M上的两个开集A,BA,B，如下图所示，它满足AA,BB相交非空，设AA的局部坐标为(x,y)(x,y)度量为\rho\rho；BB的局部坐标是(u,v)(u,v)，度量为gg。它们满足坐标变换。h:(x,y) \rightarrow (u,v)h:(x,y) \rightarrow (u,v)，相应地微分形式满足变换:
\begin{bmatrix} du \\dv\\\end{bmatrix}=\begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix} \begin{bmatrix} du \\dv\\\end{bmatrix}=\begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}

图3 流形M上的坐标变换

在AA与BB相交的区域，它的基本形式I不依赖于坐标选取，所以有：
\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} du & dv\\\end{bmatrix}\cdot g \cdot \begin{bmatrix} du \\dv\\\end{bmatrix} \begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} du & dv\\\end{bmatrix}\cdot g \cdot \begin{bmatrix} du \\dv\\\end{bmatrix}
进一步把微分形式变换带入就有：
\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} ^T \cdot g \cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix}\cdot \begin{bmatrix} dx \\dy\\\end{bmatrix} \begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} ^T \cdot g \cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix}\cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}
所以\rho= \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} ^T \cdot g \cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix}\rho= \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix} ^T \cdot g \cdot \begin{bmatrix}u_x &u_y \\v_x & v_y \\ \end{bmatrix}
满足上述形式的度量称为在曲面上指定了Riemann 度量。

图4 向量内积

文中开头就介绍了内积定义，那是公理化的定义，现在考虑Riemann度量g定义的内积,假设某点的两个向量为d{\bf r},\delta {\bf r}d{\bf r},\delta {\bf r}，则d{\bf r}=(dx,dy)d{\bf r}=(dx,dy)，\delta{\bf r}=(\delta x,\delta y)\delta{\bf r}=(\delta x,\delta y)
它们的内积表示为：
\langle d{\bf r},\delta {\bf r}\rangle=\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} \delta x \\\delta y\\\end{bmatrix}\langle d{\bf r},\delta {\bf r}\rangle=\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot\rho \cdot \begin{bmatrix} \delta x \\\delta y\\\end{bmatrix}

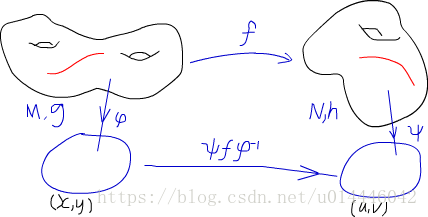
图5 拉回度量

考虑两个Riemann流形(M,g)(M,g),(N,h)(N,h)，\phi,\psi\phi,\psi分别表示两个流形的局部坐标，MM上的曲线通过ff映射到NN上，由于在NN上有相应的度量，它可以定义NN上的长度，这个长度然后拉回到MM上，认为是MM上的长度。角度也类似。如此就在原MM上定义新的度量f^*hf^*h，称为拉回度量。
微分形式从M映射到N ： (dx,dy)\rightarrow(du,dv)(dx,dy)\rightarrow(du,dv)。拉回度量的内积不变
\begin{bmatrix} dx & dy\\\end{bmatrix}\cdot f^*h \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} du & dv\\\end{bmatrix}\cdot h \cdot \begin{bmatrix} du \\dv\\\end{bmatrix} \begin{bmatrix} dx & dy\\\end{bmatrix}\cdot f^*h \cdot \begin{bmatrix} dx \\dy\\\end{bmatrix}=\begin{bmatrix} du & dv\\\end{bmatrix}\cdot h \cdot \begin{bmatrix} du \\dv\\\end{bmatrix}
可得到f^*h=\left(\frac{\partial (u,v)}{\partial (x,y)}\right)^T\cdot h\cdot \left(\frac{\partial (u,v)}{\partial (x,y)}\right)f^*h=\left(\frac{\partial (u,v)}{\partial (x,y)}\right)^T\cdot h\cdot \left(\frac{\partial (u,v)}{\partial (x,y)}\right)
如果拉回度量与原度量相等f^*h=gf^*h=g,则ff是等距变换，若拉回度量与原度量相差一个标量函数f^*h=e^{2 \lambda}gf^*h=e^{2 \lambda}g，\lambda:S\rightarrow\mathbb{R}\lambda:S\rightarrow\mathbb{R}是曲面到\mathbb{R}\mathbb{R}，则ff称为共形变换。

\quad\quad\quad\quad微分几何的出发点是微积分，一条曲线的切线和微分是同一概念，一条封闭曲线包围的面积相当于对其内部积分。微积分在几何上应用主要是曲线和曲面。首先考虑空间正则曲线\Gamma\Gamma，可以认为它是曲面\Sigma\Sigma上的曲线嵌入在欧式\mathbb{R^3}\mathbb{R^3}中，曲线参数方程r=r(s)r=r(s),ss是其弧长参数。对参数方程求导，令{\bf T}(s)=r'(s){\bf T}(s)=r'(s)，则{\bf T}(s){\bf T}(s)是曲线的切向量(tangent vector)。为了描述曲线的弯曲程度，常常使用曲率的概念，它是切向量对弧长的导数d{\bf T}(s)/dsd{\bf T}(s)/ds，记为\kappa(s)\kappa(s)。即：
{\kappa(s)}=\dfrac{d{\bf T}(s)}{ds}{\kappa(s)}=\dfrac{d{\bf T}(s)}{ds}
对于单位切向量\left|{\bf T}(s)\right|=1\left|{\bf T}(s)\right|=1，取平方求导可得，{\bf T'}(s){\bf T}(s){\bf T'}(s){\bf T}(s)=0，由此可以得出{\bf T'}(s){\bf T'}(s)与{\bf T}(s){\bf T}(s)垂直。定义{\bf T'}(s){\bf T'}(s)单位向量为{\bf N}(s){\bf N}(s)，它表示曲线\Gamma\Gamma的主法向量。有了{\bf T}(s),{\bf N}(s){\bf T}(s),{\bf N}(s)这两个向量，可以确定唯一的第2法向量，即：
{{\bf B}(s)}={\bf T}(s)\times{\bf N}(s){{\bf B}(s)}={\bf T}(s)\times{\bf N}(s)
这样{\{r(s),{\bf T}(s),{\bf N}(s),{\bf B}(s)}\}{\{r(s),{\bf T}(s),{\bf N}(s),{\bf B}(s)}\}构成曲线r(s)r(s)的正交标架。

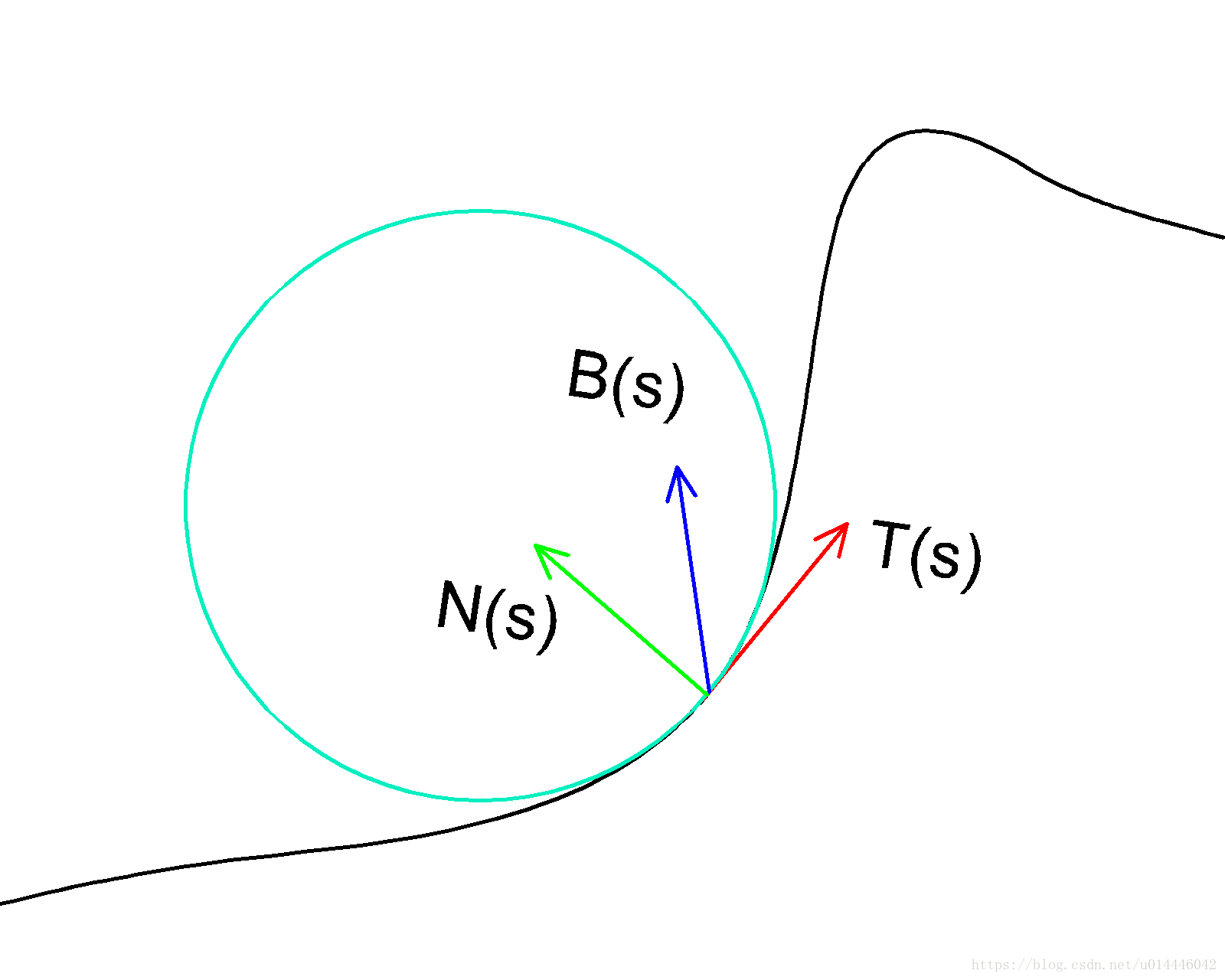
图6 曲线标架

\quad曲线在一点的切线和主法线所张的平面是曲线的密切平面，它的法向量是曲线在p点的次法向量{\bf B}{\bf B}。前面说过，曲线单位切向量{\bf T}{\bf T}关于ss的导数的长度表示曲线的曲率，反映的是曲线的切线方向转动的快慢；类似的是，次法向量关于ss的导数，反映出曲线的密切平面方向转动的快慢，因而它刻画了曲线偏离平面曲线的程度，即曲线的“挠率”。
由于{\{{\bf T}(s),{\bf N}(s),{\bf B}(s)}\}{\{{\bf T}(s),{\bf N}(s),{\bf B}(s)}\}分别是单位切向量、单位主法向量、单位次法向量，和前面类似,
{\bf B'} \bot {\bf B}{\bf B'} \bot {\bf B}，此外，{\bf B}(s)={\bf T}(s)\times{\bf N}(s){\bf B}(s)={\bf T}(s)\times{\bf N}(s)，{\bf T'}(s) \parallel {\bf N}(s){\bf T'}(s) \parallel {\bf N}(s)
对{\bf B}(s){\bf B}(s)求导可得：
{\bf B'}(s)={\bf T'}(s)\times{\bf N}(s)+{\bf T}(s)\times{\bf N'}(s)={\bf T}(s)\times{\bf N'}(s){\bf B'}(s)={\bf T'}(s)\times{\bf N}(s)+{\bf T}(s)\times{\bf N'}(s)={\bf T}(s)\times{\bf N'}(s)
所以{\bf B'} \bot {\bf T}{\bf B'} \bot {\bf T}，{\bf B'}{\bf B'}和{\bf N}{\bf N}共线，既然共形两者相差一个常数，不妨设{\bf B'}=- \tau(s) {\bf N}(s){\bf B'}=- \tau(s) {\bf N}(s)
先前已有 {\bf N}(s){\bf N}(s)是单位向量，上式两边同乘以 {\bf N}(s) {\bf N}(s)可得：
\tau(s)=-{\bf B'} (s){\bf N}(s) \tau(s)=-{\bf B'} (s){\bf N}(s)
这里插一个定义：设 {\bf N}(s){\bf N}(s)和 {\bf B}(s){\bf B}(s)分别是曲线C的主法向量和次法向量，其中ss是曲线的弧长参数，则 \tau(s)=-{\bf B'} (s){\bf N}(s) \tau(s)=-{\bf B'} (s){\bf N}(s)称为曲线C的挠率。

有了这些曲率、挠率、标架后我们可以推出曲线运动公式
\begin{align} {\bf T}(s) & = r'(s) &\text{切向量} \tag 1\\ {\bf T'}(s) & =\kappa(s){\bf N}(s)& \text{曲率} \tag 2\\ {\bf B'}(s) & = -\tau(s){\bf N}(s) & \text{挠率} \tag 3\\ \end{align}\begin{align} {\bf T}(s) & = r'(s) &\text{切向量} \tag 1\\ {\bf T'}(s) & =\kappa(s){\bf N}(s)& \text{曲率} \tag 2\\ {\bf B'}(s) & = -\tau(s){\bf N}(s) & \text{挠率} \tag 3\\\end{align}

要使用运动公式，上述还缺{\bf N'}(s) {\bf N'}(s) ，由右手法则可知：
{\bf N}(s) ={\bf B}(s)\times{\bf T}(s){\bf N}(s) ={\bf B}(s)\times{\bf T}(s)
两边微分：
\begin{align} {\bf N}'(s) & = B'(s) \times T(s)+B(s) \times T'(s) \tag 1\\ & = -\tau(s)N(s)\times T(s)+B(s)\times\kappa(s)N(s) \tag2 \\ & =-\tau(s)\times(-B(s))+\kappa(s)\times(-T(s)) \tag 3\\ & =\tau(s)B(s)-\kappa(s)T(s)\tag4 \end{align}\begin{align}{\bf N}'(s) & = B'(s) \times T(s)+B(s) \times T'(s) \tag 1\\ & = -\tau(s)N(s)\times T(s)+B(s)\times\kappa(s)N(s) \tag2 \\ & =-\tau(s)\times(-B(s))+\kappa(s)\times(-T(s)) \tag 3\\ & =\tau(s)B(s)-\kappa(s)T(s)\tag4\end{align}

如果整理成矩阵形式：
\begin{bmatrix} {\bf T'}(s) \\ {\bf N'}(s)\\ {\bf B'}(s) \\ \end{bmatrix} = \begin{bmatrix}0 & \kappa(s) & 0 \\-\kappa(s) & 0 & \tau(s) \\0 & -\tau(s) & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf T}(s) \\ {\bf N}(s)\\ {\bf B}(s) \\ \end{bmatrix} \begin{bmatrix} {\bf T'}(s) \\ {\bf N'}(s)\\ {\bf B'}(s) \\ \end{bmatrix} =\begin{bmatrix}0 & \kappa(s) & 0 \\-\kappa(s) & 0 & \tau(s) \\0 & -\tau(s) & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf T}(s) \\ {\bf N}(s)\\ {\bf B}(s) \\ \end{bmatrix}
这个公式称为Frenet公式。

考虑曲面\Sigma\Sigma的参数方程r(u,v)r(u,v)，定义e_1e_1是曲面S的单位切向量场，在切平面上将e_1e_1逆时针旋转90^\circ 90^\circ 得到e_2e_2，e_1\times e_2e_1\times e_2得到e_3e_3向量场。\{r(u,v),e_1(u,v),e_2(u,v),e_3(u,v)\}\{r(u,v),e_1(u,v),e_2(u,v),e_3(u,v)\}构成曲面的局部标架场

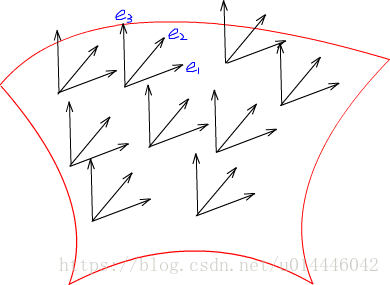
图7 标架场

由微分1形式在切平面上分解
d\mathbb{r}=\mathbb{r}_udu+\mathbb{r}_vdv\\= (\langle\mathbb{r}_u,e_1\rangle e_1+\langle\mathbb{r}_u,e_2\rangle) e_2)du\\+(\langle\mathbb{r}_v,e_1\rangle e_1+\langle\mathbb{r}_v,e_2\rangle) e_2)dv\\= (\langle\mathbb{r}_u,e_1\rangle du+\langle\mathbb{r}_v,e_1\rangle) dv)e_1\\+ (\langle\mathbb{r}_u,e_2\rangle du+\langle\mathbb{r}_v,e_2\rangle) dv)e_2\\=\omega_1e_1+\omega_2e_2d\mathbb{r}=\mathbb{r}_udu+\mathbb{r}_vdv\\=(\langle\mathbb{r}_u,e_1\rangle e_1+\langle\mathbb{r}_u,e_2\rangle) e_2)du\\+(\langle\mathbb{r}_v,e_1\rangle e_1+\langle\mathbb{r}_v,e_2\rangle) e_2)dv\\=(\langle\mathbb{r}_u,e_1\rangle du+\langle\mathbb{r}_v,e_1\rangle) dv)e_1\\+(\langle\mathbb{r}_u,e_2\rangle du+\langle\mathbb{r}_v,e_2\rangle) dv)e_2\\=\omega_1e_1+\omega_2e_2
构成微分形式分解。
同理切向量存在分解：de_i=\omega_{i1}e_1+\omega_{i2}e_2+\omega_{i3}e_3de_i=\omega_{i1}e_1+\omega_{i2}e_2+\omega_{i3}e_3
\langle e_i,e_j\rangle=\delta^i_j \implies \langle de_i,e_j\rangle+\langle e_i,de_j\rangle=0$ \implies \omega_{ij}+\omega_{ji}=0\langle e_i,e_j\rangle=\delta^i_j \implies \langle de_i,e_j\rangle+\langle e_i,de_j\rangle=0$ \implies \omega_{ij}+\omega_{ji}=0
曲面标架运动方程：
d\mathbb{r}=\mathbb{r}_udu+\mathbb{r}_vdv=\omega_1e_1+\omega_2e_2d\mathbb{r}=\mathbb{r}_udu+\mathbb{r}_vdv=\omega_1e_1+\omega_2e_2
d \begin{bmatrix} {{\bf e}_1} \\ {\bf e}_2\\ {\bf e}_3\\ \end{bmatrix} = \begin{bmatrix}0 & \omega_{12} & \omega_{13} \\-\omega_{12} & 0 &\omega_{23} \\-\omega_{13} & -\omega_{23} & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf e}_1 \\ {\bf e}_2\\ {\bf e}_3 \\ \end{bmatrix}d \begin{bmatrix} {{\bf e}_1} \\ {\bf e}_2\\ {\bf e}_3\\ \end{bmatrix} =\begin{bmatrix}0 & \omega_{12} & \omega_{13} \\-\omega_{12} & 0 &\omega_{23} \\-\omega_{13} & -\omega_{23} & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf e}_1 \\ {\bf e}_2\\ {\bf e}_3 \\ \end{bmatrix}
有了微分1-形式的公式，后面的几何计算都可以采用微分形式表示，比较方便。也便于联系上同调等。
基本量用微分形式表示：
1.Riemann 度量：\langle d{\bf r},d{\bf r}\rangle=\omega_1^2+\omega_2^2\langle d{\bf r},d{\bf r}\rangle=\omega_1^2+\omega_2^2
2.面元:dA_g=\omega_1 \wedge \omega_2dA_g=\omega_1 \wedge \omega_2
3.联络：\omega_{12}\omega_{12}

联络和平行移动
联络D是为了定义曲面上的切向量的微分而出现的，它与平行移动有关，谈到平行移动首先考虑测地线上的平行移动，测地线是曲面上两点最短线，曲面SS在点pp处的切向量\vec v_p\vec v_p沿着测地线\gamma(t)\gamma(t)平行移动满足：1.切向量\vec v_p\vec v_p和该点处的测地线的切向量\gamma'(0) \gamma'(0) 保持夹角不变；2.切向量\vec v_p\vec v_p模长不变；3.\vec v_p \in T_p^*S\vec v_p \in T_p^*S。对于普通曲线取曲线上的分点，在分点之间取测地线，这就是分段测地线，让分点取更细，最后取极限，即可得到平行移动。对于欧式空间的平行移动比较简单，因为测地线是线段，平行移动后向量不变，而对于曲面上的平行移动就比较复杂了。从分析上描述平行移动有利于计算，参考欧式的平行移动，曲面的平行移动可以描述为D_{\gamma'(t)}\vec v(t))=0D_{\gamma'(t)}\vec v(t))=0,测地线方程可以描述为D_{\gamma(t)}\vec v(t)=0D_{\gamma(t)}\vec v(t)=0。所以有了联络就可以计算平行移动和测地线了。
定义联络D作用于函数:
D_{\vec v}f=df(\vec v)D_{\vec v}f=df(\vec v)
定义联络D作用于向量:
D_{\vec v}({fe_1+ge_2})=D_{\vec v}({f})e_1+fD_{\vec v}e_1+D_{\vec v}({g})e_2+gD_{\vec v}e_2D_{\vec v}({fe_1+ge_2})=D_{\vec v}({f})e_1+fD_{\vec v}e_1+D_{\vec v}({g})e_2+gD_{\vec v}e_2
其中：
D_{\vec v}({e_1})=\langle De_1, {\vec v}\rangle=\omega_{12}e_2D_{\vec v}({e_1})=\langle De_1, {\vec v}\rangle=\omega_{12}e_2
D_{\vec v}({e_2})=\langle De_2, {\vec v}\rangle=-\omega_{12}e_1D_{\vec v}({e_2})=\langle De_2, {\vec v}\rangle=-\omega_{12}e_1

仿照曲面运动方程
D_\vec v \begin{bmatrix} {{\bf e}_1} \\ {\bf e}_2\\ {\bf e}_3\\ \end{bmatrix} = \begin{bmatrix}0 & \omega_{12} & 0 \\-\omega_{12} & 0 &0 \\0 & 0 & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf e}_1 \\ {\bf e}_2\\ {\bf e}_3 \\ \end{bmatrix}D_\vec v \begin{bmatrix} {{\bf e}_1} \\ {\bf e}_2\\ {\bf e}_3\\ \end{bmatrix} =\begin{bmatrix}0 & \omega_{12} & 0 \\-\omega_{12} & 0 &0 \\0 & 0 & 0\\ \end{bmatrix} \cdot \begin{bmatrix} {\bf e}_1 \\ {\bf e}_2\\ {\bf e}_3 \\ \end{bmatrix}

有了上述公式后续的计算就可以进行了。

参考文献：
1.顾险峰，计算共形几何讲义，高等教育出版社，2008
2.陈省身，微分几何，世界图书出版公司，2006
3.陈维桓，微分几何，北京大学出版社，2006