人工鱼群算法及其python实现过程
得益于仿生学的研究和发展，群智能优化领域近年来衍生出了多种细化的方法，包括遗传算法、粒子群优化算法(附代码)、杂草算法(附代码)、果蝇算法以及人工鱼群算法。其中，李晓磊博士于2003年提出的鱼群算法具有避免最优解提前收敛即能够跳出局部最优解而寻求全局最优解的优点。
0 自然界中的鱼群特征
捕食行为：鱼向着生存环境中富集度高的地方游去并捕食。
追尾行为：鱼A能够察觉视线范围内鱼B所处的富集度最高，若鱼B周围不太拥挤，那么鱼A朝着鱼B游去。
聚群行为：鱼找到视线范围内所有的鱼，并能够衡量这些鱼的中间位置，如果这个中间位置不是很拥挤，那么鱼朝着中间位置游去
随机行为：鱼在当前环境中随机游动
1 人工鱼群算法
1.0 初始化鱼群及算法参数
div-----------------解的自变量个数。 e.g: div = 3 --> X = x1, x2, x3
number----------自变量向量
visual-------------鱼群视觉范围
step---------------鱼移动一步的最大步长
try_time----------鱼进行捕食行为时搜索周围环境更优解的次数
delta--------------拥挤程度，[0, 1)，影响追尾和聚群
tag----------------公告牌，记录每次循环过后，目标函数的最优值
1.1 进入循环，鱼群中的鱼分别进行如下操作：(伪代码如下)
捕食行为
def prey()pre_score = fish.func() # 原来fish的目标函数值for(i in 0 : try_time) newfish = new Fish(rnorm(fish.number, sigma)) # 以fish为中心生成新的new_fishif(newfish.func() > pre_score) # 产生了更优解fish = new_fish追尾行为
def follow()fo = 鱼fish视线范围内所有鱼的集合best_fish = fo集合中目标函数值最高的鱼if(best_fish周围拥挤)执行其他操作，如捕食行为、随机行为elsefish向best_fish移动，最大移动距离为step聚群行为
def swarm()sw = 鱼fish视线范围内所有鱼的集合center_fish = sw的中心位置if(center_fish周围拥挤)执行其他行为，如随机操作、捕食操作elsefish向center_fish移动，最大移动step长随机行为
def rand() 以当前fish位置为中心，随机向四周移动，每个维度上最多移动step长2 python实现过程
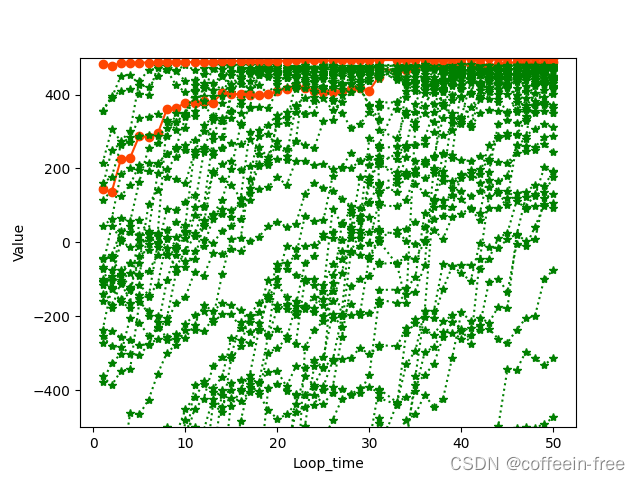
import mathimport matplotlib.pyplot as pltimport numpymy_flag = 1# my_flag == 0 计算第一个函数最大值# my_flag == 1 计算第二个函数最大值class fish: def __init__(self, div, number, visual, step, try_time, delta): # 初始化 self.div = div self.number = number self.visual = visual self.step = step self.try_time = try_time self.delta = delta def distance(self, f): # 计算self鱼和f鱼之间的距离 ll = len(self.number) res = 0.0 for i in range(ll): res = res + (self.number[i] - f.number[i]) * (self.number[i] - f.number[i]) return math.sqrt(res) def func(self, flag): # 计算鱼在当前位置的函数 ll = len(self.number) if flag == 0: res = 0 for i in range(ll): res = res + self.number[i] * self.number[i] return 500-res else: res = 0 mul = 1 for i in range(ll): res = res + math.fabs(self.number[i]) mul = mul * math.fabs(self.number[i]) return 500-(res + mul) def prey(self): # 捕食操作 pre = self.func(my_flag) for i in range(self.try_time): rand = numpy.random.randint(-99, 99, self.div) / 100 * self.visual for j in range(self.div): self.number[j] = self.number[j] + rand[j] cur = self.func(my_flag) if cur > pre: # 捕食成功 # print('原始分数：' + str(pre) + '新分数：' + str(cur) + '捕食成功！！') return cur else: # 捕食失败 for j in range(self.div): self.number[j] = self.number[j] - rand[j] # print("捕食失败！") return pre def swarm(self, fishes): # 聚群行为：向视觉内鱼群中心前进step close_swarm = find_close_swarm(fishes, self) center_f = center_fish(close_swarm) n = len(close_swarm) - 1 if n != 0 and (center_f.func(my_flag) / n > self.delta * self.func(my_flag)): # print("聚群运动") for i in range(self.div): self.number[i] = self.number[i] + self.step * center_f.number[i] return self.func(my_flag) else: # print("随机运动") return self.rand() def rand(self): for i in range(self.div): self.number[i] = self.number[i] + self.step * numpy.random.uniform(-1, 1, 1) def follow(self, fishes): # 追尾行为：向着视觉内鱼群中目标函数值最优的鱼前进step close_swarm = find_close_swarm(fishes, self) best_f = best_fish(close_swarm) n = len(close_swarm) - 1 if n != 0 and (best_f.func(my_flag) / n > self.delta * self.func(my_flag)): # 向前移动 # print("向前移动") for i in range(self.div): self.number[i] = self.number[i] + self.step * (best_f.number[i] - self.number[i]) return self.func(my_flag) else: # 随机运动 # print("随机运动") return self.rand()def find_close_swarm(fishes, fish_): # 在种群fishes中查找fish_视觉范围内的鱼 # 输入为fishes，是一个list型变量 和一个fish对象 # 输出为一个fish list res = [] for fi in fishes: if fish_.distance(fi) < fish_.visual: res.append(fi) return resdef center_fish(fishes): # 计算当前种群的中心位置，并将其中心位置记为certer_fish以完成聚群操作 # 输入为fishes，是一个list型变量 # 输出为一个fish对象 ll = len(fishes) if ll == 0 or ll == 1: return None res = fish(fishes[0].div, fishes[0].number, fishes[0].visual, fishes[0].step, fishes[0].try_time, fishes[0].delta) for i in range(fishes[0].div): res.number[i] = 0 for i in range(ll): for j in range(res.div): res.number[j] = res.number[j] + fishes[i].number[j] return resdef best_fish(fishes): # 计算当前种群最优个体的位置，并将其返回用于追尾操作 # 输入为fishes，是一个list型变量 # 输出为一个fish对象 ll = len(fishes) if ll == 0 or ll == 1: return None index = -1 max = 0 for i in range(ll): if index == -1 or max < fishes[i].func(my_flag): index = i max = fishes[i].func(my_flag) return fishes[index]def main(): # 主函数 fishes = [] div = 3 # xi中i的大小，e.g. div == 3 --> x1, x2, x3 fish_num = 50 # 鱼群个体数目 gmax = 100 # 循环最大次数 tag = 0 # 公告牌 visual = 1 step = 0.2 try_time = 10 delta = 0.3 list_of_fishes = [] # 初始化鱼群 for i in range(fish_num): num = numpy.random.uniform(10, 20, div) fi = fish(div, num, visual, step, try_time, delta) fishes.append(fi) for i in range(fish_num): list_of_fishes.append([]) for g in range(gmax): for i in range(fish_num): if fishes[i].func(my_flag) > tag: tag = fishes[i].func(my_flag) # print(g, tag) for i in range(fish_num): if g >= 50: list_of_fishes[i].append(fishes[i].func(my_flag)) for i in range(fish_num): if tag == fishes[i].func(my_flag): fishes[i].prey() continue tmp = numpy.random.randint(0, 3, 1) if tmp == 0: fishes[i].swarm(fishes) elif tmp == 1: fishes[i].follow(fishes) else: fishes[i].prey() print(tag) x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 31, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50] # print(x) for i in range(fish_num): # print(list_of_fishes[i][49] < 0.5) if math.fabs(list_of_fishes[i][49] - 500) < 20: plt.plot(x, list_of_fishes[i], color='orangered', marker='o', linestyle='-', label='A') else: plt.plot(x, list_of_fishes[i], color='green', marker='*', linestyle=':', label='C') plt.ylim(20, 50) plt.ylim(-500, 500) plt.xlabel("Loop_time") # X轴标签 plt.ylabel("Value") # Y轴标签 plt.show()if __name__ == '__main__': main()3 结果展示
目标函数为F(X) = 500 - x1^2 - x2 ^ 2 - x3 ^2
最优解为F(0, 0, 0) = 500 (最大值)
附：
其他群智能优化算法：
粒子群优化算法(附代码)
https://blog.csdn.net/cccddduil/article/details/123671197?spm=1001.2014.3001.5501
杂草算法(附代码)https://blog.csdn.net/cccddduil/article/details/124843486?spm=1001.2014.3001.5502
