约瑟夫环排列问题
别把自己太当回事,要把你做的事当回事!💓💓💓
文章目录
-
- 1、问题描述
- 2、问题分析
- 3、分文件源码分析
-
- 1.头文件(Jose.h):
- 2.子函数源文件(Jose.c):
- 3.主函数源文件(test.c):
- 4、整体代码
- 结语
1、问题描述
【问题描述】编号为1,2,3,……,n的n个人按顺时针方向围坐在一张圆桌周围。给定一个正整数m<n,从第一个人开始按顺时针方向自1开始报数,每报到m时就让其出列,且计数继续进行下去。如此下去,直到圆桌周围人全部出列为止。最后出列者为优胜者。每个人的出列次序定义了整数1,2,3,……,n的一个排列。这个排列成为一个(n,m)Josephus排列。例如:若(7,3)Josephus排列为3,6,2,7,5,1,4,对于给定的1,2,3,……,n中的K个数,Josephus想知道是否存在一个正整数m(m<n),使得Josephus(n,m)排列最后k个数恰好为事先指定的k个数。
【基本要求】利用单向循环链表存储结构模拟约瑟夫环过程,按照出列顺序输出各人编号。
【测试数据】
输入数据:n = 7,k = 4,指定排列的最后k个数为7、5、1、4。
输出数据:m =的值为3。
2、问题分析
1、这个问题就是传统约瑟夫环问题的延申,里面存在一些它的逆思维,然后最终求m的值。
2、这里小编提供一种解题思路,因为小编也是处于学习中,所以若存在问题,还请大家批评指正:
(1)首先我们来说说其中的n、k以及m的含义:n在这里就是最初的总人数,k是指定的最后k个数,m是遇到第m个就出列。
(2)其次这里就是和最初的约瑟夫环问题一样,因为在约瑟夫环问题里面m是已知的,而这个约瑟夫环排列里面m是需要求解的,而我们都知道m<n这个条件。因此这里用的方法就是设置循环变量 i ,让其放在m的位置上开始循环,然后判断循环出列的后k个数据和指定的是否一致。
(3)最后,若一致,则直接输出此时 i 的值,即 m 的值。
3、分文件源码分析
1.头文件(Jose.h):
#include #include #include #define N 10extern int brr[N];//在头文件中声明一个全局变量的数组,用来存约瑟夫环里面出列的数typedef int SLDataType;//类型重定义extern struct LNode* Phead;//在头文件中声明一个全局变量用来记录链表的尾结点typedef struct LNode{SLDataType val;struct LNode* next;}LN;LN* BuyLnode(SLDataType x);//创建一个结点void LnodeInit(LN** PPhead, SLDataType n);//实现链表循环void Jose(LN** PPhead, SLDataType n, SLDataType m);//实现排列2.子函数源文件(Jose.c):
#include "Jose.h"struct LNode* Phead;//创建一个结点LN* BuyLnode(SLDataType x){LN* newnode = (LN*)malloc(sizeof(LN));if (newnode == NULL){printf("malloc fail\n");exit(-1);}else{newnode->val = x;newnode->next = NULL;}return newnode;}//实现链表循环void LnodeInit(LN** PPhead, SLDataType n){LN* cur = *PPhead;assert(PPhead);for (int i = 1; i <= n; i++)//创建n个节点成一个链表,并且是链表单向循环{LN* newnode = BuyLnode(i);if (*PPhead == NULL){*PPhead = newnode;}else{//找尾,进行尾插创建多个结点LN* tail = *PPhead;while (tail->next != NULL){tail = tail->next;}tail->next = newnode;if (i == n){cur = tail->next;cur->next = *PPhead;}}}Phead = cur;//将链表尾部结点标记下来,然后让尾部和头部结点一起向下走,//即就能每次保证得到出列结点和出列前一个结点的地址}//实现排列void Jose(LN** PPhead, SLDataType n, SLDataType m){int count = 1, j = 0;LN* cur = *PPhead;LN* prev = *PPhead;assert(PPhead);assert(PPhead);while (prev){count = 1;while (count != m){prev = prev->next;//这就是每次向下移动寻找每次需要出列的结点Phead = Phead->next;//这里就是寻找每次出列结点的上一个结点count++;}cur = prev;brr[j++] = cur->val;//将每次出列的值用数组brr记录下来if (prev == prev->next)//判断只剩下一个节点时候进行置空处理{prev = NULL;}else{Phead->next = prev->next;free(cur);cur = NULL;prev = Phead->next;}}*PPhead = NULL;}3.主函数源文件(test.c):
#include "Jose.h"int brr[N];//定义在该文件使用的全局变量int main(){int arr[N] = { 0 };int n = 0, k = 0;int count = 0, flag = 1;LN* Ps = NULL;printf("n和k的值为:");scanf("%d %d", &n, &k);printf("最后k个数的排列:");for (int i = n - k; i < n; i++){scanf("%d", &arr[i]);}for (int i = 1; i <= n; i++)//这里利用循环从头开始找m的值{Ps = NULL;//每次进循环都需要一个空链表count = 0;LnodeInit(&Ps, n);//然后创建n节结点的链表Jose(&Ps, n, i);for (int j = n - k; j < n; j++)//将给定的后k个数的排列和约瑟夫环输出的后k个值进行比较{if (arr[j] == brr[j]){count++;continue;}}if (count == k)//都相等时候就输出值,并且跳出循环停止再向后寻找{printf("m值为:%d\n", i);break;}}return 0;}4、整体代码
上面是分文件操作的三个文件模块,这里小编也将其稍加放在同一个文件里面:
#include #include #include #define N 10int brr[N];//定义一个全局变量的数组,用来存约瑟夫环里面出列的数typedef int SLDataType;//类型重定义struct LNode* Phead;//定义一个全局变量用来记录链表的尾结点typedef struct LNode{SLDataType val;struct LNode* next;}LN;LN* BuyLnode(SLDataType x);//创建一个结点void LnodeInit(LN** PPhead, SLDataType n);//实现链表循环void Jose(LN** PPhead, SLDataType n, SLDataType m);//实现排列//创建一个结点LN* BuyLnode(SLDataType x){LN* newnode = (LN*)malloc(sizeof(LN));if (newnode == NULL){printf("malloc fail\n");exit(-1);}else{newnode->val = x;newnode->next = NULL;}return newnode;}//实现链表循环void LnodeInit(LN** PPhead, SLDataType n){LN* cur = *PPhead;assert(PPhead);for (int i = 1; i <= n; i++)//创建n个节点成一个链表,并且是链表单向循环{LN* newnode = BuyLnode(i);if (*PPhead == NULL){*PPhead = newnode;}else{//找尾,进行尾插创建多个结点LN* tail = *PPhead;while (tail->next != NULL){tail = tail->next;}tail->next = newnode;if (i == n){cur = tail->next;cur->next = *PPhead;}}}Phead = cur;//将链表尾部结点标记下来,然后让尾部和头部结点一起向下走,//即就能每次保证得到出列结点和出列前一个结点的地址}//实现排列void Jose(LN** PPhead, SLDataType n, SLDataType m){int count = 1, j = 0;LN* cur = *PPhead;LN* prev = *PPhead;assert(PPhead);assert(PPhead);while (prev){count = 1;while (count != m){prev = prev->next;//这就是每次向下移动寻找每次需要出列的结点Phead = Phead->next;//这里就是寻找每次出列结点的上一个结点count++;}cur = prev;brr[j++] = cur->val;//将每次出列的值用数组brr记录下来if (prev == prev->next)//判断只剩下一个节点时候进行置空处理{prev = NULL;}else{Phead->next = prev->next;free(cur);cur = NULL;prev = Phead->next;}}*PPhead = NULL;}int main(){int arr[N] = { 0 };int n = 0, k = 0;int count = 0, flag = 1;LN* Ps = NULL;printf("n和k的值为:");scanf("%d %d", &n, &k);printf("最后k个数的排列:");for (int i = n - k; i < n; i++){scanf("%d", &arr[i]);}for (int i = 1; i <= n; i++)//这里利用循环从头开始找m的值{Ps = NULL;//每次进循环都需要一个空链表count = 0;LnodeInit(&Ps, n);//然后创建n节结点的链表Jose(&Ps, n, i);for (int j = n - k; j < n; j++)//将给定的后k个数的排列和约瑟夫环输出的后k个值进行比较{if (arr[j] == brr[j]){count++;continue;}}if (count == k)//都相等时候就输出值,并且跳出循环停止再向后寻找{printf("m值为:%d\n", i);break;}}return 0;}运行结果:
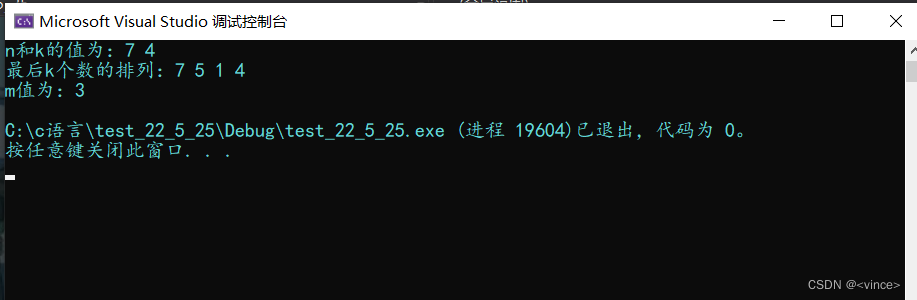
结语
本次小实验是经典的约瑟夫环的变形问题,将其演变成一个排列问题,然后给出部分内部排列,最终求第m个出列的m值。当然还有很多其他的方法,小编在这里就提供一种思路,大家可以参考参考,如有不足之处,还请批评指正。

🎉🎉🎉以上代码均可运行,所用编译环境为 vs2019 ,运行时注意加上编译头文件#define _CRT_SECURE_NO_WARNINGS 1


