双向冒泡排序
1.问题描述:
实现双向冒泡排序。
2.实验要求:
(1)设计待排序记录的存储结构;
(2)设计双向冒泡排序算法;
(3)输入:任意输入n个整数,数据个数和数据由键盘输入;
(4)输出:各趟的排序结果;
3.程序实现:
(1)代码:
#include using namespace std;void swap(int* a, int* b)//交换两个数据元素的值{ int temp = *a; *a = *b; *b = temp;}void print(int arr[], int n);//声明// 冒泡排序(双向)void BidBubbleSort(int arr[], int len){ int left, right, flag, i; int t = 1; int lastchange = 0; left = 0; right = len - 1; // 注意,left和right的初始值,决定了下面for循环中应使用“<”或“”或">="。 while (left < right) { flag = 0; for (i = left; i arr[i + 1]) // 找到剩下中最大的 { swap(&arr[i], &arr[i + 1]); flag = 1; // 标志, 有数据交换 lastchange = i; // 此处lastchange的最终值,就是本轮正向冒泡中,最后一次交换数据的位置。该位置之后的数据都已经排序好了。 } } right = lastchange; cout << "第" << t << "趟排序结果:"; t++; print(arr, len); cout << "交换位置" << lastchange; cout < left; i--) // 反向冒泡 { if (arr[i] < arr[i - 1]) // 找到剩下中最小的 { swap(&arr[i], &arr[i - 1]); flag = 1; lastchange = i; // 此处lastchange的最终值,就是本轮反向冒泡中,最后一次交换数据的位置。该位置之前的数据都已经排序好了。 } } left = lastchange; cout << "第" << t << "趟排序结果:"; t++; print(arr, len); cout << "交换位置" << lastchange; cout << endl; if (!flag)//无数据交换,结束循环 break; }}// 输出void print(int arr[], int n){ for (int i = 0; i < n; i++)cout<<arr[i]<<'\t';}int main(int argc, const char* argv[]) { int arr[100]; int n; cout <> n; cout << "输入待排序列:"; for (int i = 0; i > arr[i]; int len =n; // 排序前数组序列 print(arr, len); cout << '\n'; BidBubbleSort(arr, len); // 排序后数组序列 print(arr, len); return 0;}(2)建立的模型及存储结构:
采用顺序存储的数组存放待排序列。
算法原理:
- 先对数组从左到右进行冒泡排序(升序),则最大的元素去到最右端
- 再对数组从右到左进行冒泡排序(降序),则最小的元素去到最左端
- 以此类推,依次改变冒泡的方向,并不断缩小未排序元素的范围,直到最后一个元素结束
4.测试与运行:
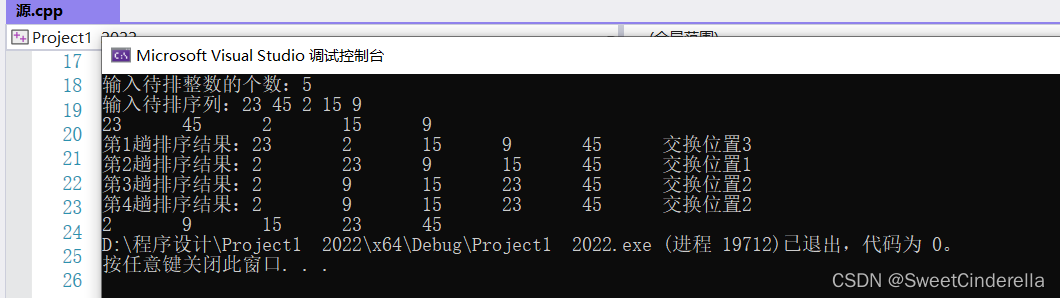
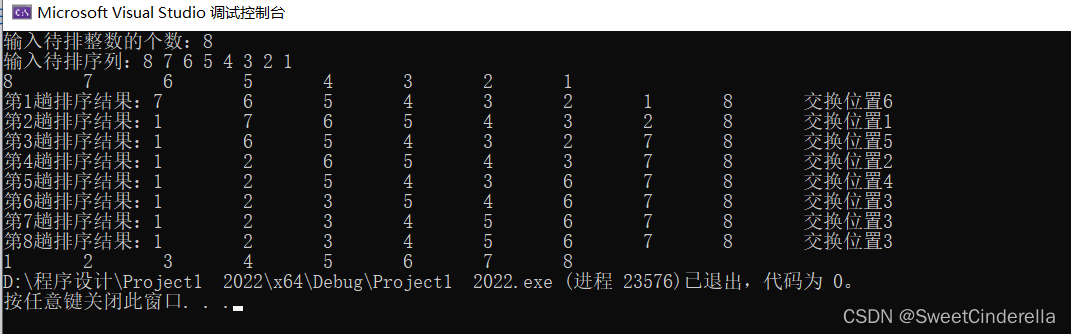
5.思考题
(1)冒泡排序最适合用的情况是正序还是逆序?为什么?
冒泡排序,最好的情况是序列已经是正序,时间复杂度为O(n),最坏的当然是逆序,时间复杂度为O(n^2)。
(2)快速排序是内部排序中平均时间复杂度最好的排序算法之一,在正序的情况下,快速排序的效果会比冒泡好吗?如果不会,那么快速排序什么情况下,是使用它的最好时机?
不会,快速排序在最坏的情况下,待排序的序列为正序或者逆序,每次划分只得到一个比上一次划分少一个记录的子序列,注意另一个为空。如果递归树画出来,它就是一棵斜树。此时需要执行n‐1次递归调用。最终其时间复杂度为O(n^2)。
最优情况下,Partition每次都划分得很均匀,在最优的情况下,快速排序算法的时间复杂度为O(nlogn)。


