二叉树讲解《三》(堆的应用)
个人主页:欢迎大家光临——>沙漠下的胡杨
各位大帅哥,大漂亮
如果觉得文章对自己有帮助
可以一键三连支持博主
你的每一分关心都是我坚持的动力

☄: 本期重点:堆排序以及Topk问题的实现
希望大家每天都心情愉悦的学习工作。
☄: 本期重点:堆排序以及Topk问题的实现
堆排序(基本不使用):
堆排序适用版:
我们有两种建堆方式:
1.向上调整建堆:
2.向下调整建堆:
排升序和降序分别建什么堆呢?
整体代码实现:
堆实现Top-k问题:
解决思路:
模拟实现例子:

在上一篇博客中我们说到了如何实现一个堆,下面我们来用它实现一些功能。
堆排序(基本不使用):
首先我们知道了,位于堆顶的元素是一个堆中最大或者最小的,那么我们可以根据这一特性进行选数,让数据从大到小或者从小到大排序。
根据我们所学的,我们可以先创建堆,然后在把要排序的数组中的元素一个个插入堆中,接着我们在依次取出栈顶元素放入要排序的数组,然后在Pop栈顶元素,循环操作,直到堆为空停止,就排好了。
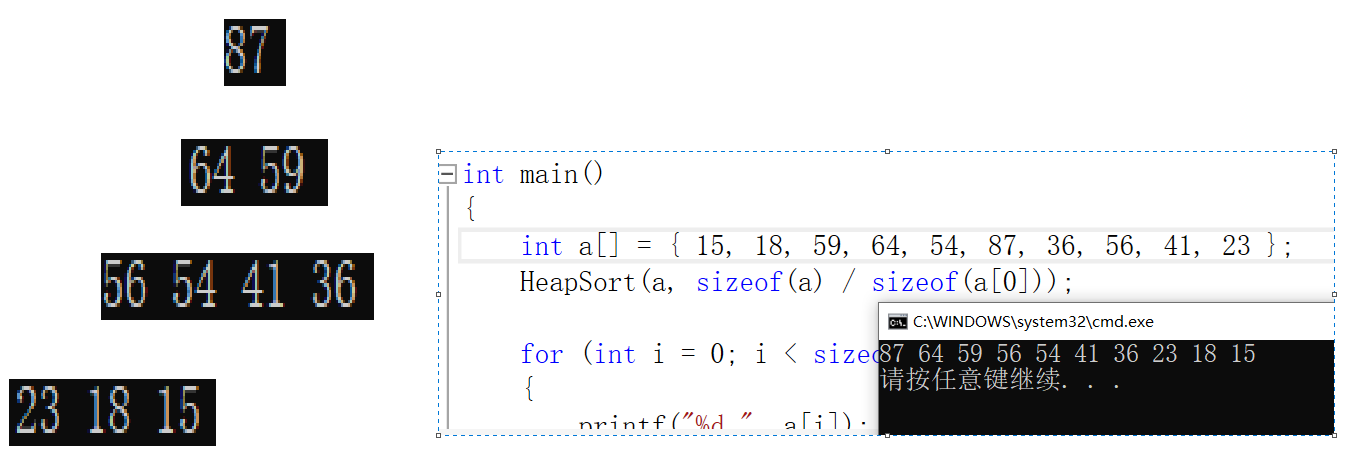
void HeapSort(int *a,int n){HP hp;HeapInit(&hp);for (int i = 0; i < n; ++i){HeapPush(&hp, a[i]);//插入堆}int i = 0;while (!HeapEmpty(&hp))//判空{a[i++] = HeapTop(&hp);//放入要排序的数组。HeapPop(&hp);//删除堆顶}HeapDestroy(&hp);//销毁堆}int main(){int a[] = { 15, 18, 59, 64, 54, 87, 36, 56, 41, 23 };//要排序的数组HeapSort(a, sizeof(a) / sizeof(a[0]));堆排序for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)//打印{printf("%d ", a[i]);}printf("\n");return 0;}下面是打印结果:
我们可以看出,在逻辑上是二叉树。,并且也是降序排列。好像达到我们的要求了,但是还是有很重要的两点,就是这个排序的失败之处
1. 需要先有一个堆 这样的数据结构,才能使用这种办法。
2.在排序过程中,额外开辟了一个数字,空间复杂度为O(N)。
所以这种堆排序很不好,下面我们看一个实用的堆排序。
堆排序适用版:
我们有两种建堆方式:
1.向上调整建堆:
我们知道,在堆中那么多函数接口中,其实最关键的是向上调整和向下调整算法,我们可以只使用这两个函数,就完成建堆,然后在进行排序。
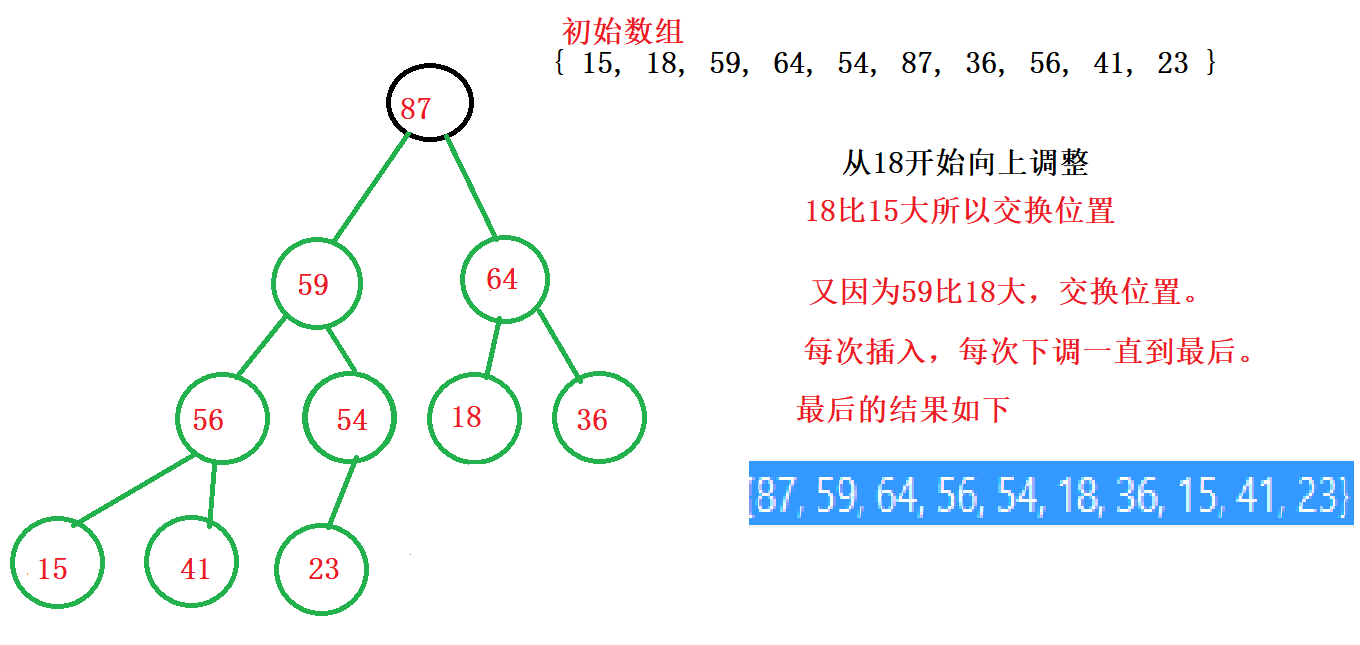
我们调整后就是一个堆了,但是我们如何把这个堆变为有序呢?
我们首先把第一个元素和最后一个元素交换下位置,
我们不考虑最后一个元素,
把第一个元素向下调整,我们就可以得到一个新的堆,
如此反复,就可以得到这个数组的降序。
代码实现如下:
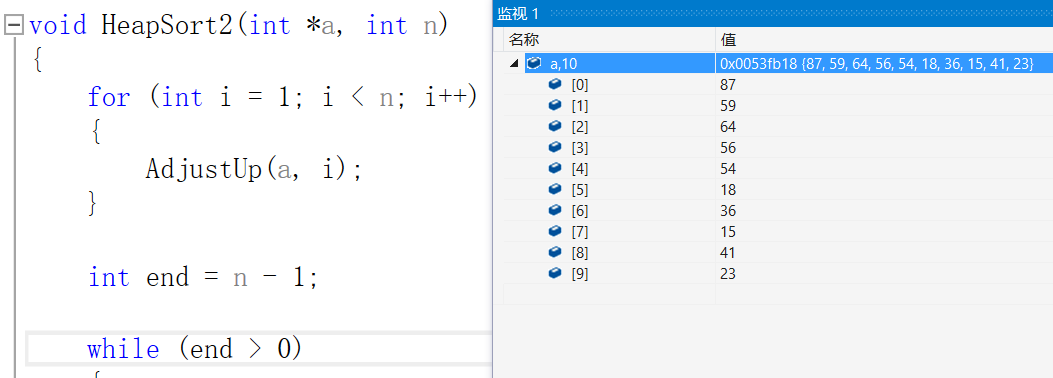
void Swap(HPDataType* p1, HPDataType* p2)//交换{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;}void AdjustDwon(HPDataType* a, int size, int parent)//向下调整{int child = parent * 2 + 1;//左孩子while (child < size)//孩子节点下,到size结束{ //要在确定有右孩子的情况下,右孩子大于左孩子,就使用右孩子(大堆)//想变为小根堆,大于变小于(child +1 <size不变)if (child + 1 < size && a[child] a[parent])//想变为小根堆,大于变小于{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void AdjustUp(HPDataType* a, int child)//向上调整{int parent = (child - 1) / 2;//找到父亲节点while (child > 0)//如果child等于0,表示调整到根,不可在调整返回。{//孩子大于父亲就交换(大根堆)if (a[child] > a[parent])//想变为小根堆,大于变小于{Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}void HeapSort2(int *a, int n){for (int i = 1; i 0){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);--end;}}int main(){int a[] = { 15, 18, 59, 64, 54, 87, 36, 56, 41, 23 };HeapSort2(a, sizeof(a) / sizeof(a[0]));for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++){printf("%d ", a[i]);}printf("\n");return 0;}
2.向下调整建堆:
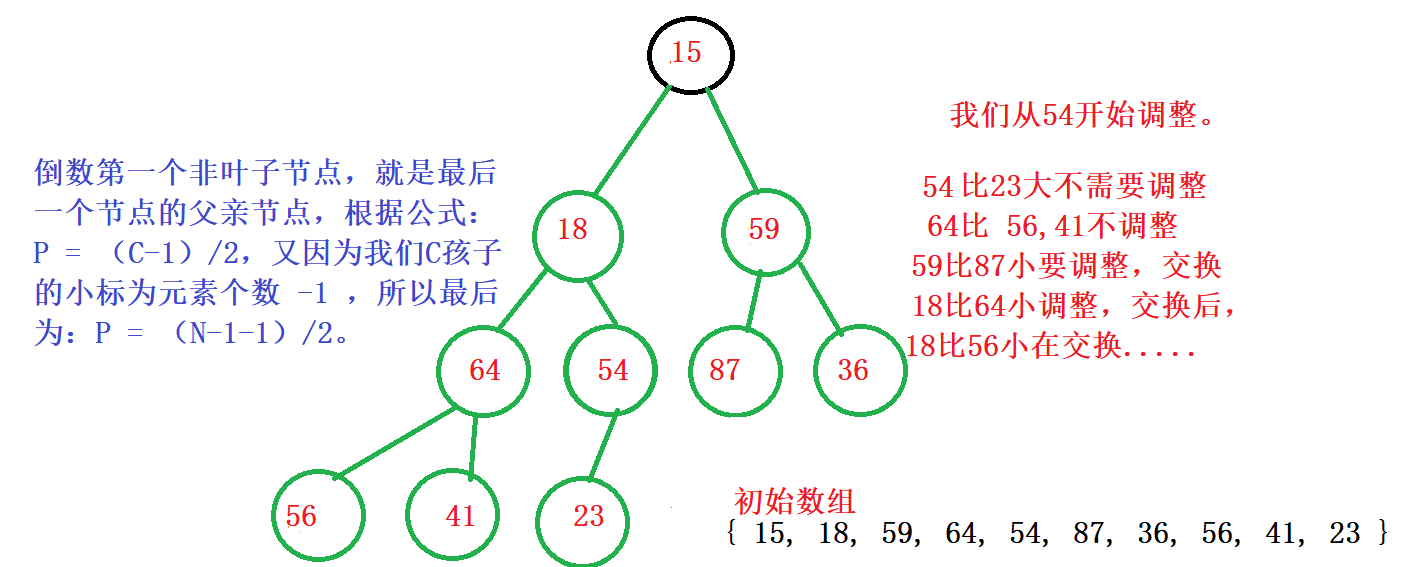
我们向下调整建堆的思路和向上调整不太类似,我们先从倒数第一个非叶子节点向上调整,调整到根结束。
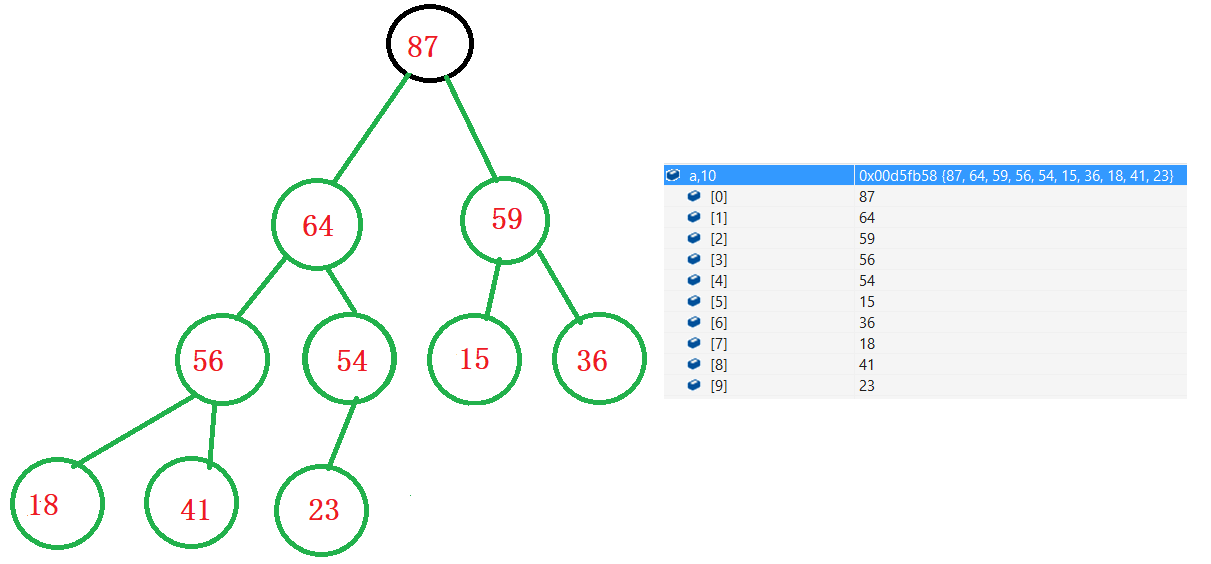
最后我们按照图示方法建堆结果为:
也符合堆的性质,然后后面的思路和向上建堆就一样了,把第一个元素和最后一个元素交换,然后不考虑最后一个元素,让第一个元素向下调整在变为一个堆就好了,重复过程即可
代码如下:
void HeapSort2(int *a, int n){for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDwon(a, n, i);//向下调整建堆}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);--end;}}int main(){int a[] = { 15, 18, 59, 64, 54, 87, 36, 56, 41, 23 };HeapSort2(a, sizeof(a) / sizeof(a[0]));for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++){printf("%d ", a[i]);}printf("\n");return 0;}
排升序和降序分别建什么堆呢?
我们的建堆思路有了,但是我们要把数字排升序和降序分别要建什么堆呢?
排升序,就建大堆,排降序,就建小堆。
解释如下图:
首先,我们是排升序建的大堆,如果我们要排的是降序,我们依然建的大堆,那怎么办?
我们可以找到最大的数据,应该把它放在第一位,然后不考虑它继续找次大的,但是我们的父子关系全乱了,需要重新建堆了,这时间复杂度就变为O(N)*O(N)了,不划算。所以我们选择排降序时建小堆,我们找到其中最小的,然后把最小的放最后,不考虑它,然后使用向下调整,这样时间复杂度就降低为log(N)*O(N),这才是堆排序快的地方。
整体代码实现:
void AdjustDwon(HPDataType* a, int size, int parent)//向下调整{int child = parent * 2 + 1;//左孩子while (child < size)//孩子节点下,到size结束{ //要在确定有右孩子的情况下,右孩子大于左孩子,就使用右孩子(大堆)//想变为小根堆,大于变小于(child +1 <size不变)if (child + 1 < size && a[child] a[parent])//想变为小根堆,大于变小于{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}void AdjustUp(HPDataType* a, int child)//向上调整{int parent = (child - 1) / 2;//找到父亲节点while (child > 0)//如果child等于0,表示调整到根,不可在调整返回。{//孩子大于父亲就交换(大根堆)if (a[child] > a[parent])//想变为小根堆,大于变小于{Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}}void HeapSort2(int *a, int n){ //时间复杂度O(N*logN)//for (int i = 1; i = 0; i--){AdjustDwon(a, n, i);//向下调整建堆}int end = n - 1; //时间复杂度O(N*logN)while (end > 0){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);--end;}}int main(){int a[] = { 15, 18, 59, 64, 54, 87, 36, 56, 41, 23 };HeapSort2(a, sizeof(a) / sizeof(a[0]));for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++){printf("%d ", a[i]);}printf("\n");return 0;}
堆实现Top-k问题:
解决思路:
我们在平时生活中,会遇到很多的类似求前K个最大数的问题,比如我们平时买零食,可能会选销量最好的前十家店购买,然后我们平时打游戏也会有一些实时的排名榜单,这些都是Top-k问题,我们可以使用堆来进行解决。
现在我们遇到了一个问题,让我们从1000亿个数据中选出最大的前1000个数,我们怎么办?
思路1:我们可以使用堆排序,然后取前1000个数据。(空间复杂度太大,不行)
思路2:我们可以建立一个1000元素的小堆,然后使用1000亿中前1000个元素建堆,然后我们从1001个数和堆顶数据比较,如果比他大就进堆,然后向下调整,直到最后一个数据,这个堆就是前1000个大的数据。(空间复杂度很小,时间复杂度偏大一点点,可行)
模拟实现例子:
我们有10000个数,求出最大的前10个数据。我们使用时间戳的概念,用srand函数生成随机数,然后我们对他们取模10000,然后我们在随机给上10个数,把它们的值加上10000,然后判断打印的数据是否大于10000.
代码和运行结果如下:
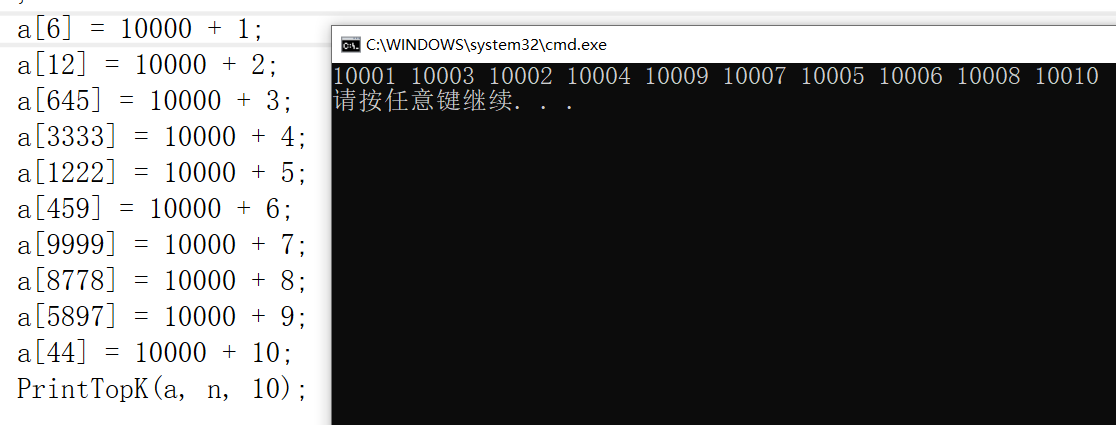
void PrintTopK(int* a, int n, int k){// 1. 建堆--用a中前k个元素建堆int* KMinHeap = (int *)malloc(sizeof(int)*k);assert(KMinHeap);for (int i = 0; i = 0; i--){AdjustDwon(KMinHeap, k, i);}// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换for (int j = k; j KMinHeap[0]){KMinHeap[0] = a[j];AdjustDwon(KMinHeap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", KMinHeap[i]);}printf("\n");}void TestTopk(){int n = 10000;int* a = (int*)malloc(sizeof(int)*n);srand(time(0));for (int i = 0; i < n; ++i){a[i] = rand() % 10000;}a[6] = 10000 + 1;a[12] = 10000 + 2;a[645] = 10000 + 3;a[3333] = 10000 + 4;a[1222] = 10000 + 5;a[459] = 10000 + 6;a[9999] = 10000 + 7;a[8778] = 10000 + 8;a[5897] = 10000 + 9;a[44] = 10000 + 10;PrintTopK(a, n, 10);}
打印的结果都是大于10000的说明我们的思路成立。