排版丑陋，不要见怪

传送门

文章目录

• A. Lines
• • 题面
  • 输入
  • 输出
  • 样例
  • 思路
  • 代码
• D. Swap Permutation
• • 题面
  • 输入
  • 输出
  • 样例
  • 思路
  • 代码
• E. Black Jack
• • 签到
• F. This is a number theory problem
• • 签到
• H.Spring tree
• • 题面
  • 输入
  • 输出
  • 样例
  • 思路
  • 代码
• K. Target（待补：扫描线）

A. Lines

题面

输入

输出

样例

输入#1

2
3 1
1 0
2 0
3 0
1 1
-1 2

输出#1

Bob
Alice

思路

题意：$n$ 条直线，Alice 和 Bob 依次画 $k$ 条直线。最终会有 $n+2k$ 条，奇数交点 Bob 赢，否则 Alice 赢。

首先按 斜率 进行分组，记 $cnt(k)$ 表示斜率为 $k$ 的直线条数。

考虑 Bob 最后一步操作：如果存在某个斜率 k ′ {k'} k′ ，有 c n t ( k ′ ) {cnt(k')} cnt(k′) 为奇数，那么 Bob 是必胜的。

Bob 画一条斜率为 k ′ {k'} k′ 的直线后

• 如果是奇数，Bob 赢
• 如果是偶数，那么这条直线就换成一个没出现过的斜率，会相对 增加 c n t (k′ ) {cnt(k')} cnt(k′) 个交点，仍然保证最后为奇数， Bob 赢

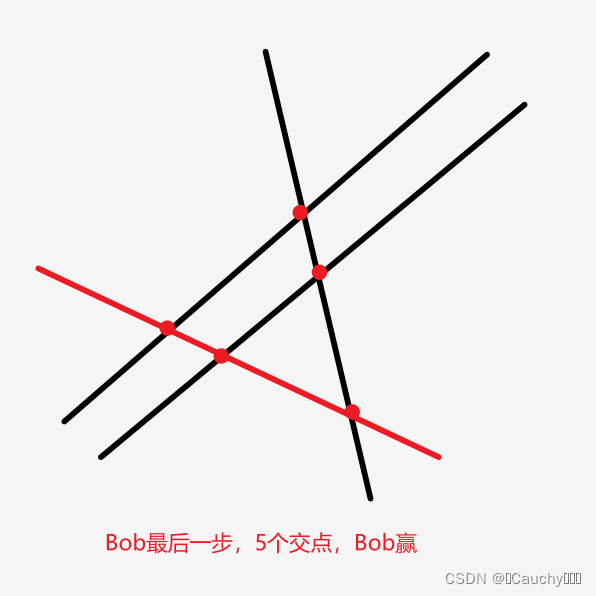
• 所以 Alice 一定要留给 Bob 所有的 $cnt(k)$ 都为偶数的局面。

  • 那么每次轮到 Alice 操作，必须 恰有 一个 $cnt(k)$ 为奇数

• Alice 每次只能将一个大小为奇数的 $cnt$ 转为偶数

• Bob 每次都能增加一个大小为奇数的组（可选择画未出现过的斜率）

那么也就是在局面开始之前，必须恰有一个大小为奇数的组，Alice 才能赢。

否则 Bob 赢。

代码

map<int, int> mp;void solve() {    mp.clear();    int n, k; cin >> n >> k;    rep(i, 0, n) { int a, b; cin >> a >> b; mp[a] ++;    }    int res = 0;    for (auto &it: mp) { if(it.se & 1) res++;    }    if(res == 1) cout << "Alice" << endl;    else cout << "Bob" << endl;}

D. Swap Permutation

题面

输入

输出

样例

输入#1

4 2
1 2 3 4

输出#1

2

输入#2

5 1
2 1 4 3 5

输出#2

2

思路

依题意：$i$ 连向 p i {p_i} pi​ ，可对数组 $p$ 进行 $k$ 次交换操作，计算最少连通块数量。

由于 p i {p_i} pi​ 数组是 $1$ ~ $n$ 的全排列，不难发现有一个性质： 一旦形成一个连通块，那么

• 要么是独立一个自环
• 要么必定是一个环

那么还能发现，在一个环（连通块）中节点的 p i {p_i} pi​ 和 p j {p_j} pj​ 交换必定有一者会回到自己位置（即独立成环）

到此，我们可知与原先数组的连通性有关，我们可以先计算出原连通块数：$cnt$。

那么交换 $k$ 次可分为以下两种情况：

• $k>=cnt-1$

  • 那么花费 $cnt-1$ 次，我们就可以将连通块数变为 $1$

  • 剩下 $k-cnt+1$ 次：

    • 奇数：等价于全连通块中交换 $1$ 次，会多出 $1$ 个独立块
    • 偶数：等价于交换 $0$ 次，连通块数不变

• $k<cnt-1$

  • 连通块数变为 $cnt-k$

代码

• 连通块直接用 并查集+set，s.insert(fa[find(i)])，切记别写错，fa[find(i)]。（别问我为什么

#include using namespace std;const int N = 200010;int fa[N];int find(int x) {    return fa[x] = fa[x] == x ? x : find(fa[x]);}int main() {    int n, k; cin >> n >> k;    for (int i = 1; i <= n; i++) fa[i] = i;    for (int i = 1; i <= n; i++) { int x; cin >> x; fa[find(x)] = find(i);    }    int cnt = 0;    set<int> s; for (int i = 1;i <= n;i++) s.insert(fa[find(i)]);    cnt = s.size();    if(k >= cnt - 1) { cout << ((k - cnt + 1) % 2) + 1 << endl;    } else { cout << cnt - k << endl;    }    return 0;}

E. Black Jack

签到

#include using namespace std;int main() {    int n; cin >> n;    int sum = 0, cnt = 0;    for (int i = 0; i < n; i++) { int x; cin >> x; if(sum + x > 21) break; else sum += x, cnt += 1;    }    cout << cnt << endl;    return 0;}

F. This is a number theory problem

签到

#include using namespace std;bool check(int x) {    int res = 0;    while(x) { res += x % 10; x /= 10;    }    if(res == 1) return false; // hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh    for (int i = 2; i <= res / i; i++) { if(res % i == 0) return false;    }    return true;}int main() {    int n; cin >> n;    for (int i = 2; i <= 10000000; i++) { if(check(i)) n -= 1; if(n == 0) {     cout << i << endl;     return 0; }    }    return 0;}

H.Spring tree

题面

输入

输出

样例

输入#1

4
1 2 3 4
1 2
2 3
3 4

输出#1

23

Note

In the test case, keep original arrangement is a good idea.
maximum depth = (1+4) + (1+4+3) + (1+4+3+2) = 23

思路

首先我们发现，更重的球会更倾向于放到深度最深的位置。

枚举最优解中深度最深的叶子 $leaf$，那么最优解会怎样放置呢？

首先最重的球一定给 $leaf$，然后考虑 $leaf$ 的父亲 $parent(leaf)$，那么最重的 $size(parent(leaf))$个球一定都在 parent(leaf) 的子树中（其中 $size(u)$ 表示 $u$ 的子树大小）… 依次类推。

那么我们可以把节点 $u$ 的权值设成 $w(size(u))$ 接着求出树上从根到树叶找出一条权值和最大的路径即可，这个可以用 $O(n)$ 的 $DP$ 来实现，需要注意的是根节点没有连向父亲的弹簧，所以根节点权值应该设成 $0$.

详见注释

代码

#includeusing namespace std;#define int long longconst int N = 250010, M = N << 1;int n, ans;int dp[N], sz[N], w[N], s[N];vector<int> e[N];void dfs(int u, int f) {    sz[u] = 1;    for (auto &x: e[u]) { if(x == f) continue; dfs(x, u); sz[u] += sz[x]; // 经典处理size数组 dp[u] = max(dp[x], dp[u]);  // 对于当前u为根节点，我们要维护孩子中的最长链    }    dp[u] += s[sz[u]] + 1; // 累加上u节点上面弹簧的权值   // 该权值：u下子树所有值，从大到小赋值，也就是我们处理好的前缀和    if(u != 1) ans = max(ans, dp[u]); // 根节点上面无弹簧啦}void solve() {    cin >> n;    for (int i = 1; i <= n; i++) cin >> w[i];    // 建无向图    for (int i = 1; i < n; i++) { int u, v; cin >> u >> v; e[u].push_back(v); e[v].push_back(u);    }    // 由于弹簧的性质，我们从叶子向上一定是个累加的过程。    // 这里从大到小排序，并且预处理好前缀和    sort(w + 1, w + n + 1, [=](int A, int B){ return A > B; });    for (int i = 1; i <= n; i++) s[i] = s[i - 1] + w[i];    dfs(1, 0);    cout << ans << endl;}signed main() {int _ = 1;while(_--) { solve(); }return 0;}

K. Target（待补：扫描线）