网站导航
> 文档中心 > 数据结构与算法_01_谨慎使用的递归算法

数据结构与算法_01_谨慎使用的递归算法

网友: 文档中心 2022-06-12 16:23:21

数据结构与算法，系列文章传送地址，请点击本链接。

目录

一、如何理解递归

二、递归需要满足三个条件

三、如何写递归代码

四、代码模板

五、常见错误和注意事项

1、递归代码要警惕堆栈溢出

2、递归代码要警惕重复计算

六、递归写法改成非递归

七、案例

一、如何理解递归

递归本身并不好理解，举一个生活中的栗子来理解一下。

周末你带着女朋友去电影院看电影，女朋友问你，咱们现在坐在第几排啊？电影院里面太黑了，看不清，没法数，现在你怎么办？

于是你就问前面一排的人他是第几排，你想只要在他的数字上加一，就知道自己在哪一排了。但是，前面的人也看不清啊，所以他也问他前面的人。就这样一排一排往前问，直到问到第一排的人，说我在第一排，然后再这样一排一排再把数字传回来。直到你前面的人告诉你他在哪一排，于是你就知道答案了。

一个非常标准的递归求解问题的分解过程，去的过程叫“递”，回来的过程叫“归”。基本上，所有的递归问题都可以用递推公式来表示。刚刚这个生活中的例子，我们用递推公式将它表示出来就是这样的：

f(n)=f(n-1)+1 其中，f(1)=1

f(n) 表示你想知道自己在哪一排，f(n-1) 表示前面一排所在的排数，f(1)=1 表示第一排的人知道自己在第一排。有了这个递推公式，我们就可以很轻松地将它改为递归代码，如下：

int f(int n) {

  if (n == 1) return 1;

  return f(n-1) + 1;

}

二、递归需要满足三个条件

1. 一个问题的解可以分解为几个子问题的解

何为子问题？子问题就是数据规模更小的问题。比如，前面讲的电影院的例子，你要知道，“自己在哪一排”的问题，可以分解为“前一排的人在哪一排”这样一个子问题。

2. 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样

比如电影院那个例子，你求解“自己在哪一排”的思路，和前面一排人求解“自己在哪一排”的思路，是一模一样的。

3. 存在递归终止条件

把问题分解为子问题，把子问题再分解为子子问题，一层一层分解下去，不能存在无限循环，这就需要有终止条件。还是电影院的例子，第一排的人不需要再继续询问任何人，就知道自己在哪一排，也就是 f(1)=1，这就是递归的终止条件。

三、如何写递归代码

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

四、代码模板

Java
public void recur(int  level,int param) {
    //终止条件
    if(level > MAX_LEVEL){
        return;
    }
   
    //处理过程
    process(level,param);
   
    //下钻
    recur(level + 1，newParam);
   
    //存储当前状态（按需书写）
   
}

五、常见错误和注意事项

1、递归代码要警惕堆栈溢出

在实际的软件开发中，编写递归代码时，我们会遇到很多问题，比如堆栈溢出。而堆栈溢出会造成系统性崩溃，后果会非常严重。为什么递归代码容易造成堆栈溢出呢？我们又该如何预防堆栈溢出呢？

我在“栈”那一节讲过，函数调用会使用栈来保存临时变量。每调用一个函数，都会将临时变量封装为栈帧压入内存栈，等函数执行完成返回时，才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

因此建议如果深度太深可以考虑其他方法处理。

2、递归代码要警惕重复计算

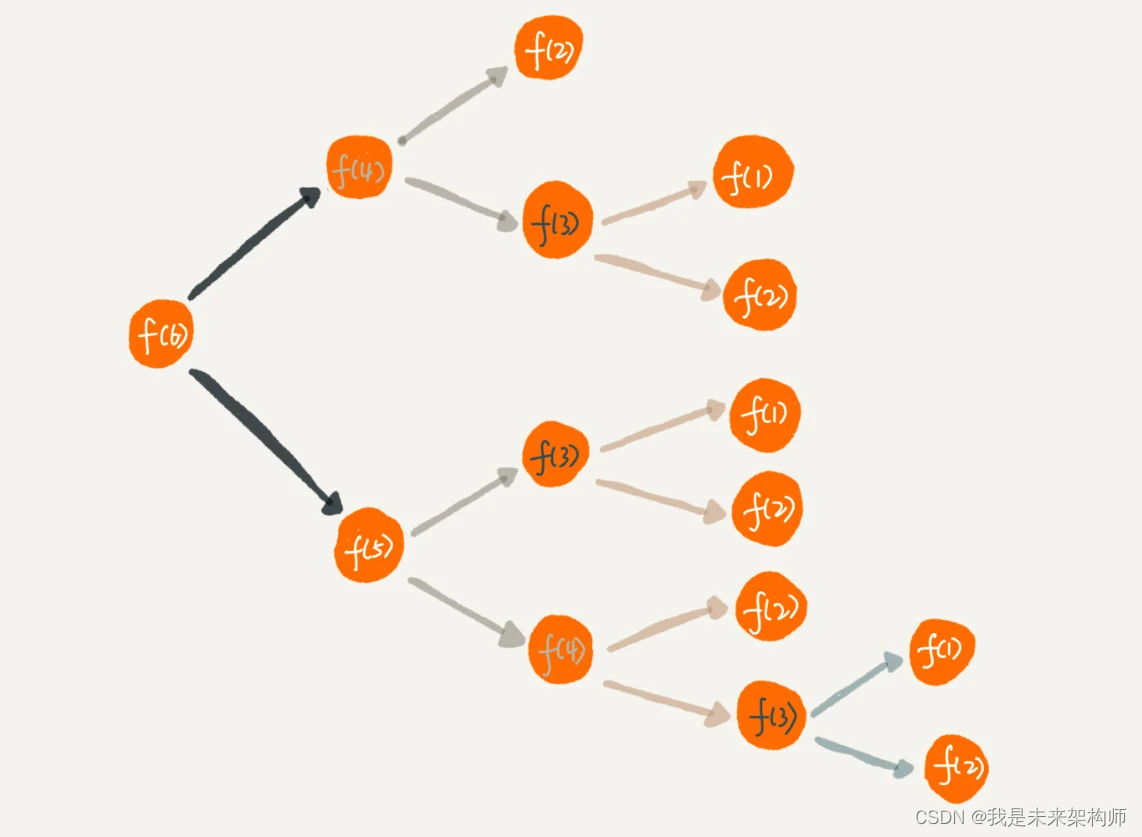
如下一个计算分解图，我们发现大量的f(4),f(3)....的重复计算，用什么方案解决呢？

为了避免重复计算，我们可以通过一个数据结构（比如散列表）来保存已经求解过的 f(k)。当递归调用到 f(k) 时，先看下是否已经求解过了。如果是，则直接从散列表中取值返回，不需要重复计算，这样就能避免刚讲的问题了。

六、递归写法改成非递归

递归有利有弊，利是递归代码的表达力很强，写起来非常简洁；而弊就是空间复杂度高、有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多等问题。所以，在开发过程中，我们要根据实际情况来选择是否需要用递归的方式来实现。

我们一般可以通过迭代法来改变递归的写法。

Java
//递归法
int f(int n) {
  if (n == 1) return 1;
  return f(n-1) + 1;
}

//迭代法
int f(int n) {
  int ret = 1;
  for (int i = 2; i <= n; ++i) {
    ret = ret + 1;
  }
  return ret;
}

那是不是所有的递归代码都可以改为这种迭代循环的非递归写法呢？

笼统地讲，是的。因为递归本身就是借助栈来实现的，只不过我们使用的栈是系统或者虚拟机本身提供的，我们没有感知罢了。如果我们自己在内存堆上实现栈，手动模拟入栈、出栈过程，这样任何递归代码都可以改写成看上去不是递归代码的样子。

但是这种思路实际上是将递归改为了“手动”递归，本质并没有变，而且也并没有解决前面讲到的某些问题，徒增了实现的复杂度。

七、案例

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

Java
class Solution {
    public int climbStairs(int n) {
        int  q = 0;
        int  p = 0;
        int res = 1;
        for(int i = 1;i<=n;i++) {
            p = q;
            q = res;
            res = p + q;
        }
        return res;
    } 
}

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

输入：n = 3

输出：["((()))","(()())","(())()","()(())","()()()"]

输入：n = 1

输出：["()"]

TypeScript
class Solution {
    private ArrayList res;
    public List generateParenthesis(int n) {
        res = new ArrayList();
        generate(n,0,0,"");
        return res;

    }
    public void generate(int n,int left,int right,String str){

        if (left == n && right == n){
            res.add(str);
        }
        if (left < n) {
            generate(n,left+1,right,str+"(");
        }
        if (left > right) {
           generate(n,left,right+1,str+")");
        }
    }
}

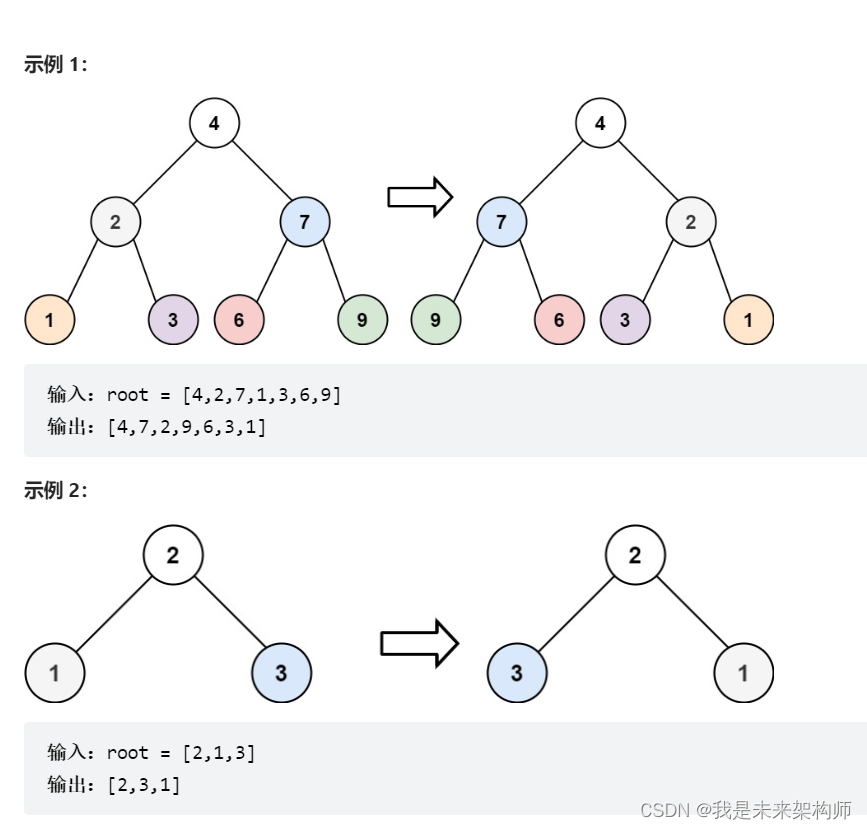
226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

Java
class Solution {
    public TreeNode invertTree(TreeNode root) {
         if(root == null) {
            return  null;
        }
        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);
        root.left = right;
        root.right =left;
        return root;
    }
}

98. 验证二叉搜索树

完成这道题，共有三种方法：递归，迭代，中序遍历

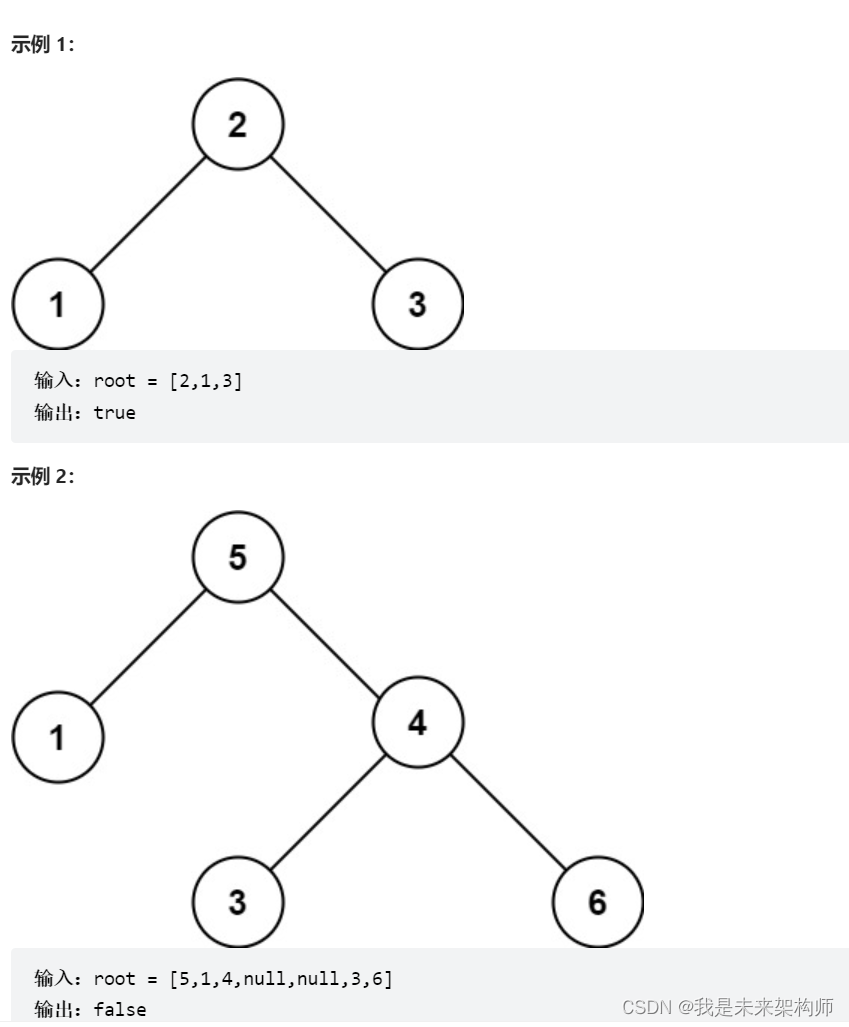
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。

节点的右子树只包含 大于 当前节点的数。

所有左子树和右子树自身必须也是二叉搜索树。

声明：文章内容是极客时间专栏学习的学习笔记，会做简化或调整，欢迎大家留言和评论。

数据结构与算法，系列文章传送地址，请点击本链接。https://blog.csdn.net/wanghaiping1993/article/details/125092448

网络标签：

相关问题