可持久化全解
可持久化全解
- 算法思想
-
- 权值线段树
- 可持久化权值线段树(主席树)
- 可持久化数组
-
- rope
- 可持久化并查集
-
- 带删并查集
- 可持久化Trie
- 可持久化平衡树
-
- fhq Treap
-
- 分裂
- 合并
- 区间操作
- 其他操作
- 平衡树的可持久化
- 训练
-
- LuoguP3369
- LuoguP3919
- LuoguP4567
- LuoguP3402
- 2019南昌A
- POJ2104
- LuoguP4735
- HDU4348(题目已无法提交)
- SP10628
- UVA12538
- UVA11987
- LuoguP4359
- LuoguP3391
- LuoguP3835
- LuoguP5055
- LuoguP4592
- 总结
- 参考文献
算法思想
可持久化是一个很大的部分,一般来说,具有可持久化性质的数据结构都具有这样的特征:存储了对应数据结构所有的历史版本,并通过数据重复使用减少复杂度,基本做法是在每次操作之后仅对已修改的部分创建副本用于保存,其余未修改部分重用,许多数据结构都可以写成可持久化形式,线段树,Trie,并查集,甚至数组
本篇只介绍一些常用的可持久化数据结构,例如主席树,可持久化并查集,可持久化trie,fhq Treap等,不介绍可持久化树状数组,可持久化左偏树这一类不常用的数据结构
权值线段树
权值线段树是主席树与可持久化数组实现的基石,对于一般的线段树来说,其节点多用于存储以区间为单位的相关值,如和、最值等,而权值线段树,其节点则用于存储以取值范围为单位的相关值,即对于一个序列来说,在某一特定值域内的元素个数,节点范围为值域,权值线段树可以查询全局的k小值,某个值在全局的排名以及前驱与后继(和Treap有些类似),但是当值域过大时需要离散化,但其实如果只是实现这些的话,其实不如用平衡树,因为不用离散化,码量大一些而已
权值线段树举例如下,插入序列{1,4,2,3}
一开始各节点值为0,权值线段树节点存储的是值域内对应值的出现次数
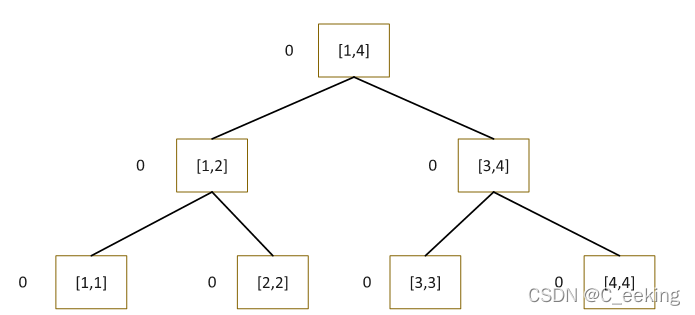 插入1之后,对应的三个节点被赋值
插入1之后,对应的三个节点被赋值
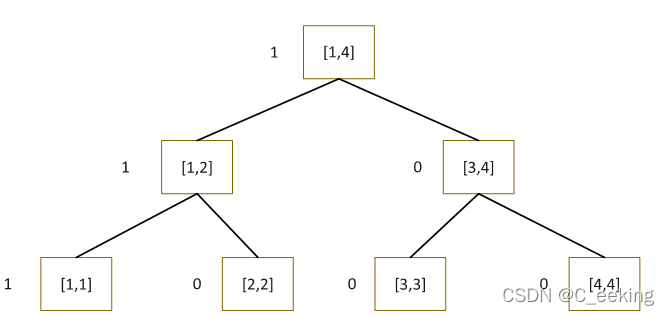 插入2之后,对应的节点给更新,3,4同理
插入2之后,对应的节点给更新,3,4同理
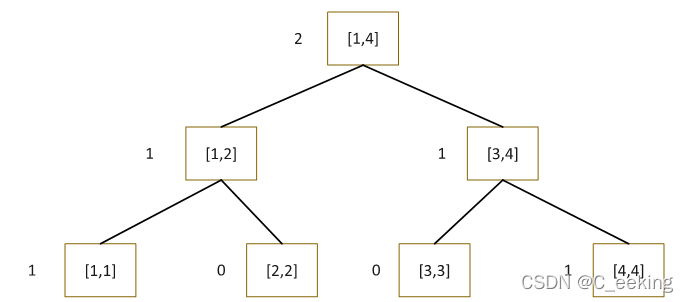 最后的结果如下
最后的结果如下
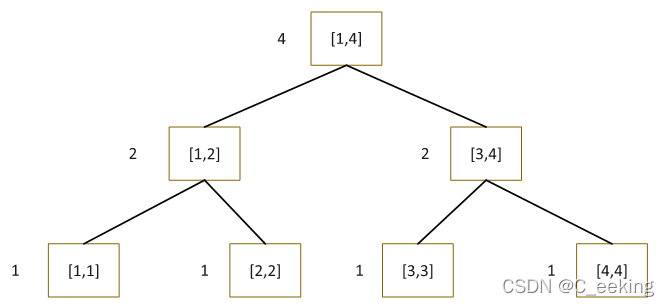 由于权值线段树的形状都相同,只是节点的权值不同,所以这样的两棵线段树是可以相减的(相减定义为对应节点的权值相减)
由于权值线段树的形状都相同,只是节点的权值不同,所以这样的两棵线段树是可以相减的(相减定义为对应节点的权值相减)
代码
//pos为单点修改的位置,v为要修改的值void Update(int pos,int v,int l,int r,int rt) { if(l==r) { seg[rt].sum+=v; return ; } int mid=(l+r)/2; if(pos<=mid)Update(pos,v,l,mid,rt<<1); else Update(pos,v,mid+1,r,rt<<1|1); seg[rt].sum=seg[rt<<1].sum+seg[rt<<1|1].sum;}//在[l,r]范围找最值int FindMax(int rt,int l,int r) {//找到当前区间最大值 if(l==r)return l; int mid=(l+r)/2; if(seg[rt<<1|1].sum)return FindMax(rt<<1|1,mid+1,r);//右区间存在 return FindMax(rt<<1,l,mid);}int FindMin(int rt,int l,int r) {//找到区间最小值 if(l==r)return l; int mid=(l+r)/2; if(seg[rt<<1].sum)return FindMin(rt<<1,l,mid);//左区间存在 return FindMin(rt<<1|1,mid+1,r);}int Pre(int v,int rt,int l,int r) {//前驱 if(r<v) {//如果查找值比区间右端点大,代表前驱可能在右区间 if(seg[rt].sum)return FindMax(rt,l,r); return 0; } int mid=(l+r)/2,res;//到这里说明v在[l,r]中 if(mid<v-1&&seg[rt<<1|1].sum&&(res=Pre(v,rt<<1|1,mid+1,r))) return res;//如果比v小的值在右区间,它可能是前驱 return Pre(v,rt<<1,l,mid);//在左区间}int After(int v,int rt,int l,int r) {//后继 if(v<l) { if(seg[rt].sum)return FindMin(rt,l,r); return 0; } int mid=(l+r)/2,res; if(v<mid&&seg[rt<<1].sum&&(res=After(v,rt<<1,l,mid))) return res; return After(v,rt<<1|1,mid+1,r);}//值查排名int QueryValue(int v,int rt,int l,int r) {//按照值查找 if(r<v)return seg[rt].sum;//v比r大,代表r之前的都比v小 int mid=(l+r)/2,res=0;//到这里就v比r小 res+=QueryValue(v,rt<<1,l,mid);//先在左区间统计 if(mid<v-1)res+=QueryValue(v,rt<<1|1,mid+1,r);//如果v超过了左区间 return res;}//排名查值int QueryRank(int k,int rt,int l,int r) {//按照排名查找 if(l==r)return l; int mid=(l+r)/2; if(seg[rt<<1].sum>=k)return QueryRank(k,rt<<1,l,mid); else return QueryRank(k-seg[rt<<1].sum,rt<<1|1,mid+1,r);}//离散化 for(int i=1; i<=n; i++) {//离线处理 cin >>opt[i]>>q[i].v; q[i].id=i; } sort(q+1,q+1+n);//排序方便离散化 dic[a[q[1].id]=++cnt]=q[1].v; /*q为记录的询问,q[1].id为数值最小的询问对应的编号 a[q[1].id]为询问被离散化成cnt,dic[cnt]为记录询问对应的真实值 */ for(int i=2; i<=n; i++) { if(q[i].v!=q[i-1].v)cnt++; dic[a[q[i].id]=cnt]=q[i].v; }//也可以采用二分sort(b+1,b+1+n);int tot=unique(b+1,b+1+n)-b-1;//去重int pos=lower_bound(b+1,b+1+tot,a[i])-b;//a[i]的位置可持久化权值线段树(主席树)
介绍可持久化线段树之前,首先探寻一下权值线段树的一点拓展
仍然是权值线段树,插入了{1,4,2,3}
将插入3之后的线段树减去插入1之后的线段树,得到如图所示,减去之后可以得到序列第2个元素到第3个元素的权值线段树,即一个区间和,这是前缀和的思想,对于任意一个区间 [ l , r ] [l,r] [l,r]的权值线段树都可以用区间为 [ 1 , r ] , [ 1 , l − 1 ] [1,r],[1,l-1] [1,r],[1,l−1]的两棵权值线段树相减得到,那么就可以快速查询区间问题
 显然,如果每插入一个元素就创建一个权值线段树,那么空间开销必然会很大,有很多重复的节点,可持久化线段树就对这一点进行了优化:在创建权值线段树过程中仅对权值变化的节点进行插入,重用未修改的节点
显然,如果每插入一个元素就创建一个权值线段树,那么空间开销必然会很大,有很多重复的节点,可持久化线段树就对这一点进行了优化:在创建权值线段树过程中仅对权值变化的节点进行插入,重用未修改的节点
举例如下
插入1之后,对修改的节点进行重建,然后复用未修改节点
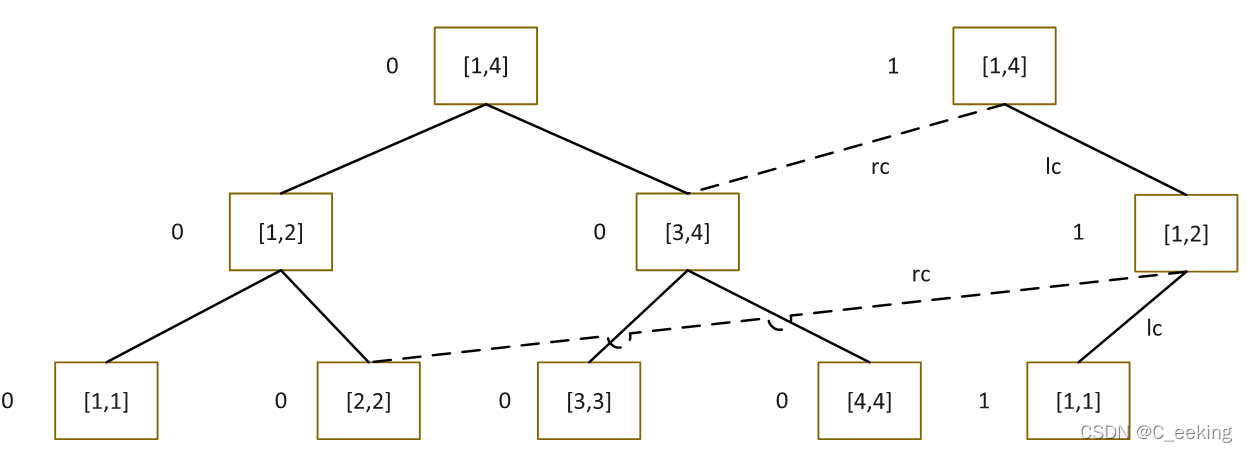
插入2之后
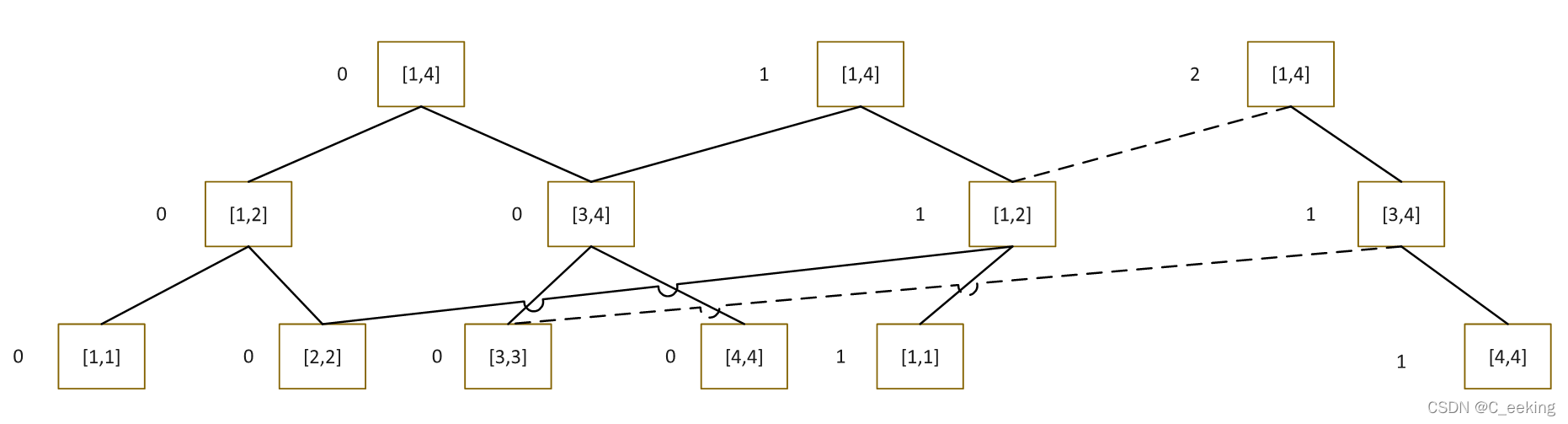
可持久化的基本使用都基于权值线段树,但是由于是多棵线段树并且存在节点复用的情况,所以构造上与普通的线段树还是有区别的
代码
#define lc seg[i].ch[0]#define rc seg[i].ch[1]#define Lc seg[j].ch[0]#define Rc seg[j].ch[1]struct node { int num,ch[2]; //这里必须用,因为每个节点的左右子树并不是单个线段树那样简单} seg[maxn*20];void update(int &i,int j,int l,int r,int v) { i=++cnt;//创建新的节点存储区间信息 seg[i]=seg[j];//初始化为上一版本 seg[i].num++;//在这一版本上进行修改 if(l==r)return; int mid=(l+r)>>1; if(v<=mid)update(lc,Lc,l,mid,v); //权值线段树,v即对应的下标增加 else update(rc,Rc,mid+1,r,v);}int query(int i,int j,int l,int r,int v) { if(l==r)return l; int s=seg[Lc].num-seg[lc].num;//计算版本之间的差值 int mid=(l+r)>>1; if(v<=s)return query(lc,Lc,l,mid,v); //类似平衡树,如果区间内的个数比v大,则v必然在区间内 else return query(rc,Rc,mid+1,r,v-s); //否则在区间外}//排名查值int QuerySum(int i,int j,int l,int r,int L,int R) { if(l>=L&&r<=R)return seg[i].val-seg[j].val; int mid=(l+r)>>1,res=0; if(L<=mid)res+=QuerySum(lc,Lc,l,mid,L,R);//必须逐个判断这样写 if(R>mid)res+=QuerySum(rc,Rc,mid+1,r,L,R); return res;}//区间和可持久化数组
可持久化数组一般来说,指的是对一个数组进行操作,需要保存各次操作的版本信息,并且支持单点修改和单点查询(基于版本),简单来说,如果没有版本的限制的话,就是对数组下标直接进行修改,加上版本之后,就需要维护版本了,由于不可能用简单的线段树维护,而主席树正好可以维护版本,那么主席树就用来保存当前版本这一下标的值即可
代码
void Build(int &i,int l,int r) {//建树 i=++cnt; if(l==r) { scanf("%d",&seg[i].val); return ; } int mid=(l+r)>>1; Build(lc,l,mid); Build(rc,mid+1,r);}void Update(int &i,int j,int l,int r,int pos,int v) {//更新 i=++cnt; if(l==r) { seg[cnt].val=v; return ; } lc=Lc,rc=Rc;//先复制 int mid=(l+r)>>1; if(pos<=mid)Update(lc,Lc,l,mid,pos,v); else Update(rc,Rc,mid+1,r,pos,v);}int Query(int i,int l,int r,int pos) {//查询,i为版本的根节点 if(l==r) return seg[i].val; int mid=(l+r)>>1; if(pos<=mid) return Query(lc,l,mid,pos); return Query(rc,mid+1,r,pos);}rope
rope为STL自带的一种可持久化数组实现,底层实现采用块状链表,运用了分块的思想,所以时间复杂度是 O ( n ) O(\sqrt{n}) O(n),,但是它可以实现 O ( 1 ) O(1) O(1)复制,与其他的STL的缺点一样,有较大的常数,基本用法和支持的都和string一样,引用和头文件代码如下
#include using namespace __gnu_cxx;rope<char>r;一般的substr,erase,at,insert,replace等函数都可以使用,但最重要的还是拷贝,代码如下
rope<char>*a,*b;a=new rope<char>;b=new rope<char>(*a)rope和莫队的效率有的一比,但是所能适应的数据范围其实很小,一般来说,由于 O ( n n ) O(n\sqrt{n}) O(nn)的复杂度, n n n的极限取值不超过 1 0 5 10^5 105
可持久化并查集
可持久化并查集是基于可持久化数组来实现的,在并查集中,最重要的是记录节点之间的父子关系的,由于并查集的父数组是用可持久化数组来维护的,那么对并查集的优化就不能用路径压缩了,因为对于可持久化数组来说,每有一次单点修改,可持久化数组就会多一个版本,所以不能用路径压缩来优化,这里采用按秩合并的优化方式,即按照深度来合并,高度小合并到高度大的子树上,由于涉及到子树高度,那么可持久化数组就还需要维护不同版本树的高度
由于需要维护两个可持久化数组,那么就需要用两个主席树,使用的内存池开始一起的,一般来说,需要开几个主席树,就需要开多少个存储根的数组,如果数量过多,可以将根数组开成二维的
代码
struct node { int val,ch[2];} seg[maxn*60];void Build(int&i,int l,int r) {//建树,这里的树是记录父节点树 i=++cnt; if(l==r) { seg[i].val=l; return ; } int mid=(l+r)>>1; Build(lc,l,mid); Build(rc,mid+1,r);}void Update(int&i,int j,int l,int r,int pos,int v) {//这里的树既可以是深度树也可以是父节点树 i=++cnt; seg[i]=seg[j]; if(l==r) { seg[i].val=v; return ; } int mid=(l+r)>>1; if(pos<=mid)Update(lc,Lc,l,mid,pos,v); else Update(rc,Rc,mid+1,r,pos,v);}int Query(int i,int l,int r,int pos) { if(l==r)return seg[i].val; int mid=(l+r)>>1; if(pos<=mid)return Query(lc,l,mid,pos); return Query(rc,mid+1,r,pos);}int Find(int i,int x) { int fx=Query(rtfa[i],1,n,x); return fx==x?x:Find(i,fx);//无路径压缩}void Merge(int i,int x,int y) { x=Find(i-1,x);//找上一版本的祖宗,因为要构造这一版本,当前版本为空 y=Find(i-1,y);//同理 if(x==y) {//属于同一集合,直接复制上版本的所有情况 rtfa[i]=rtfa[i-1]; rtdeep[i]=rtdeep[i-1]; } else {//按秩合并 int dx=Query(rtdeep[i-1],1,n,x);//获得深度 int dy=Query(rtdeep[i-1],1,n,y);//同上 if(dx<dy) { Update(rtfa[i],rtfa[i-1],1,n,x,y);//将i版本x的父节点更新为y rtdeep[i]=rtdeep[i-1];//复制节点 } else if(dx>dy) { Update(rtfa[i],rtfa[i-1],1,n,y,x);//将i版本y的父节点更新为x rtdeep[i]=rtdeep[i-1];//复制节点 } else { Update(rtfa[i],rtfa[i-1],1,n,x,y);//将i版本x的父节点更新为y Update(rtdeep[i],rtdeep[i-1],1,n,y,dy+1);//深度增加 } }}带删并查集
带删并查集指的是从一个集合中扣去一个点,将这个点作为单独的集合分离或者将这个点与其他集合合并
最朴素的想法是暴搜找到这个点的父节点和所有子节点,然后直接切断联系,然后将分离出来的点进行合并,这样的花销过大
在并查集中,有一种常用的技巧,即设置虚点(也可以是相反点),例如,如果a和b必定不在一个集合内,那么就可以合并a+n和b,用于代表这个条件,而a+n就是虚点
那么,如果对每个点都设置一个虚点,例如对节点 i i i,其虚点编号就是 i + n i+n i+n,这两点就必然位于同一集合,那么对集合的合并操作就可以转换成对虚节点的操作,为什么要这样做呢?因为只对虚节点操作的话,能够保证所有的非虚点必为叶子节点,那么如果要进行拆点合并的话,那么直接对叶子节点操作即可,也就直接更改叶子节点的父节点,这样的话开销就小了
可持久化Trie
可持久化Trie具有其他可持久化数据结构的特点,存储所有的历史版本,并复用可利用信息,每次只会对变化的节点修改或者新建,可持久化Trie的节点与普通Trie节点相同,可以用数组来存储节点编号
假设当前可持久化Trie的树根为root[i-1],设p=root[i-1]现在要拆入一个字符s[j],算法步骤如下
- 创建一个新节点q,令当前树根root[i]=q
- 若root[i-1]不为空,则将root[i-1]相关信息全部复制给q对应节点,对于每个字符x,trie[root[i]][x]=trie[root[i-1]][x]
- 创建一个新节点y,此时进行插入操作,trie[root[i-1]s[j]]=y,此时的q节点除了s[j]与root[i-1]不同,其他都相同
- 递归进行,令p=trie[p][s[j]],q=trie[q][s[j]],j=j+1
下面给出代码(以统计区间最大异或和为例)
代码
void Insert(int id,int k,int q,int p) { maxs[q]=id;//记录这个点是第几个数的 if(k<0)return ; int c=s[id]>>k&1; if(p)trie[q][c^1]=trie[p][c^1];//如果有值,需要复制 trie[q][c]=++cnt;//必须先复制后赋值,因为可能赋值值被更新 Insert(id,k-1,trie[q][c],trie[p][c]);}int Query(int q,int k,int val,int l) { if(k<0)return s[maxs[q]]^val; int c=val>>k&1; if(maxs[trie[q][c^1]]>=l)return Query(trie[q][c^1],k-1,val,l); //下标不小于l-1 return Query(trie[q][c],k-1,val,l);}可持久化平衡树
fhq Treap
顾名思义,fhq Treap的基础是Treap,所以需要先掌握Treap才能理解fhq Treap的思想,Treap详情可以参考Treap笔记
fhq Treap与Treap相同,同样是利用随机数当索引,然后用堆来维护整棵树的结构,不过与Treap不同的是,fhq Treap的所有操作都是通过分裂和合并来完成的,对于每个节点来说,需要保存左右子树的编号,当前节点的值,索引以及子树大小
分裂
分裂有两种,按值分裂和按照子树大小分裂
按值分裂:树被拆成两棵树,一棵树满足其所有节点都小于等于给定值,另一棵满足所有节点都大于给定值
按大小分裂,把树拆成两棵树,一棵树大小等于给定大小,其余的在另一棵里
代码
void SplitByValue(int now,int val,int &x,int &y) { if(!now)x=y=0; else { if(fhq[now].val<=val)//如果值小于给定值,now的左边必然都要分出来,更改now的右边 x=now,SplitByValue(fhq[now].rc,val,fhq[now].rc,y); else y=now,SplitByValue(fhq[now].lc,val,x,fhq[now].lc); Update(now); }}void SplitBySize(int now,int large,int &x,int &y) { if(!now)x=y=0; else { if(fhq[fhq[now].lc].num<large) {//左子树的大小比值小 x=now; SplitBySize(fhq[now].rc,large-fhq[fhq[now].lc].num-1,fhq[now].rc,y);//在右子树上切剩下的部分 } else { y=now; SplitBySize(fhq[now].lc,large,x,fhq[now].lc);//同理 } Update(now); }}合并
合并即把两棵树合并成一棵树,其中x树上的所有值都小于等于y树上的所有制,新树仍然满足条件
代码
int Merge(int x,int y) { if(!x||!y)return x+y; if(fhq[x].pri>fhq[y].pri) {//按照大根堆的思路合并 fhq[x].rc=Merge(fhq[x].rc,y); Update(x); return x; } fhq[y].lc=Merge(x,fhq[y].lc); Update(y); return y;}区间操作
假设要操作的区间为 [ l , r ] [l,r] [l,r],那么直接在树中把这一段拆出来,然后对这一段进行完操作之后合并回去,,具体步骤为把fhq Treap按照大小l-1拆成x和y,之后再把y按照r-l+1拆分成y和z,对y进行操作,最后合并xyz
以上只是将区间拆了出来,但是对区间的操作肯定也不能直接逐个操作,这样的话处理就没有了意义,通过前面的更新,插入可以看到,fhq Treap的维护过程非常类似于线段树,因此,可以用懒标记来维护,例如,如果想要对一个区间进行翻转,对这个区间维护懒标记,如果没有,就打上,如果有,就去掉,因为两次翻转等于没转,向下递推的思路和线段树一样
以翻转为例
代码
void PushDown(int now) {//向下更新 swap(fhq[now].lc,fhq[now].rc);//先翻转区间 fhq[fhq[now].lc].mark^=1;//打标记 fhq[fhq[now].rc].mark^=1; fhq[now].mark=0;}int Merge(int x,int y) { if(!x||!y)return x+y; if(fhq[x].pri>fhq[y].pri) { if(fhq[x].mark)PushDown(x); fhq[x].rc=Merge(fhq[x].rc,y); Update(x); return x; } if(fhq[y].mark)PushDown(y); fhq[y].lc=Merge(x,fhq[y].lc); Update(y); return y;}void Reverse(int l,int r) { int x,y,z; SplitBySize(root,l-1,x,y); SplitBySize(y,r-l+1,y,z); fhq[y].mark^=1; root=Merge(Merge(x,y),z);}其他操作
插入
以插入的值为界限,将树分裂成x和y,合并x和新节点,然后合并y
代码
inline int New(int v) {//新节点 fhq[++cnt].val=v; fhq[cnt].lc=fhq[cnt].rc=0; fhq[cnt].num=1;//子树大小 fhq[cnt].pri=rand(); return cnt;}void Insert(int val) { int x,y; SplitByValue(root,val,x,y); root=Merge(Merge(x,New(val)),y);}删除
以要删除的值为界限将树分裂成a和b,再按值-1将a分裂成x和y,那么此时y上的所有值都是等于删除值的,删除y的一个点即可,让y等于合并y的左子树和右子树的的结果,等效于删了根节点
代码
void Delete(int val) { int x,y,z; SplitByValue(root,val,x,z); SplitByValue(x,val-1,x,y); y=Merge(fhq[y].lc,fhq[y].rc); root=Merge(Merge(x,y),z);}排名查值/值查排名
和Treap基本类似,利用二叉搜索树性质即可
代码
int GetByRank(int k) { int now=root; while(now) { if(fhq[fhq[now].lc].num+1==k) return fhq[now].val; if(fhq[fhq[now].lc].num>=k) now=fhq[now].lc; else { k-=fhq[fhq[now].lc].num+1; now=fhq[now].rc; } } return -1;}int GetByValue(int val) { int x,y,res; SplitByValue(root,val-1,x,y); res=fhq[x].num+1; root=Merge(x,y); return res;}前驱/后继
前驱:按照给定值-1将树分裂成x和y,则x的右下角树为前驱
后继:按照给定值分裂成x和y,则y的左下角为后继
代码
int Pre(int val) { int x,y; SplitByValue(root,val-1,x,y); int now=x,res; while(fhq[now].rc)now=fhq[now].rc; res=fhq[now].val; root=Merge(x,y); return res;}int Aft(int val) { int x,y; SplitByValue(root,val,x,y); int now=y,res; while(fhq[now].lc)now=fhq[now].lc; res=fhq[now].val; root=Merge(x,y); return res;}平衡树的可持久化
可持久化平衡树一般用fhq Treap来实现,一是便于理解,二是也好操作,对应的可持久化操作也大多是添加了版本根节点这个限制而已,具体原理略,见代码
代码(按值)
void SplitByValue(int now,int val,int &x,int &y) {//分裂 if(!now)x=y=0; else { if(fhq[now].val<=val) x=++cnt,fhq[x]=fhq[now],SplitByValue(fhq[x].rc,val,fhq[x].rc,y),Update(x); /*动态开点,如果直接修改,修改的是上一版本, 这里fhq[x]=fhq[now]为初始化左右子节点 */ else y=++cnt,fhq[y]=fhq[now],SplitByValue(fhq[y].lc,val,x,fhq[y].lc),Update(y); }}int Merge(int x,int y) { if(!x||!y)return x+y; int p=++cnt; if(fhq[x].pri>fhq[y].pri) {//按照大根堆的思路合并 fhq[p]=fhq[x]; fhq[p].rc=Merge(fhq[p].rc,y); Update(p); return p; } fhq[p]=fhq[y]; fhq[p].lc=Merge(x,fhq[p].lc); Update(p); return p;}void Insert(int& root,int val) {//需要指明插入的根 int x,y; SplitByValue(root,val,x,y); root=Merge(Merge(x,New(val)),y);}void Delete(int& root,int val) {//需要指明删除的根 int x,y,z; SplitByValue(root,val,x,z); SplitByValue(x,val-1,x,y); y=Merge(fhq[y].lc,fhq[y].rc); root=Merge(Merge(x,y),z);}int GetByRank(int now,int k) { while(now) { if(fhq[fhq[now].lc].num+1==k) return fhq[now].val; if(fhq[fhq[now].lc].num>=k) now=fhq[now].lc; else { k-=fhq[fhq[now].lc].num+1; now=fhq[now].rc; } } return -1;}int GetByValue(int& root,int val) {//需要给出查找的版本根 int x,y,res; SplitByValue(root,val-1,x,y); res=fhq[x].num+1; root=Merge(x,y); return res;}int Pre(int& root,int val) {//需要给出查找的版本根 int x,y; SplitByValue(root,val-1,x,y); if(!x)return -2147483647; int now=x,res; while(fhq[now].rc)now=fhq[now].rc; res=fhq[now].val; root=Merge(x,y); return res;}int Aft(int& root,int val) { int x,y; SplitByValue(root,val,x,y); if(!y)return 2147483647; int now=y,res; while(fhq[now].lc)now=fhq[now].lc; res=fhq[now].val; root=Merge(x,y); return res;}代码(按规模)
int Copy(int p) { int id=New(0); fhq[id]=fhq[p];//预先复制节点 return id;}void Update(int now) {//更新 fhq[now].num=fhq[fhq[now].lc].num+fhq[fhq[now].rc].num+1; fhq[now].sum=fhq[fhq[now].lc].sum+fhq[fhq[now].rc].sum+fhq[now].val;//别忘了加自己}void PushDown(int now) { if(!fhq[now].mark)return ; if(fhq[now].lc)fhq[now].lc=Copy(fhq[now].lc);//左节点存在,复制信息 if(fhq[now].rc)fhq[now].rc=Copy(fhq[now].rc);//同上 swap(fhq[now].lc,fhq[now].rc); fhq[fhq[now].lc].mark^=1; fhq[fhq[now].rc].mark^=1; fhq[now].mark=0;}void SplitBySize(int now,int large,int &x,int &y) { if(!now) { x=y=0; return; } PushDown(now);//如果可以翻转 if(fhq[fhq[now].lc].num<large) { x=New(0);//新版本,需要新开节点 fhq[x]=fhq[now]; SplitBySize(fhq[x].rc,large-fhq[fhq[now].lc].num-1,fhq[x].rc,y); //减去左子树的大小,在右子树中找对应大小的子树接上来 Update(x); } else { y=New(0); fhq[y]=fhq[now]; SplitBySize(fhq[y].lc,large,x,fhq[y].lc); Update(y); }}int Merge(int x,int y) { if(!x||!y)return x+y; if(fhq[x].pri>fhq[y].pri) {//按照大根堆的思路合并 PushDown(x); fhq[x].rc=Merge(fhq[x].rc,y); Update(x); return x; } PushDown(y); fhq[y].lc=Merge(x,fhq[y].lc); Update(y); return y;}void Reverse(int&root,int l,int r) {//区间翻转 int x,y,z; SplitBySize(root,l-1,x,y);//把[1,l-1]拆出来 SplitBySize(y,r-l+1,y,z);//拆长度为r-l+1的区间给y fhq[y].mark^=1; root=Merge(Merge(x,y),z);}void Insert(int& root,int pos,int val) {//单点指定位置插入 int x,y; SplitBySize(root,pos,x,y); root=Merge(x,Merge(New(val),y));}void Delete(int& root,int k) {//单点删除 int x,y,z; SplitBySize(root,k,x,z); SplitBySize(x,k-1,x,y); root=Merge(x,z);}int Query(int&root,int l,int r) {//区间和 int x,y,z; SplitBySize(root,l-1,x,y);//把[1,l-1]拆出来 SplitBySize(y,r-l+1,y,z);//拆长度为r-l+1的区间给y lastans=fhq[y].sum; root=Merge(Merge(x,y),z); return lastans;}训练
LuoguP3369
题目大意:略
思路:权值线段树模板,需要注意特判排名为1的情况和离散化
代码
#include using namespace std;const int maxn=1e5+1;int n,opt[maxn],dic[maxn],a[maxn],cnt;struct data { int id,v; bool operator<(const data&x)const { return v<x.v; }} q[maxn];struct node { int sum;} seg[maxn<<2];void Update(int pos,int v,int l,int r,int rt) { if(l==r) { seg[rt].sum+=v; return ; } int mid=(l+r)/2; if(pos<=mid)Update(pos,v,l,mid,rt<<1); else Update(pos,v,mid+1,r,rt<<1|1); seg[rt].sum=seg[rt<<1].sum+seg[rt<<1|1].sum;}int FindMax(int rt,int l,int r) {//找到当前区间最大值 if(l==r)return l; int mid=(l+r)/2; if(seg[rt<<1|1].sum)return FindMax(rt<<1|1,mid+1,r);//右区间存在 return FindMax(rt<<1,l,mid);}int FindMin(int rt,int l,int r) {//找到区间最小值 if(l==r)return l; int mid=(l+r)/2; if(seg[rt<<1].sum)return FindMin(rt<<1,l,mid);//左区间存在 return FindMin(rt<<1|1,mid+1,r);}int Pre(int v,int rt,int l,int r) {//前驱 if(r<v) {//如果查找值比区间右端点大,代表前驱可能在右区间 if(seg[rt].sum)return FindMax(rt,l,r); return 0; } int mid=(l+r)/2,res;//到这里说明v在[l,r]中 if(mid<v-1&&seg[rt<<1|1].sum&&(res=Pre(v,rt<<1|1,mid+1,r))) return res;//如果比v小的值在右区间,它可能是前驱 return Pre(v,rt<<1,l,mid);//在左区间}int After(int v,int rt,int l,int r) {//后继 if(v<l) { if(seg[rt].sum)return FindMin(rt,l,r); return 0; } int mid=(l+r)/2,res; if(v<mid&&seg[rt<<1].sum&&(res=After(v,rt<<1,l,mid))) return res; return After(v,rt<<1|1,mid+1,r);}int QueryValue(int v,int rt,int l,int r) {//按照值查找 if(r<v)return seg[rt].sum;//v比r大,代表r之前的都比v小 int mid=(l+r)/2,res=0;//到这里就v比r小 res+=QueryValue(v,rt<<1,l,mid);//先在左区间统计 if(mid<v-1)res+=QueryValue(v,rt<<1|1,mid+1,r);//如果v超过了左区间 return res;}int QueryRank(int k,int rt,int l,int r) {//按照排名查找 if(l==r)return l; int mid=(l+r)/2; if(seg[rt<<1].sum>=k)return QueryRank(k,rt<<1,l,mid); //如果左区间个数大于k,代表排名为k的数在左边 else return QueryRank(k-seg[rt<<1].sum,rt<<1|1,mid+1,r); //否则在右区间找排名为k-左区间个数的数}int main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n; for(int i=1; i<=n; i++) {//离线处理 cin >>opt[i]>>q[i].v; q[i].id=i; } sort(q+1,q+1+n);//排序方便离散化 dic[a[q[1].id]=++cnt]=q[1].v; /*q为记录的询问,q[1].id为数值最小的询问对应的编号 a[q[1].id]为询问被离散化成cnt,dic[cnt]为记录询问对应的真实值 */ for(int i=2; i<=n; i++) { if(q[i].v!=q[i-1].v)cnt++; dic[a[q[i].id]=cnt]=q[i].v; } for(int i=1; i<=n; i++) { switch(opt[i]) { case 1: Update(a[i],1,1,cnt,1); break; case 2: Update(a[i],-1,1,cnt,1); break; case 3: a[i]==1?cout <<1<<endl:cout <<QueryValue(a[i],1,1,cnt)+1<<endl; //特判排名为1,a[i]为数值离散化之后的值,即排名 break; case 4: cout <<dic[QueryRank(dic[a[i]],1,1,cnt)]<<endl; //dic[a[i]]为实值,函数返回下标,dic变成实值 break; case 5: cout <<dic[Pre(a[i],1,1,cnt)]<<endl; break; case 6: cout <<dic[After(a[i],1,1,cnt)]<<endl; break; } } return 0;}LuoguP3919
题目大意:略
思路:可持久化数组模板题,不能用rope,数据量比较大
代码
#include #define lc seg[i].ch[0]#define rc seg[i].ch[1]#define Lc seg[j].ch[0]#define Rc seg[j].ch[1]using namespace std;const int maxn=1e6+5;int n,m,rt[maxn],cnt;struct node { int ch[2],val;} seg[maxn*40];void Build(int &i,int l,int r) { i=++cnt; if(l==r) { scanf("%d",&seg[i].val); return ; } int mid=(l+r)>>1; Build(lc,l,mid); Build(rc,mid+1,r);}void Update(int &i,int j,int l,int r,int pos,int v) { i=++cnt; if(l==r) { seg[cnt].val=v; return ; } lc=Lc,rc=Rc; int mid=(l+r)>>1; if(pos<=mid)Update(lc,Lc,l,mid,pos,v); else Update(rc,Rc,mid+1,r,pos,v);}int Query(int i,int l,int r,int pos) { if(l==r) return seg[i].val; int mid=(l+r)>>1; if(pos<=mid) return Query(lc,l,mid,pos); return Query(rc,mid+1,r,pos);}int main() { scanf("%d%d",&n,&m); Build(rt[0],1,n);//建初始树 for(int i=1; i<=m; i++) { int v,loc,val,op; scanf("%d%d%d",&v,&op,&loc); if(op==1) { scanf("%d",&val); Update(rt[i],rt[v],1,n,loc,val); } else { rt[i]=rt[v];//复制 printf("%d\n",Query(rt[v],1,n,loc)); } } return 0;}LuoguP4567
题目大意:略
思路:使用rope实现各自对应的功能即可,但是翻转需要单独实现,由于rope复制是 O ( 1 ) O(1) O(1),所以可以存翻转的串,然后翻转时直接复制即可
代码
#include #include using namespace std;using namespace __gnu_cxx;const int maxn=1<<22+5;int n,cnt;rope<char>a,b,tmp;char now,goal[maxn],bac[maxn];int main() { scanf("%d",&n); getchar();//扫\n while(n--) { char op[20]= {'\0'}; int k,len; scanf("%s",op+1); switch(op[1]) {//判断操作 case 'M': scanf("%d",&k); getchar(); cnt=k; break; case 'I': scanf("%d",&k); getchar();//扫换行 len=a.size(); for(int i=0; i<k; i++)//顺着存和倒着存 bac[k-i-1]=goal[i]=getchar(); goal[k]=bac[k]='\0';//便于输出 a.insert(cnt,goal);//存正的 //cout <<"a:"<<a<<endl; b.insert(len-cnt,bac);//存倒的 //cout <<"b:"<<b<<endl; break; case 'D': scanf("%d",&k); getchar(); len=a.size(); a.erase(cnt,k);//正着删 //cout <<"a:"<<a<<endl; b.erase(len-cnt-k,k);//倒着删 //cout <<"b:"<<b<<endl; break; case 'R': scanf("%d",&k); getchar(); len=a.size(); tmp=a.substr(cnt,k); a=a.substr(0,cnt)+b.substr(len-cnt-k,k)+a.substr(cnt+k,len-cnt-k); //[0,cnt]原先的部分,[len-cnt-l,k]翻转的部分,[cnt+k,len-cnt-k]原先的部分 b=b.substr(0,len-cnt-k)+tmp+b.substr(len-cnt,cnt);// cout <<"a:"<<a<<endl;// cout <<"b:"<<b<<endl; break; case 'G': putchar(a[cnt]); if(a[cnt]!='\n')putchar('\n'); //cout <<"a:"<<a<<endl; break; case 'P': cnt--; break; case 'N': cnt++; break; } } return 0;}LuoguP3402
题目大意:略
思路:可持久化并查集模板题,注意更新当前版本是在上一版本的基础上更新的
代码
#include #define lc seg[i].ch[0]#define rc seg[i].ch[1]#define Lc seg[j].ch[0]#define Rc seg[j].ch[1]using namespace std;const int maxn=2e5+5;int n,m,op,k,a,b,rtfa[maxn],rtdeep[maxn],cnt;struct node { int val,ch[2];} seg[maxn*60];void Build(int&i,int l,int r) {//建树,这里的树是记录父节点树 i=++cnt; if(l==r) { seg[i].val=l; return ; } int mid=(l+r)>>1; Build(lc,l,mid); Build(rc,mid+1,r);}void Update(int&i,int j,int l,int r,int pos,int v) {//这里的树既可以是深度树也可以是父节点树 i=++cnt; seg[i]=seg[j]; if(l==r) { seg[i].val=v; return ; } int mid=(l+r)>>1; if(pos<=mid)Update(lc,Lc,l,mid,pos,v); else Update(rc,Rc,mid+1,r,pos,v);}int Query(int i,int l,int r,int pos) { if(l==r)return seg[i].val; int mid=(l+r)>>1; if(pos<=mid)return Query(lc,l,mid,pos); return Query(rc,mid+1,r,pos);}int Find(int i,int x) { int fx=Query(rtfa[i],1,n,x); return fx==x?x:Find(i,fx);//无路径压缩}void Merge(int i,int x,int y) { x=Find(i-1,x);//找上一版本的祖宗,因为要构造这一版本,当前版本为空 y=Find(i-1,y);//同理 if(x==y) {//属于同一集合,直接复制上版本的所有情况 rtfa[i]=rtfa[i-1]; rtdeep[i]=rtdeep[i-1]; } else {//按秩合并 int dx=Query(rtdeep[i-1],1,n,x);//获得深度 int dy=Query(rtdeep[i-1],1,n,y);//同上 if(dx<dy) { Update(rtfa[i],rtfa[i-1],1,n,x,y);//将i版本x的父节点更新为y rtdeep[i]=rtdeep[i-1];//复制节点 } else if(dx>dy) { Update(rtfa[i],rtfa[i-1],1,n,y,x);//将i版本y的父节点更新为x rtdeep[i]=rtdeep[i-1];//复制节点 } else { Update(rtfa[i],rtfa[i-1],1,n,x,y);//将i版本x的父节点更新为y Update(rtdeep[i],rtdeep[i-1],1,n,y,dy+1);//深度增加 } }}int main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n>>m; Build(rtfa[0],1,n); for(int i=1; i<=m; i++) { cin >>op; switch(op) { case 1: cin >>a>>b; Merge(i,a,b); break; case 2: cin >>k; rtfa[i]=rtfa[k]; rtdeep[i]=rtdeep[k]; break; case 3: cin >>a>>b; rtfa[i]=rtfa[i-1]; rtdeep[i]=rtdeep[i-1]; Find(i,a)==Find(i,b)?cout <<1:cout <<0; cout <<endl; break; } } return 0;}2019南昌A
题目大意:n个节点,现在需要构造一个支持下列五种操作的数据结构
- k a b 合并第k版本的节点a和b
- k a 使第k版本的a删除
- k a b使得第k版本的节点a从当前集合中移出然后与b所在的集合合并
- k a b判断第k版本的节点a是否和结点b在同一个集合中
- 统计第k版本的节点a的子树大小
思路:题意是维护一个可持久化带删并查集,但是由于数据过大,而可持久化并查集的时间复杂度为 O ( n ( log n ) 2 ) O(n(\log n)^2) O(n(logn)2),会超时,因此尝试离线处理,根据操作之间的顺序构建出一个操作图,然后直接处理每一个状态,解决完之后回溯,因为需要回溯,所以用按秩合并,而不能用路径压缩
代码
#include #define ll long long#define INF 0x3f3f3f3fusing namespace std;const int maxn=1e6+50;int n,m,k,f[maxn<<1],sz[maxn<<1],to[maxn],cnt,res[maxn],h[maxn<<1];vector<int>graph[maxn];struct node { int op,a,b;} opt[maxn];int Seek(int x) { return f[x]==x?x:Seek(f[x]);}void DFS(int u) { int op=opt[u].op,a=opt[u].a,b=opt[u].b; if(op==4) { if(to[a]==-1||to[b]==-1)res[u]=0;//如果有一个已经被删除了 else res[u]=(Seek(to[a])==Seek(to[b]));//找虚点是否为一个集合 } else if(op==5) { if(to[a]==-1)res[u]=0;//a被删除了 else res[u]=sz[Seek(to[a])]; } int len=graph[u].size(); for(int i=0; i<len; i++) {//获得邻接的操作 int v=graph[u][i]; op=opt[v].op,a=opt[v].a,b=opt[v].b; if(op==1) {//如果是合并 if(to[a]==-1||to[b]==-1) {//如果有一个被删了 DFS(v); continue; } int fa=Seek(to[a]),fb=Seek(to[b]); if(fa==fb) {//本来就在一个集合中 DFS(v); continue; } if(h[fa]==h[fb]) {//树高相同 f[fb]=fa,sz[fa]+=sz[fb],h[fa]++;//构造 DFS(v);//在此条件下继续 f[fb]=fb,sz[fa]-=sz[fb],h[fa]--;//回溯 } else { if(h[fa]<h[fb])swap(fa,fb); f[fb]=fa,sz[fa]+=sz[fb];//深度小的向深度大的合并 DFS(v); f[fb]=fb,sz[fa]-=sz[fb]; } } else if(op==2) { int t=to[a]; if(to[a]==-1) { DFS(v); continue; } int fa=Seek(to[a]); to[a]=-1; sz[fa]--; DFS(v); to[a]=t; sz[fa]++; } else if(op==3) { if(to[a]==-1||to[b]==-1) { DFS(v); continue; } int fa=Seek(to[a]),fb=Seek(to[b]); if(fa==fb) { DFS(v); continue; } int t=to[a]; to[a]=++cnt; sz[to[a]]=1; sz[fa]--; f[to[a]]=fb; sz[fb]++; DFS(v); sz[fb]--; sz[fa]++; to[a]=t; } else DFS(v); }}int main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n>>m; for(int i=1; i<=m; i++) { int op,k,a,b=0; cin >>op>>k>>a; graph[k].push_back(i);//存图 if(op!=2&&op!=5)cin >>b; opt[i]=(node) {//存询问,便于离线 op,a,b }; } for(int i=1; i<=n; i++)to[i]=i,f[i]=i,sz[i]=1;//初始化 cnt=n; DFS(0);//根据构造好的图来获得每个询问的结果 for(int i=1; i<=m; i++) if(opt[i].op==4) { if(res[i]==0)cout <<"No\n"; else cout <<"Yes\n"; } else if(opt[i].op==5) cout <<res[i]<<endl; return 0;}POJ2104
题目大意:多个询问,每次询问第k版本的区间[l,r]的区间第k小数
思路:可持久化权值线段树模板题
代码
#include #include #include #include #include #define lc seg[i].ch[0]#define rc seg[i].ch[1]#define Lc seg[j].ch[0]#define Rc seg[j].ch[1]using namespace std;const int maxn=1e5+5;int n,m,rt[maxn],a[maxn],b[maxn],cnt;struct node { int num,ch[2]; //这里必须用,因为每个节点的左右子树并不是单个线段树那样简单} seg[maxn*20];void update(int &i,int j,int l,int r,int v) { i=++cnt;//创建新的节点存储区间信息 seg[i]=seg[j];//初始化为上一版本 seg[i].num++;//在这一版本上进行修改 if(l==r)return; int mid=(l+r)>>1; if(v<=mid)update(lc,Lc,l,mid,v); //权值线段树,v即对应的下标增加 else update(rc,Rc,mid+1,r,v);}int query(int i,int j,int l,int r,int v) { if(l==r)return l; int s=seg[Lc].num-seg[lc].num;//计算版本之间的差值 int mid=(l+r)>>1; if(v<=s)return query(lc,Lc,l,mid,v); //类似平衡树,如果区间内的个数比v大,则v必然在区间内 else return query(rc,Rc,mid+1,r,v-s); //否则在区间外}int main() { scanf("%d%d",&n,&m); for(int i=1; i<=n; i++) { scanf("%d",&a[i]); b[i]=a[i]; } sort(b+1,b+1+n);//排序 int tot=unique(b+1,b+n+1)-b-1;//去重 for(int i=1; i<=n; i++) update(rt[i],rt[i-1],1,tot,lower_bound(b+1,b+tot+1,a[i])-b); /*rt[i]为当前版本的根,rt[i-1]为上一个版本的根,1~tot为操作区间 二分查找需要插的值 */ int i,j,k; while(m--) { scanf("%d%d%d",&i,&j,&k); printf("%d\n",b[query(rt[i-1],rt[j],1,tot,k)]); //前缀和的思路,查询 } return 0;}LuoguP4735
题目大意:略
思路:本题为统计最大异或和问题,因存在区间限制,所以用可持久化Trie解决,根据异或的性质,设 s [ i ] = ⊕j=1 i a j s[i]=⊕_{j=1}^i a_j s[i]=⊕j=1iaj,那么 ⊕j=p N a j = s [ p − 1 ] ⊕ s [ N ] ⊕_{j=p}^N a_j=s[p-1]⊕s[N] ⊕j=pNaj=s[p−1]⊕s[N],最后可以得到 ⊕j=p N a j ⊕ x = s [ p − 1 ] ⊕ s [ N ] ⊕ x ⊕_{j=p}^N a_j⊕x=s[p-1]⊕s[N]⊕x ⊕j=pNaj⊕x=s[p−1]⊕s[N]⊕x,那么题干中的询问Ian转换成求解一个 p p p使得 s [ p ] ⊕ s [ N ] ⊕ x s[p]⊕s[N]⊕x s[p]⊕s[N]⊕x最大,求解异或最大,可以将每一个数的异或前缀和按照顺序插入Trie,询问时从树根出发,沿着与询问值相反位的边走即可,如果不能继续,则选择另一条边
在有区间限制的情况下,每个根 r t [ i ] rt[i] rt[i]存储 s [ 0 ] − − > s [ i ] s[0]-->s[i] s[0]−−>s[i]二进制编码,在 r t [ r − 1 ] rt[r-1] rt[r−1]上查询,沿着与当前位相反的边且该节点对应的 s [ ] s[] s[]下标 p p p大小或等于 l − 1 l-1 l−1,这样求出的 p p p满足区间限制
代码
#include using namespace std;const int maxn=6e5+5;int rt[maxn],n,m,s[maxn],cnt,trie[maxn*30][2],maxs[maxn*30];//二进制不超过24位void Insert(int id,int k,int q,int p) { maxs[q]=id;//记录这个点是第几个数的 if(k<0)return ; int c=s[id]>>k&1; if(p)trie[q][c^1]=trie[p][c^1];//如果有值,需要复制 trie[q][c]=++cnt;//必须先复制后赋值,因为可能赋值值被更新 Insert(id,k-1,trie[q][c],trie[p][c]);}int Query(int q,int k,int val,int l) { if(k<0)return s[maxs[q]]^val; int c=val>>k&1; if(maxs[trie[q][c^1]]>=l)return Query(trie[q][c^1],k-1,val,l); //下标不小于l-1 return Query(trie[q][c],k-1,val,l);}/*判断只需要判断下界l-1,因为当前记录的范围为1~r-1,必然不会超过上界,沿着与当前位相反的边走时,可能走向下标小于l-1的节点,与当前位相同的节点不用判断下标,因为必然在当前树中*/int main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n>>m; maxs[0]=-1;//初始化 rt[0]=++cnt;//开新节点 Insert(0,23,rt[0],0);//第1版本 for(int i=1; i<=n; i++) { int x; cin >>x; s[i]=s[i-1]^x;//异或前缀和 rt[i]=++cnt;//开新根 Insert(i,23,rt[i],rt[i-1]);// } char op; int l,r,x; for(int i=1; i<=m; i++) { cin >>op; if(op=='A') { cin >>x; rt[++n]=++cnt; s[n]=s[n-1]^x; Insert(n,23,rt[n],rt[n-1]); } else { cin >>l>>r>>x; cout <<Query(rt[r-1],23,x^s[n],l-1)<<endl; } } return 0;}HDU4348(题目已无法提交)
题目大意:n个整数 a 1 , a 2 … a n a_1,a_2\dots a_n a1,a2…an,实现4种操作
- C l r d:每个 ai ( l ≤ i ≤ r ) a_i(l\le i\le r) ai(l≤i≤r)增加一个常数d d d,时间戳增加
- Q l r:查询对应区间和
- H l r t:查询t时间对应区间和
- B t:回到时间t,一旦回到过去,不能再访问一个前进版
思路:对于可持久化线段树来说,区间更新是大问题,因为可持久化线段树不允许对历史版本更新,因为更新历史版本会引起连锁反应,之后所有的重用该节点的版本都需要更新,所以使用懒标记,查询时不下传,遇到懒标记就累和,最后将懒标记影响加到最后答案里,这是永久化懒标记,因为要计算区间和,所以本题不能使用权值线段树,只能使用普通的可持久化线段树
代码
#include#include#define lc tr[i].ch[0]#define rc tr[i].ch[1]#define Lc tr[j].ch[0]#define Rc tr[j].ch[1]#define mid (l+r>>1) //加括号const int maxn=100005;using namespace std;typedef long long int ll;int n,m;struct node{ int ch[2]; ll sum,lazy;}tr[maxn*20];int cnt,rt[maxn];void push_up(int i){tr[i].sum=tr[lc].sum+tr[rc].sum;}//上推void build(int &i,int l,int r){ i=++cnt;//动态开点 tr[i].lazy=0; if(l==r){ scanf("%lld",&tr[i].sum); return; } build(lc,l,mid); build(rc,mid+1,r); push_up(i);}void update(int &i,int j,int l,int r,int L,int R,int c){ i=++cnt;//动态开点 tr[i]=tr[j];//查询过程中复制经过的节点 tr[i].sum+=1ll*(R-L+1)*c; if(l>=L&&r<=R){ tr[i].lazy+=c; return; }//注意,没有下推函数 if(R<=mid) update(lc,Lc,l,mid,L,R,c); else if(L>mid) update(rc,Rc,mid+1,r,L,R,c); else{ update(lc,Lc,l,mid,L,mid,c);update(rc,Rc,mid+1,r,mid+1,R,c); }}ll query(int i,int l,int r,int L,int R,ll x){ if(l>=L&&r<=R) return tr[i].sum+1ll*(r-l+1)*x;//返回节点和值+区间长度×懒标记 if(R<=mid) return query(lc,l,mid,L,R,x+tr[i].lazy); else if(L>mid) return query(rc,mid+1,r,L,R,x+tr[i].lazy); else return query(lc,l,mid,L,mid,x+tr[i].lazy)+query(rc,mid+1,r,mid+1,R,x+tr[i].lazy);}int main(){char op[2]; while(~scanf("%d%d",&n,&m)){ cnt=0; int now=0; build(rt[0],1,n); while(m--){ int l,r,d,t; scanf("%s",op); if(op[0]=='Q'){ scanf("%d%d",&l,&r); printf("%lld\n",query(rt[now],1,n,l,r,0)); } else if(op[0]=='H'){ scanf("%d%d%d",&l,&r,&t); printf("%lld\n",query(rt[t],1,n,l,r,0)); } else if(op[0]=='B'){ scanf("%d",&t); now=t;//回到历史版本直接赋值即可,但是需要将后面的版本都去掉 cnt=rt[t+1]-1;//没有此句会浪费5倍空间! //重置节点下标cnt为t版本的最后一个节点编号 } else{ scanf("%d%d%d",&l,&r,&d); now++; update(rt[now],rt[now-1],1,n,l,r,d); } } } return 0;}SP10628
题目大意:略
思路:首先需要对权值离散化,由于涉及到树上路径,需要求LCA,设 f ( u , a , b ) f(u,a,b) f(u,a,b)为根节点到 u u u路径上点权落在 [ a , b ] [a,b] [a,b]中的点的个数,设 g ( u , v , a , b ) g(u,v,a,b) g(u,v,a,b)为 u − > v u->v u−>v路径上点权在区间 [ a , b ] [a,b] [a,b]的点个数,那么可以求得 g ( u , v , a , b ) = f ( u , a , b ) + f ( v , a , b ) − f ( l c a ( a , b ) , a , b ) − f ( f a ( l c a ( a , b ) ) , a , b ) g(u,v,a,b)=f(u,a,b)+f(v,a,b)-f(lca(a,b),a,b)-f(fa(lca(a,b)),a,b) g(u,v,a,b)=f(u,a,b)+f(v,a,b)−f(lca(a,b),a,b)−f(fa(lca(a,b)),a,b),这是树上差分的思路,具体解释如图,假如现在要算 u − > v u->v u−>v路径上的和,那么这个和就可以通过如下过程得来:
s u m ( r o o t , l c a ) = r o o t + f l c a + l c a sum(root,lca)=root+flca+lca sum(root,lca)=root+flca+lca
s u m ( r o o t , f l c a ) = r o o t + f l c a sum(root,flca)=root+flca sum(root,flca)=root+flca
s u m ( r o o t , u ) = r o o t + f l c a + l c a + u sum(root,u)=root+flca+lca+u sum(root,u)=root+flca+lca+u
s u m ( r o o t , v ) = r o o t + f l c a + l c a + v sum(root,v)=root+flca+lca+v sum(root,v)=root+flca+lca+v
那么可以得到s u m ( u , v ) = s u m ( r o o t , u ) + s u m ( r o o t , v ) − s u m ( r o o t , f l c a ) − s u m ( r o o t , l c a ) sum(u,v)=sum(root,u)+sum(root,v)-sum(root,flca)-sum(root,lca) sum(u,v)=sum(root,u)+sum(root,v)−sum(root,flca)−sum(root,lca)
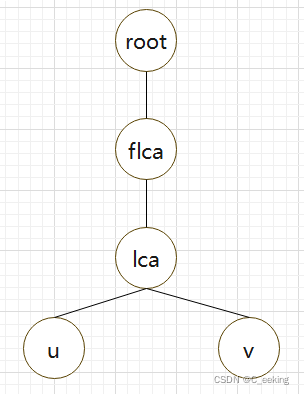
对于查询的区间进行二分,如果 g ( u , v , 1 , n / 2 ) ≥ k g(u,v,1,n/2)\ge k g(u,v,1,n/2)≥k,k为需要查询的排名,那么k一定在 [ 1 , n / 2 ] [1,n/2] [1,n/2]中,递归查找即可,那么现在关键的地方就是求解 f ( u , a , b ) f(u,a,b) f(u,a,b),也就是根节点到 u u u路径上的权值和,那么,可以对每个点开一个权值线段树,记录各区间的点权出现次数,但是需要注意的一点是,每个节点的权值线段树是相对于父节点更新的,也就是在构造可持久化线段树时,对于每一棵可持久化线段树,其实是记录了一条链上的区间情况,本题必须用树链剖分
代码
#include #pragma GCC optimize(2)//#define int long long#define lc seg[i].ch[0]#define rc seg[i].ch[1]#define Lc seg[j].ch[0]#define Rc seg[j].ch[1]using namespace std;const int maxn=1e5+5;int n,m,ans,cnt,rt[maxn],head[maxn],val[maxn],b[maxn],len;int fa[maxn],son[maxn],Size[maxn],d[maxn],level,top[maxn];struct node { int next,to;} e[maxn<<1];void Add(int from,int to) { e[++cnt].to=to; e[cnt].next=head[from]; head[from]=cnt;}void DFS1(int u,int f) { Size[u]=1; d[u]=d[f]+1;//子树大小,点深度 son[u]=0; fa[u]=f;//重链节点,父节点 for(int i=head[u]; ~i; i=e[i].next ) { int v=e[i].to; if(v==f)continue; DFS1(v,u); Size[u]+=Size[v]; if(Size[son[u]]<Size[v]) son[u]=v; }}void DFS3(int u,int topu) { top[u]=topu; if(son[u])DFS3(son[u],topu); for(int i=head[u]; ~i; i=e[i].next) if(e[i].to!=fa[u]&&e[i].to!=son[u]) DFS3(e[i].to,e[i].to);//开启一条新重链}int LCA(int x,int y) { while(top[x]!=top[y]) { //不在同一重链时 if(d[top[x]]<d[top[y]])//确保x的top深度更大 swap(x,y); x=fa[top[x]];//x往上跳过一条轻边 } return d[x]<d[y]?x:y;//返回深度小的}struct p { int val,ch[2];} seg[maxn*20];void Update(int &i,int j,int l,int r,int v) { i=++ans;//创建新的节点存储区间信息 seg[i]=seg[j];//初始化为上一版本 seg[i].val++;//在这一版本上进行修改 if(l==r)return; int mid=(l+r)>>1; if(v<=mid)Update(lc,Lc,l,mid,v); //权值线段树,v即对应的下标增加 else Update(rc,Rc,mid+1,r,v);}int QuerySum(int i,int j,int l,int r,int L,int R) { if(l>=L&&r<=R)return seg[i].val-seg[j].val; int mid=(l+r)>>1,res=0; if(L<=mid)res+=QuerySum(lc,Lc,l,mid,L,R);//必须逐个判断这样写 if(R>mid)res+=QuerySum(rc,Rc,mid+1,r,L,R); return res;}int Query(int u,int v,int l,int r,int k) {//询问 if(l==r)return l; int lca=LCA(u,v),f=fa[lca],mid=(l+r)>>1; int g=QuerySum(rt[u],rt[0],1,len,l,mid);//树上差分 g+=QuerySum(rt[v],rt[0],1,len,l,mid); g-=QuerySum(rt[lca],rt[0],1,len,l,mid); g-=QuerySum(rt[f],rt[0],1,len,l,mid); if(g>=k) return Query(u,v,l,mid,k);//原理类似于平衡树 return Query(u,v,mid+1,r,k-g);}void DFS2(int u) { Update(rt[u],rt[fa[u]],1,len,lower_bound(val+1,val+len+1,b[u])-val); for(int i=head[u]; ~i; i=e[i].next) { int v=e[i].to; if(fa[u]==v)continue; DFS2(v); }}int main() { scanf("%d%d",&n,&m); memset(head,-1,sizeof(head)); for(int i=1; i<=n; i++) {//读入 scanf("%d",&val[i]); b[i]=val[i];//复制一遍,便于插入 } sort(val+1,val+1+n); len=unique(val+1,val+1+n)-val-1;//排序与离散化 for(int i=0; i<n-1; i++) {//建树 int u,v; scanf("%d%d",&u,&v); Add(u,v); Add(v,u); } d[1]=1;//第一个必须为1,不然1和0的深度就相同了 DFS1(1,0); DFS3(1,1); DFS2(1); while(m--) { int u,v,p; scanf("%d%d%d",&u,&v,&p); printf("%d\n",val[Query(u,v,1,len,p)]); } return 0;}/*8 41 2 3 4 5 6 7 81 21 31 42 52 63 73 81 5 25 8 14 5 27 8 2*/UVA12538
题目大意:略
思路:正解应该是可持久化平衡树,但是由于数据量很小(5e4),所以可以用rope直接暴力存储和更新
代码
#include #include using namespace std;using namespace __gnu_cxx;const int maxn=5e4+5;int n,c,len;crope now,s[maxn];//在线处理和存储版本结果char str[maxn];//crope等价ropeint main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n; for(int i=1; i<=n; i++) { int op,pos,x,v; crope res; cin >>op; switch(op) { case 1: cin >>pos; cin >>str; pos-=c; now.insert(pos,str); s[++len]=now; break; case 2: cin >>pos>>x; pos-=c,x-=c; now.erase(pos-1,x); s[++len]=now; break; default: cin >>v>>pos>>x; v-=c,pos-=c,x-=c; res=s[v].substr(pos-1,x); c+=count(res.begin(),res.end(),'c'); cout <<res<<endl; break; } } return 0;}UVA11987
题目大意:有多个元素,构造支持下列三种操作的数据结构
- 合并 p q所在集合
- 将p从所在集合摘下,合并到q所在集合
- 输出p所在集合大小以及集合元素和
思路:带删并查集模板题
代码
#include using namespace std;const int maxn=2e5+5;int n,m,fa[maxn],siz[maxn],sum[maxn],op,p,q,fp,fq;int Seek(int x) { return fa[x]==x?x:Seek(fa[x]);}void Union(int x,int y) { int fx=Seek(x),fy=Seek(y); if(fx!=fy) fa[fx]=fy; siz[fy]+=siz[fx];//统计子树大小 sum[fy]+=sum[fx];//统计子树和}int main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n>>m; for(int i=1; i<=n; i++)//初始化父节点 fa[i]=i+n; for(int i=n+1; i<=2*n; i++) { fa[i]=i; siz[i]=1;//初始化 sum[i]=i-n;//初始化 } while(m--) { cin >>op; switch(op) { case 1: cin >>p>>q; Union(p,q); break; case 2: cin >>p>>q; fp=Seek(p),fq=Seek(q); if(fp==fq)continue; fa[p]=fq;//这里修改的不是根节点 siz[fp]--,siz[fq]++; sum[fp]-=p,sum[fq]+=p; break; case 3: cin >>p; cout <<siz[Seek(p)]<<" "<<sum[Seek(p)]<<endl; break; } } return 0;}LuoguP4359
题目大意:略
思路:首先,题目给的数据量很大,但是分析题目给出的条件: a k k ≤ N , a k < 128 a_k^k\le N,a_k\lt 128 akk≤N,ak<128, N N N到达了 1 0 18 10^{18} 1018,那么k就不会超过8,也就是说,符合题目条件的数很少,对于给出的N,可以预处理一下满足条件的 a k k a_k^k akk(注意k是项数,不是种数),那么求前k大的数即可,显然所有满足条件的 a k k a_k^k akk并不是全部的数,比如可以将 a k k a_k^k akk替换成 a kk−1 ak−1 a_k^{k-1}a_{k-1} akk−1ak−1,这个数肯定是比 ak−1 k a_{k-1}^k ak−1k大的,那么用堆来维护所有的数,每次获得最大的数,并且尝试将最大的数替换某一项进行缩小再放入堆中,取K次即可
PS: 本题可以用可持久化左偏树来做,但是看了更多的题解之后还是堆+贪心更简单且更容易理解
代码
#include #define int long longusing namespace std;int n,k,prime[200],cnt;struct node { int v,t,pre,p; //初始为最大质因子的k次方,实际上是这个数的值 //最大质因子有几个 //次大质因子下标,最大质因子下标 bool operator<(const node&a)const { return v<a.v; }};priority_queue<node>q;signed main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n>>k; prime[++cnt]=2; for(int i=3; i<128; i+=2) {//预处理2~127的质数 bool flag=0; for(int j=2; j<=i/j; j++) if(i%j==0) { flag=1; break; } if(!flag)prime[++cnt]=i; } for(int i=1; i<=cnt; i++) for(int t=1,j=1; t*prime[i]<=n; j++) { t*=prime[i];//构造这个数 q.push({t,j,i-1,i}); } node tmp; while(k--) {//拿前K大个 tmp=q.top(); q.pop(); if(tmp.t>1)//如果最大质因子个数大于1,尝试用次大或更小的替换 for(int i=tmp.pre; i; i--) q.push({tmp.v/prime[tmp.p]*prime[i],tmp.t-1,i,tmp.p}); //更新这个数,用次大质因子/更小的质因子替换,最大质因子个数减少 //次大质因子下标,最大质因子下标 } cout <<tmp.v; return 0;}LuoguP3391
题目大意:略
思路:平衡树区间操作模板题,可以用Splay,也可以用fhq Treap
代码
#include using namespace std;const int maxn=4e5+5;int cnt,root;struct node { int val,pri,lc,rc,num; bool mark;} fhq[maxn];inline int New(int v) { fhq[++cnt].val=v; fhq[cnt].lc=fhq[cnt].rc=0; fhq[cnt].num=1; fhq[cnt].pri=rand(); fhq[cnt].mark=0;//标记是否需要翻转 return cnt;}void Update(int now) {//向上更新 fhq[now].num=fhq[fhq[now].lc].num+fhq[fhq[now].rc].num+1;}void PushDown(int now) {//向下更新 swap(fhq[now].lc,fhq[now].rc);//先翻转区间 fhq[fhq[now].lc].mark^=1;//打标记 fhq[fhq[now].rc].mark^=1; fhq[now].mark=0;}void SplitBySize(int now,int large,int &x,int &y) { if(!now)x=y=0; else { if(fhq[now].mark)PushDown(now);//如果可以翻转 if(fhq[fhq[now].lc].num<large) { x=now; SplitBySize(fhq[now].rc,large-fhq[fhq[now].lc].num-1,fhq[now].rc,y); //减去左子树的大小,在右子树中找对应大小的子树接上来 } else { y=now; SplitBySize(fhq[now].lc,large,x,fhq[now].lc); } Update(now); }}int Merge(int x,int y) { if(!x||!y)return x+y; if(fhq[x].pri>fhq[y].pri) { if(fhq[x].mark)PushDown(x); fhq[x].rc=Merge(fhq[x].rc,y); Update(x); return x; } if(fhq[y].mark)PushDown(y); fhq[y].lc=Merge(x,fhq[y].lc); Update(y); return y;}void Reverse(int l,int r) { int x,y,z; SplitBySize(root,l-1,x,y);//把[1,l-1]拆出来 SplitBySize(y,r-l+1,y,z);//拆长度为r-l+1的区间给y fhq[y].mark^=1; root=Merge(Merge(x,y),z);}void Print(int now) { if(!now)return ; if(fhq[now].mark)PushDown(now); Print(fhq[now].lc); cout <<fhq[now].val<<" "; Print(fhq[now].rc);}int main() { ios::sync_with_stdio(0); cin.tie(0); int n,m; cin >>n>>m; for(int i=1; i<=n; i++) root=Merge(root,New(i)); while(m--) { int l,r; cin >>l>>r; Reverse(l,r); } Print(root); return 0;}LuoguP3835
题目大意:略
思路:可持久化平衡树单点修改模板题
代码
#include using namespace std;const int maxn=5e5+5;int n,rt[maxn],cnt,v,op,x;struct node { int val,lc,rc,pri,num;} fhq[maxn*60];inline int New(int v) {//新节点 fhq[++cnt].val=v; fhq[cnt].lc=fhq[cnt].rc=0; fhq[cnt].num=1;//子树大小 fhq[cnt].pri=rand(); return cnt;}void Update(int now) {//更新 fhq[now].num=fhq[fhq[now].lc].num+fhq[fhq[now].rc].num+1;}void SplitByValue(int now,int val,int &x,int &y) {//分裂 if(!now)x=y=0; else { if(fhq[now].val<=val) x=++cnt,fhq[x]=fhq[now],SplitByValue(fhq[x].rc,val,fhq[x].rc,y),Update(x); /*动态开点,如果直接修改,修改的是上一版本, 这里fhq[x]=fhq[now]为初始化左右子节点 */ else y=++cnt,fhq[y]=fhq[now],SplitByValue(fhq[y].lc,val,x,fhq[y].lc),Update(y); }}int Merge(int x,int y) { if(!x||!y)return x+y; int p=++cnt; if(fhq[x].pri>fhq[y].pri) {//按照大根堆的思路合并 fhq[p]=fhq[x]; fhq[p].rc=Merge(fhq[p].rc,y); Update(p); return p; } fhq[p]=fhq[y]; fhq[p].lc=Merge(x,fhq[p].lc); Update(p); return p;}void Insert(int& root,int val) {//需要指明插入的根 int x,y; SplitByValue(root,val,x,y); root=Merge(Merge(x,New(val)),y);}void Delete(int& root,int val) {//需要指明删除的根 int x,y,z; SplitByValue(root,val,x,z); SplitByValue(x,val-1,x,y); y=Merge(fhq[y].lc,fhq[y].rc); root=Merge(Merge(x,y),z);}int GetByRank(int now,int k) { while(now) { if(fhq[fhq[now].lc].num+1==k) return fhq[now].val; if(fhq[fhq[now].lc].num>=k) now=fhq[now].lc; else { k-=fhq[fhq[now].lc].num+1; now=fhq[now].rc; } } return -1;}int GetByValue(int& root,int val) {//需要给出查找的版本根 int x,y,res; SplitByValue(root,val-1,x,y); res=fhq[x].num+1; root=Merge(x,y); return res;}int Pre(int& root,int val) {//需要给出查找的版本根 int x,y; SplitByValue(root,val-1,x,y); if(!x)return -2147483647; int now=x,res; while(fhq[now].rc)now=fhq[now].rc; res=fhq[now].val; root=Merge(x,y); return res;}int Aft(int& root,int val) { int x,y; SplitByValue(root,val,x,y); if(!y)return 2147483647; int now=y,res; while(fhq[now].lc)now=fhq[now].lc; res=fhq[now].val; root=Merge(x,y); return res;}int main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n; for(int i=1; i<=n; i++) { cin >>v>>op>>x; rt[i]=rt[v]; switch(op) { case 1: Insert(rt[i],x); break; case 2: Delete(rt[i],x); break; case 3: cout <<GetByValue(rt[i],x)<<endl; break; case 4: cout <<GetByRank(rt[i],x)<<endl; break; case 5: cout <<Pre(rt[i],x)<<endl; break; case 6: cout <<Aft(rt[i],x)<<endl; break; } } return 0;}LuoguP5055
题目大意:略
思路:可持久化平衡树模板题,由于翻转的本质还是对序列修改,所以要在翻转前保存序列
代码
#include #define int long longusing namespace std;const int maxn=5e5+5;int n,rt[maxn],cnt,v,op,x,lastans;struct node { int val,lc,rc,pri,num,mark,sum;} fhq[maxn*60];inline int New(int v) {//新节点 fhq[++cnt].val=v; fhq[cnt].lc=fhq[cnt].rc=0; fhq[cnt].num=1;//子树大小 fhq[cnt].sum=v;//子树和 fhq[cnt].pri=rand(); fhq[cnt].mark=0; return cnt;}int Copy(int p) { int id=New(0); fhq[id]=fhq[p];//预先复制节点 return id;}void Update(int now) {//更新 fhq[now].num=fhq[fhq[now].lc].num+fhq[fhq[now].rc].num+1; fhq[now].sum=fhq[fhq[now].lc].sum+fhq[fhq[now].rc].sum+fhq[now].val;//别忘了加自己}void PushDown(int now) { if(!fhq[now].mark)return ; if(fhq[now].lc)fhq[now].lc=Copy(fhq[now].lc);//左节点存在,复制信息 if(fhq[now].rc)fhq[now].rc=Copy(fhq[now].rc);//同上 swap(fhq[now].lc,fhq[now].rc); fhq[fhq[now].lc].mark^=1; fhq[fhq[now].rc].mark^=1; fhq[now].mark=0;}void SplitBySize(int now,int large,int &x,int &y) { if(!now) { x=y=0; return; } PushDown(now);//如果可以翻转 if(fhq[fhq[now].lc].num<large) { x=New(0);//新版本,需要新开节点 fhq[x]=fhq[now]; SplitBySize(fhq[x].rc,large-fhq[fhq[now].lc].num-1,fhq[x].rc,y); //减去左子树的大小,在右子树中找对应大小的子树接上来 Update(x); } else { y=New(0); fhq[y]=fhq[now]; SplitBySize(fhq[y].lc,large,x,fhq[y].lc); Update(y); }}int Merge(int x,int y) { if(!x||!y)return x+y; if(fhq[x].pri>fhq[y].pri) {//按照大根堆的思路合并 PushDown(x); fhq[x].rc=Merge(fhq[x].rc,y); Update(x); return x; } PushDown(y); fhq[y].lc=Merge(x,fhq[y].lc); Update(y); return y;}void Reverse(int&root,int l,int r) { int x,y,z; SplitBySize(root,l-1,x,y);//把[1,l-1]拆出来 SplitBySize(y,r-l+1,y,z);//拆长度为r-l+1的区间给y fhq[y].mark^=1; root=Merge(Merge(x,y),z);}void Insert(int& root,int pos,int val) { int x,y; SplitBySize(root,pos,x,y); root=Merge(x,Merge(New(val),y));}void Delete(int& root,int k) { int x,y,z; SplitBySize(root,k,x,z); SplitBySize(x,k-1,x,y); root=Merge(x,z);}int Query(int&root,int l,int r) { int x,y,z; SplitBySize(root,l-1,x,y);//把[1,l-1]拆出来 SplitBySize(y,r-l+1,y,z);//拆长度为r-l+1的区间给y lastans=fhq[y].sum; root=Merge(Merge(x,y),z); return lastans;}signed main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n; for(int i=1; i<=n; i++) { int v,opt,x,p; cin >>v>>opt; rt[i]=rt[v]; switch(opt) { case 1: cin >>p>>x; p^=lastans; x^=lastans; Insert(rt[i],p,x); break; case 2: cin >>p; p^=lastans; Delete(rt[i],p); break; case 3: cin >>p>>x; p^=lastans; x^=lastans; Reverse(rt[i],p,x); break; case 4: cin >>p>>x; p^=lastans; x^=lastans; cout <<Query(rt[i],p,x)<<endl; break; } } return 0;}LuoguP4592
题目大意:略
思路:该题和Count on a Tree的思路大体相同,不过是求路径和改成了求异或最大值,该题的实质都是区间查询,对于查询路径,所需要的可持久化Trie和Count on a Tree一样,以父节点之间关系来建树,查询时拆成两条链即可,对于查询子树,可以用树剖,也可以用DFS序,DFS序入序-1到出序这一段即为子树
本题的查询并不简单,因为求的是最值问题而不是求和问题,对于每一个二进制位,我们需要统计其子树大小,为什么呢?因为这个子树大小就代表了从第一个数到当前数中有多少个数在这一位上有1/0,每一次查询同时从后版本和前版本进行遍历,如果后版本在某一位上的子树大小大于前版本,代表至少存在一个数可以使得这一位答案为1(异或结果),以此类推,详见代码
代码
#include using namespace std;const int maxn=1e5+5;int n,q,v[maxn],ans,cnt,head[maxn],dfn,rtdfn[maxn],rtf[maxn],level;int trie[maxn*70][2],in[maxn],out[maxn],fa[maxn][17],d[maxn],sz[maxn*70];struct node { int next,to;} e[maxn<<1];void Add(int from,int to) { e[++cnt].next=head[from]; e[cnt].to=to; head[from]=cnt;}void Insert(int &root,int val,int k) { trie[++ans][0]=trie[root][0];//动态开点 trie[ans][1]=trie[root][1]; sz[ans]=sz[root]+1;//只有一个相同(要么0,要么1),必然会多了一个点 root=ans; if(~k)Insert(trie[root][val>>k&1],val,k-1);}void DFS(int u,int f) { in[u]=++dfn; fa[u][0]=f; d[u]=d[f]+1; level=max(level,d[u]);//获得树的层数 Insert(rtdfn[dfn]=rtdfn[dfn-1],v[u],29);//按照DFS序来构造字典树 Insert(rtf[u]=rtf[f],v[u],29);//按照父节点继承构造字典树 for(int i=head[u]; ~i; i=e[i].next) { int v=e[i].to; if(v==f)continue; DFS(v,u); } out[u]=dfn;//记录DFS出序}void ST() {//没问题 level=log2(level); for(int j=1; j<=level; j++) for(int i=1; i<=n; i++) fa[i][j]=fa[fa[i][j-1]][j-1];}int LCA(int x,int y) {//没问题 if(d[x]>d[y]) swap(x,y); for(int i=level; i>=0; i--) if(d[fa[y][i]]>=d[x]) y=fa[y][i]; if(x==y) return x; for(int i=level; i>=0; i--) if(fa[y][i]!=fa[x][i]) y=fa[y][i],x=fa[x][i]; return fa[y][0];}int Query(int rt1,int rt2,int val,int k) {//rt1为后版本,rt2为前版本 if(k<0)return 0; int c=val>>k&1; if(sz[trie[rt1][c^1]]>sz[trie[rt2][c^1]]) return Query(trie[rt1][c^1],trie[rt2][c^1],val,k-1)|1<<k; //如果后版本在这一位可以选择,即有多的数可以得到c^1,那么这一位答案可以取1 return Query(trie[rt1][c],trie[rt2][c],val,k-1); //否则尝试下一位}int main() { ios::sync_with_stdio(0); cin.tie(0); cin >>n>>q; memset(head,-1,sizeof(head)); for(int i=1; i<=n; i++)//录入数据 cin >>v[i]; for(int i=0; i<n-1; i++) {//建树 int u,v; cin >>u>>v; Add(u,v); Add(v,u); } DFS(1,0);//深搜获得两种不同参考下的可持久化字典树 ST();//构造ST方便求LCA for(int i=1,op,x,y,z; i<=q; i++) { cin >>op; if(op==1) { cin >>x>>z; cout <<Query(rtdfn[out[x]],rtdfn[in[x]-1],z,29)<<endl; //DFS序特性,in[x]-1~out[x]为子树范围 } else { cin >>x>>y>>z; int lcaf=fa[LCA(x,y)][0];//路径分成两个链 cout <<max(Query(rtf[x],rtf[lcaf],z,29),Query(rtf[y],rtf[lcaf],z,29))<<endl; } } return 0;}总结
可持久化与其说是一种算法,更确切的来说是一种思想,几乎所有的可持久化数据结构都用到了动态开点,结点复用,版本开根的思想,只有在对基本的数据结构理解后,才能更好的理解各种可持久化的数据结构,可持久化数据结构适用于要求版本回溯的题目,或者要求在插入序列过程中的区间询问问题(例如区间第k大),总之是一个较难理解与掌握的知识点
参考文献
- 【AgOHの数据结构】可持久化数组
- 【AgOHの数据结构】主席树
- 【算法讲堂】【电子科技大学】【ACM】权值线段树与主席树
- 【权值线段树】bzoj3224 Tyvj 1728 普通平衡树
- [黑科技]__gnu_cxx::rope STL中的可持久化数组
- P4567 [AHOI2006]文本编辑器 题解
- Count on a tree 【SPOJ - COT】【树上第K小、可持久化线段树(主席树)】
- P3919 【模板】可持久化线段树 1(可持久化数组) 题解
- 可持久化线段树 主席树 详解
- 【AgOHの数据结构】可持久化并查集
- 【bzoj4524】【CQOI2016】【伪光滑数】【堆+贪心】
- 【AgOHの数据结构】平衡树专题之贰 fhq Treap(无旋Treap)
- 2019 ICPC 南昌 Regional A. 9102(离线处理 && 带删并查集)
- P4592 [TJOI2018]异或 题解


