SAR笔记-卫星轨迹（三维建模）

文档中心

SAR系列文章目录

《SAR笔记-卫星轨道建模》介绍了ECI（地心惯性坐标系）坐标下卫星轨道的二维建模。这节内容介绍卫星轨道的三维建模，绘制ECI下卫星运行轨迹，ECR（地心地固坐标系）下卫星轨迹以及ECR下卫星星下点轨迹。

SAR系列文章目录

前言

一、位置矢量旋转

1.1 位置矢量绕x轴旋转

1.2 位置矢量绕y轴旋转

1.3 位置矢量绕z轴旋转

二、坐标系旋转

2.1 坐标系绕x轴旋转

2.2 坐标系绕y轴旋转

2.3 坐标系绕z轴旋转

三、卫星轨迹建立

3.1 轨道六根数

3.2 卫星轨迹构建

3.3 仿真结果

总结

前言

绘制卫星轨道的三维轨迹图关键是：位置矢量的旋转；坐标系的旋转。

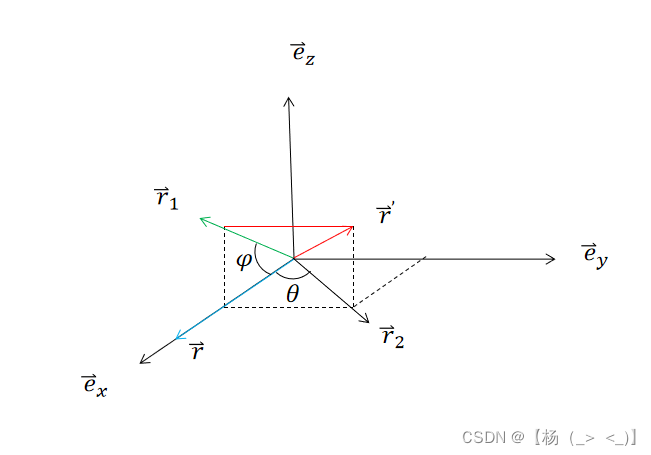
一、位置矢量旋转

位于x轴的位置矢量 $\vec{r}$ 绕坐标原点旋转到坐标系中任意位置矢量 ${\vec{r}}'$ 可以等效为：位置矢量 $\vec{r}$ 绕y轴的瞬时针（迎着y轴看去，下同）旋转 $\varphi$ 角度到达位置矢量 $\vec{r}_{1}$ 处，再由位置矢量 $\vec{r}_{1}$ 绕z轴逆时针旋转 $\theta$ 角度，到达位置矢量 ${\vec{r}}'$ 。或者，位置矢量 $\vec{r}$ 绕z轴的逆时针旋转 $\theta$ 角度到达位置矢量 $\vec{r}_{2}$ 处，再由位置矢量 $\vec{r}_{2}$ 绕y轴逆时针 $\varphi$ 角度，到达位置矢量 ${\vec{r}}'$ 。

同理任意位置矢量可以同时反向旋转回到x轴方向，任意位置矢量可以先通过反向旋转到达x轴，再由x轴旋转到其他任意方向。因此任意位置矢量旋转到其他方向，可以由位置矢量绕x轴，绕y轴，绕z轴旋转得到。

1.1 位置矢量绕x轴旋转

旋转后的位置矢量

${\vec{r}}'=\begin{bmatrix} x0 \\ r\cos \left ( \alpha +\gamma \right )\\ r\sin \left ( \alpha +\gamma \right ) \end{bmatrix}$

展开化简有：

${\vec{r}}'=\begin{bmatrix} x0 \\ r\cos \gamma \cos \alpha -r\sin \gamma \sin \alpha \\ r\sin \gamma \cos \alpha +r\cos \gamma \sin \alpha \end{bmatrix} =\begin{bmatrix} 1& 0 &0 \\ 0& \cos \gamma &-\sin \gamma \\ 0 &\sin \gamma &\cos \gamma \end{bmatrix} \begin{bmatrix} x0 \\ r\cos \alpha \\ r\sin \alpha \end{bmatrix}$

定义绕x轴旋转 $\gamma$ 角度的旋转矩阵为：

$R_{x}\left ( \gamma \right )=\begin{bmatrix} 1& 0 &0 \\ 0& \cos \gamma &-\sin \gamma \\ 0 &\sin \gamma &\cos \gamma \end{bmatrix}$

由此可以通过旋转矩阵 $R_{x}\left ( \gamma \right )$ 与位置矢量 ${\vec{r}}$ 的相乘表示位置矢量 ${\vec{r}}$ 绕x轴旋转 $\gamma$ 角度后的位置矢量

1.2 位置矢量绕y轴旋转

同理有：

${\vec{r}}'=\begin{bmatrix} r\cos \varphi \sin \alpha+r\sin \varphi \cos \alpha \\ y0\\ -r\sin \varphi \sin \alpha+r\cos \varphi \cos \alpha \\ \end{bmatrix} =\begin{bmatrix} \cos \varphi & 0 &\sin \varphi \\ 0& 1 &0 \\ -\sin \varphi &0 &\cos \varphi \end{bmatrix} \begin{bmatrix} r\sin \alpha \\ y0 \\ r\cos \alpha \end{bmatrix}$

绕y轴旋转 $\varphi$ 角度的旋转矩阵为：

$R_{y}\left ( \varphi \right )=\begin{bmatrix} \cos \varphi & 0 &\sin \varphi \\ 0& 1 &0 \\ -\sin \varphi &0 &\cos \varphi \end{bmatrix}$

1.3 位置矢量绕z轴旋转

同理有：

${\vec{r}}'=\begin{bmatrix} r\cos \theta \cos \alpha -r\sin \theta \sin \alpha\\ r\sin \theta \cos \alpha + r\cos \theta \sin \alpha \\ z0\\ \end{bmatrix} =\begin{bmatrix} \cos \theta & -\sin \theta &0\\ \sin \theta & \cos \theta &0 \\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} r\cos \alpha \\ r\sin \alpha \\ z0 \end{bmatrix}$

绕z轴旋转 $\theta$ 角度的旋转矩阵为：

$R_{z}\left ( \theta \right )=\begin{bmatrix} \cos \theta & -\sin \theta &0\\ \sin \theta & \cos \theta &0 \\ 0 &0 &1 \end{bmatrix}$

二、坐标系旋转

卫星轨迹计算是再地心惯性坐标系（ECI）下进行的，最后需要转换的地心地固坐标系（ECR）下。ECR绕坐标相对ECI坐标绕地球自转轴旋转，这里简单介绍坐标系旋转对位置矢量的影响。

2.1 坐标系绕x轴旋转

位置矢量在原坐标系下的表达式：

$\vec{r}=x_{0}\vec{e_{x}}+r\cos \alpha \vec{e_{y}}+r\sin \alpha \vec{e_{y}}\, \, \, \, \, \, \, \, (1)$

原坐标轴在旋转后的坐标轴上的表达式：

$\left\{\begin{matrix} \vec{e}_{x}=\vec{e}_{x}^{'}\\ \vec{e}_{y}=\cos \gamma \vec{e}_{y}^{'}-\sin \gamma \vec{e}_{z}^{'}\\ \vec{e}_{z}=\sin \gamma \vec{e}_{y}^{'}+\cos \gamma \vec{e}_{z}^{'} \end{matrix}\right.\, \, \, \, \, \, \, \, \, \, \, \, (2)$

将式（2）代入式（1）得：

$\vec{r}=\begin{bmatrix} 1 & 0 & 0\\ 0 & \cos \gamma & \sin \gamma \\ 0 & -\sin \gamma& \cos \gamma \end{bmatrix}\begin{bmatrix} x_{0}\vec{e}_{x}^{'}\\ r\cos \alpha \vec{e}_{y}^{'}\\ r\sin \alpha \vec{e}_{z}^{'}\end{bmatrix}$

定义坐标轴绕x轴旋转 $\gamma$ 角度的旋转矩阵为：

$R_{xcoor}\left ( \gamma \right )=\begin{bmatrix} 1 & 0 & 0\\ 0 & \cos \gamma & \sin \gamma \\ 0 & -\sin \gamma& \cos \gamma \end{bmatrix}$

由此可以通过坐标旋转矩阵 $R_{xcoor}\left ( \gamma \right )$ 与位置矢量在原坐标下的坐标相乘，由此得到位置矢量在旋转后坐标系中的坐标。

2.2 坐标系绕y轴旋转

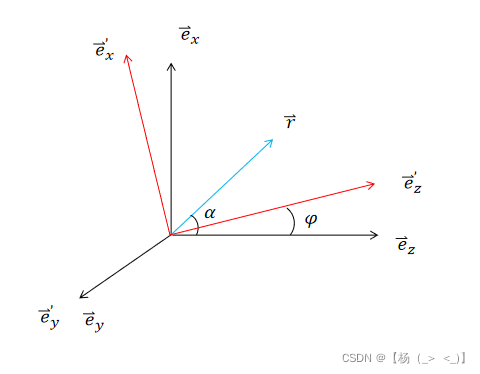
位置矢量在原坐标系下的表达式：

$\vec{r}=r\sin \alpha \vec{e_{x}}+y_{0}\vec{e_{y}}+r\cos \alpha \vec{e_{z}}\, \, \, \, \, \, \, \, (3)$

原坐标轴在旋转后的坐标轴上的表达式：

$\left\{\begin{matrix} \vec{e}_{x}=\sin \varphi \vec{e}_{z}^{'}+\cos \varphi \vec{e}_{x}^{'} \\ \vec{e}_{y}=\vec{e}_{y}^{'}\\ \vec{e}_{z}=\cos \varphi \vec{e}_{z}^{'}-\sin \varphi \vec{e}_{x}^{'} \end{matrix}\right.\, \, \, \, \, \, \, \, \, \, \, \, (4)$

将式（4）代入式（3）得：

$\vec{r}=\begin{bmatrix} \cos \varphi & 0 &-\sin \varphi \\ 0& 1 &0 \\ \sin \varphi &0 &\cos \varphi \end{bmatrix}\begin{bmatrix} r\sin \alpha\vec{e}_{x}^{'}\\y_{0} \vec{e}_{y}^{'}\\ r\cos \alpha\vec{e}_{z}^{'}\end{bmatrix}$

定义坐标轴绕x轴旋转 $\gamma$ 角度的旋转矩阵为：

$R_{ycoor}\left ( \varphi \right )=\begin{bmatrix} \cos \varphi & 0 &-\sin \varphi \\ 0& 1 &0 \\ \sin \varphi &0 &\cos \varphi \end{bmatrix}$

由此可以通过坐标旋转矩阵 $R_{ycoor}\left ( \varphi \right )$ 与位置矢量在原坐标下的坐标相乘，由此得到位置矢量在旋转后坐标系中的坐标。

2.3 坐标系绕z轴旋转

位置矢量在原坐标系下的表达式：

$\vec{r}= r\cos \alpha \vec{e_{x}}+ r\sin \alpha\vec{e_{y}}+ z_{0}\vec{e_{z}}\, \, \, \, \, \, \, \, (5)$

原坐标轴在旋转后的坐标轴上的表达式：

$\left\{\begin{matrix} \vec{e}_{x}=\cos \theta\vec{e}_{x}^{'}-\sin \theta \vec{e}_{y}^{'} \\ \vec{e}_{y}=\sin \theta \vec{e}_{x}^{'}+\cos \theta \vec{e}_{y}^{'} \\ \vec{e}_{z}=\vec{e}_{z}^{'}\\ \end{matrix}\right.\, \, \, \, \, \, \, \, \, \, \, \, (6)$

将式（6）代入式（5）得：

$\vec{r}=\begin{bmatrix} \cos \theta & \sin \theta &0\\ -\sin \theta & \cos \theta &0 \\ 0 &0 &1 \end{bmatrix}\begin{bmatrix} r\cos \theta \vec{e}_{x}^{'}\\r\sin \theta \vec{e}_{y}^{'}\\z_{0} \vec{e}_{z}^{'}\end{bmatrix}$

定义坐标轴绕x轴旋转 $\gamma$ 角度的旋转矩阵为：

$R_{zcoor}\left ( \theta \right )=\begin{bmatrix} \cos \theta & \sin \theta &0\\ -\sin \theta & \cos \theta &0 \\ 0 &0 &1 \end{bmatrix}$

由此可以通过坐标旋转矩阵 $R_{zcoor}\left ( \theta \right )$ 与位置矢量在原坐标下的坐标相乘，由此得到位置矢量在旋转后坐标系中的坐标。

不难发现：

$R_{xcoor}\left ( \gamma \right )=R_{x}\left ( -\gamma \right )$ $R_{ycoor}\left ( \varphi \right )=R_{y}\left ( -\varphi \right )$ $R_{zcoor}\left ( \theta \right )=R_{z}\left (- \theta \right )$

由此，我们可以认为坐标系绕轴旋转后的位置矢量坐标值等于位置矢量绕该轴反方向旋转相同角度后的坐标值。

三、卫星轨迹建立

3.1 轨道六根数

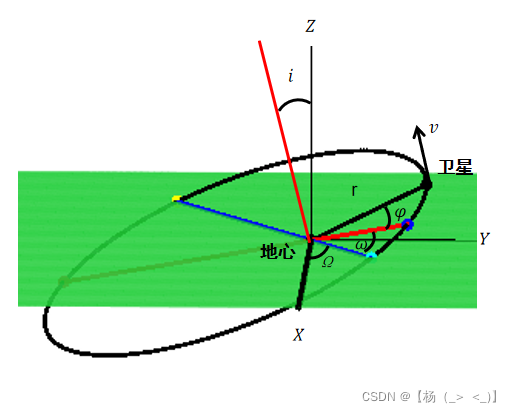
图1

在航天中，除了用速度，位置（均为三维矢量）描述卫星的轨迹，还可以用轨道六根数描述。轨道六根数：

半长轴 $a$ ：近地点与远地点距离的一般。
离心率 $e$ ：和半长轴共同确定轨道形状和尺寸。
轨道倾角 $i$ ：轨道面与赤道面的夹角。
升交点赤经 $\Omega$ ：轨道面与赤道面交线所在经度，和轨道倾角共同确定轨道面位置。
近心点辐角 $\omega$ ：近心点连线与轨赤交线的夹角，确定轨道在轨道面的指向。
真近点角 $\varphi$ ：卫星位置与近地点间的夹角，确定卫星在轨道的位置。

椭圆轨道和双曲线轨道需要六个根数才能确定轨迹；抛物线轨道由于离心率固定为1，所以只需五个根数就能确定抛物线轨道；圆轨道离心率固定为0，且各向同性，不存在指向问题，所以只需四个根数即可。

3.2 卫星轨迹构建

对图1轨道绕z轴顺时针旋转 $\Omega$ ，新的轨道与赤道的交线位于x轴上；对新的轨道绕x轴顺时针旋转 $i$ ，此时轨道在赤道面上。在赤道面的轨迹分析根据《SAR笔记-卫星轨道建模》可以得到，由此卫星的三维轨迹可以由《SAR笔记-卫星轨道建模》中的二维轨迹先x轴逆时针旋转 $i$ ，再绕z轴逆时针旋转 $\Omega$ 得到。

上述分析的是ECI坐标系的卫星轨迹，为了获得ECR坐标系下的卫星轨迹，根据坐标系旋转与位置矢量旋转只是旋转方向不同的关系，只需将卫星轨迹绕z轴顺时针（迎着z轴看）旋转 $w_{e}t$ 角度， $w_{e}$ 为地球自转角速度。

3.3 仿真结果

ECI坐标系下卫星运行轨迹：

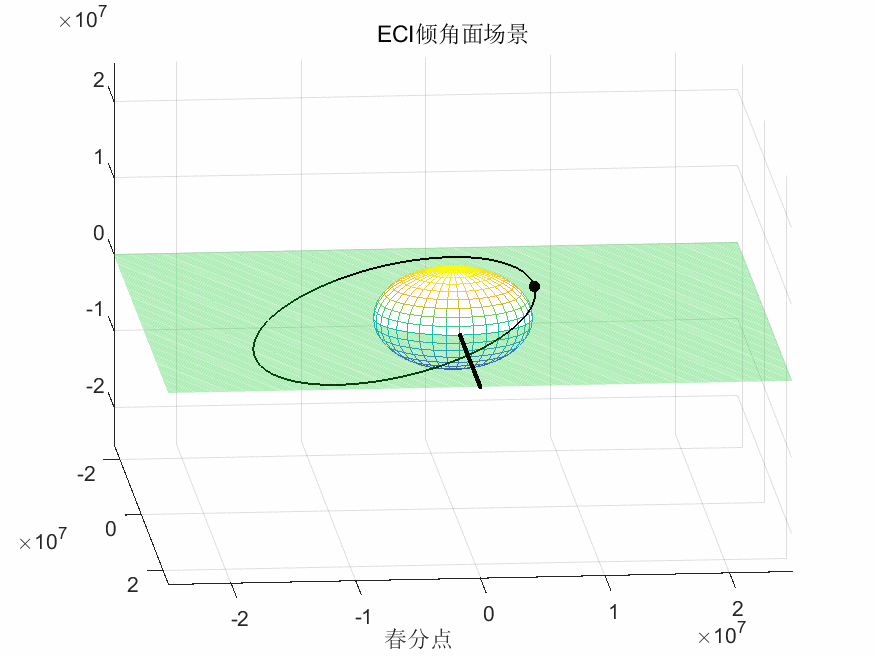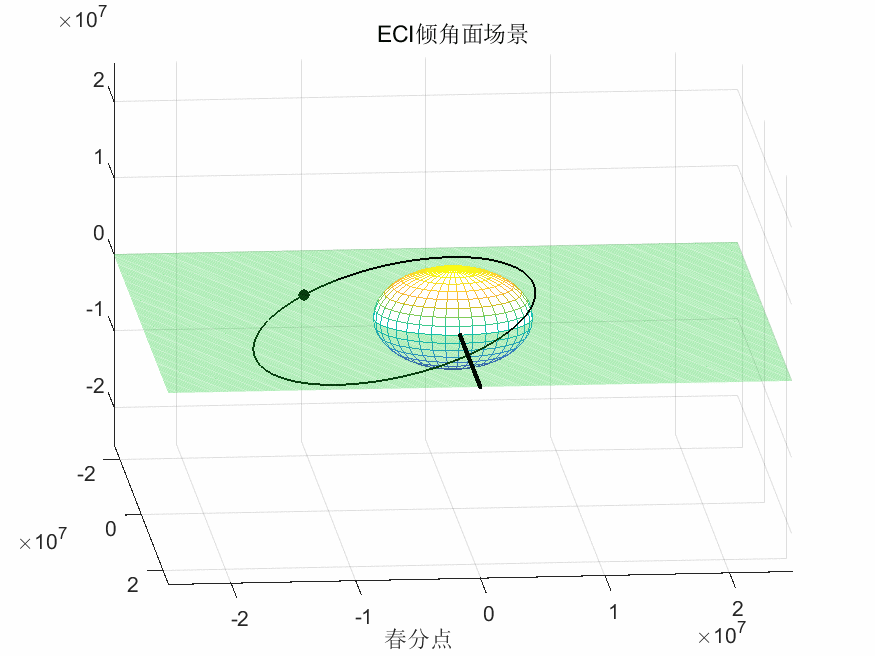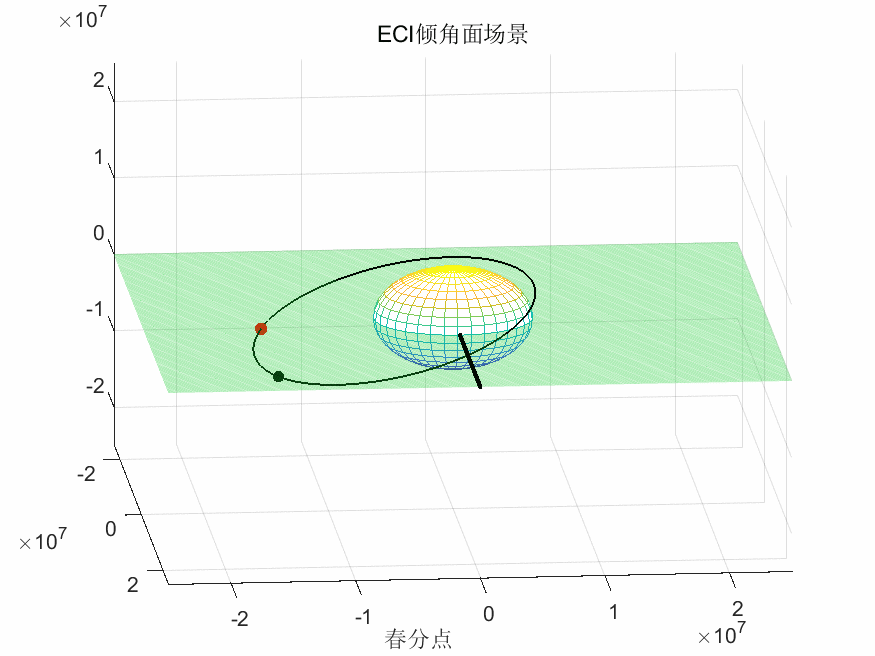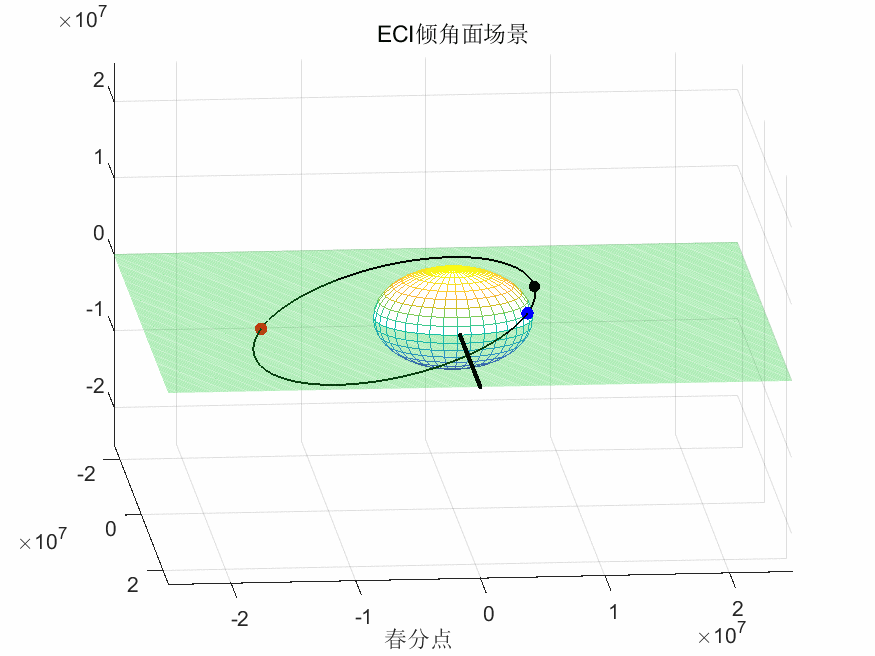
ECR坐标系下卫星运行轨迹：

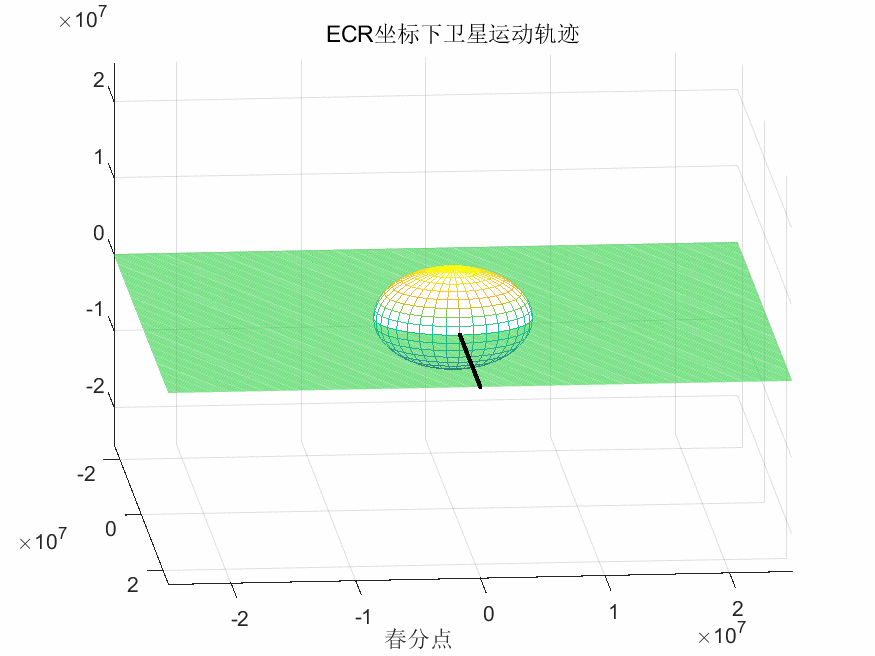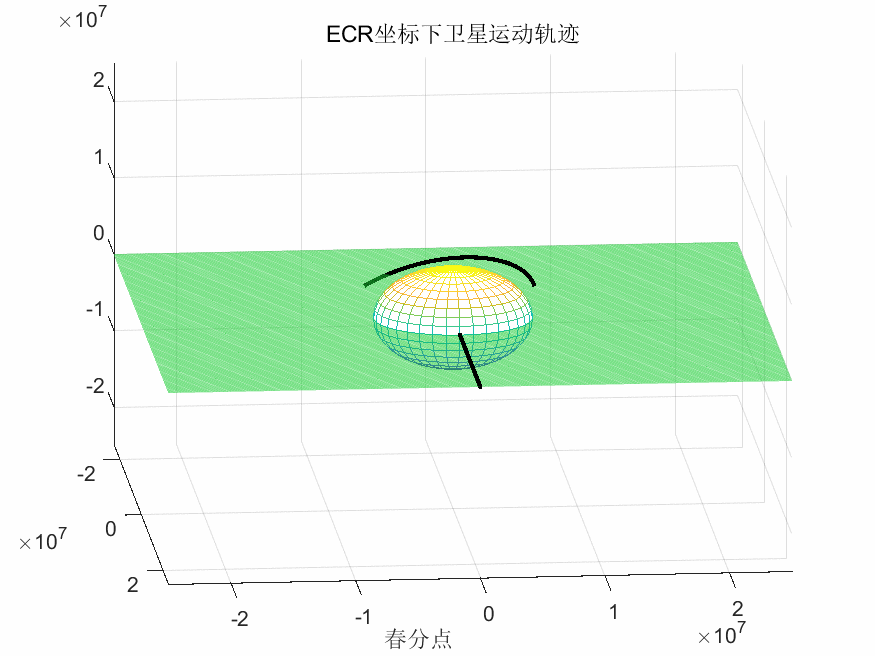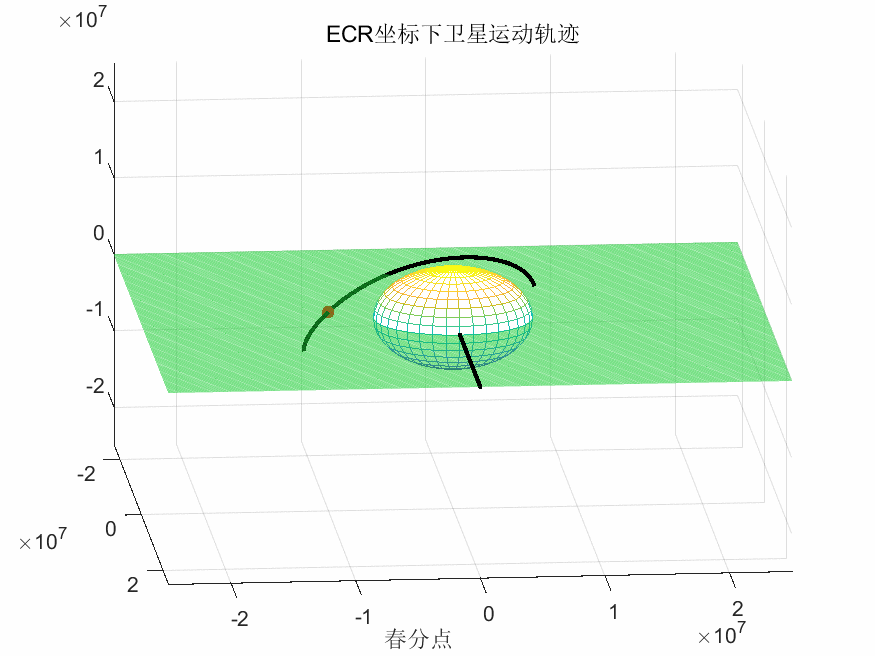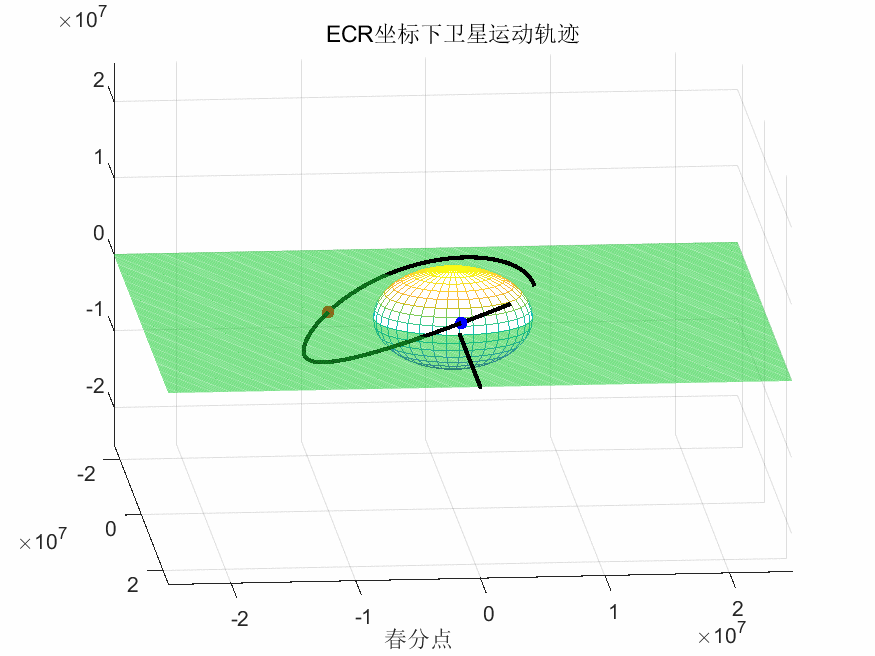
ECR坐标系下星下点轨迹

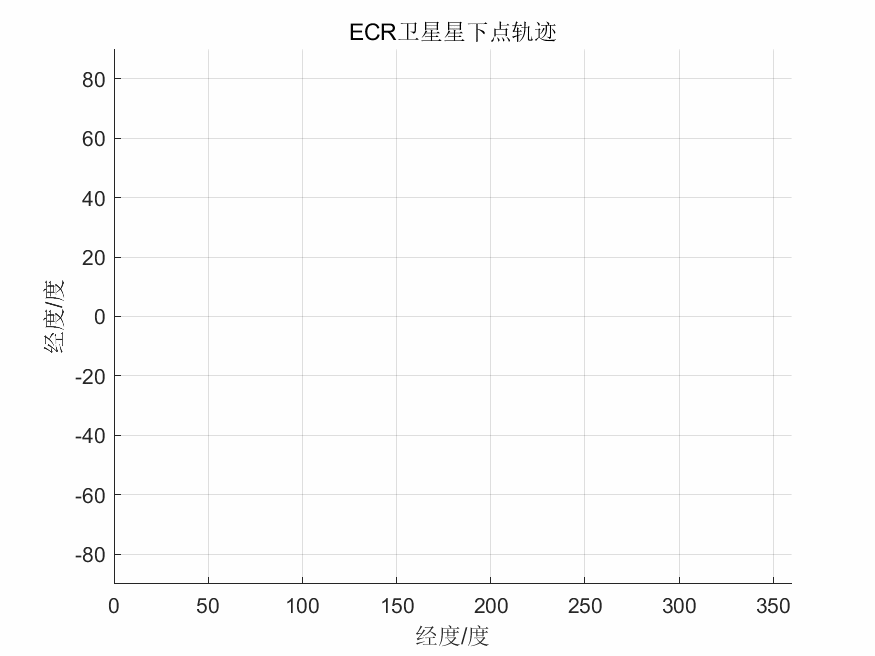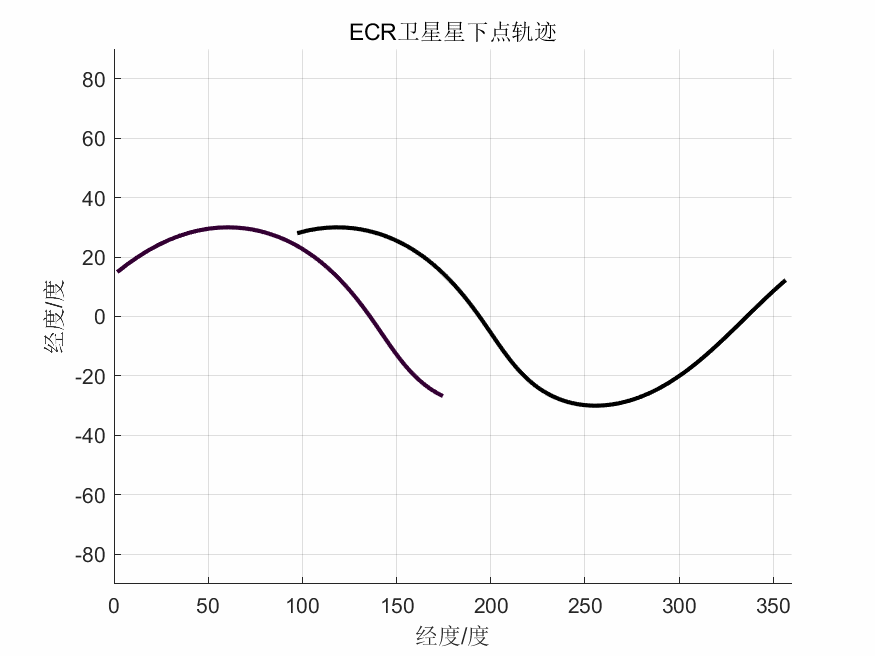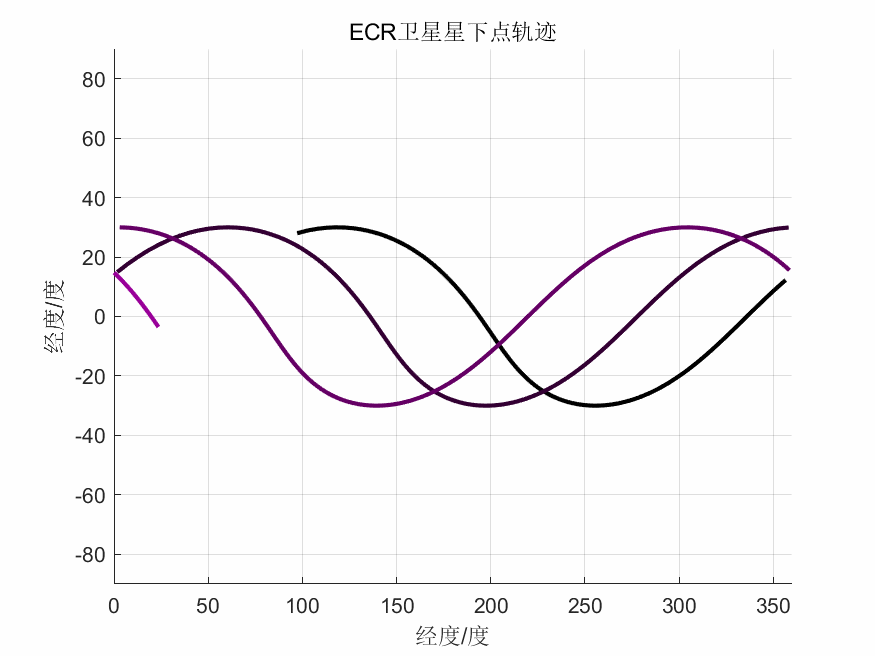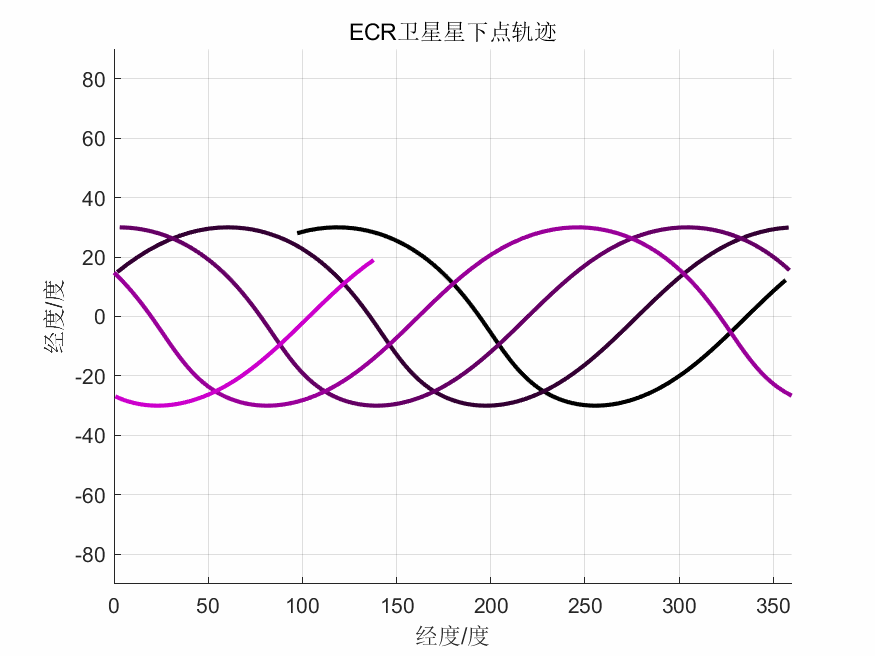
代码见：卫星轨道三维动态图

总结

本节主要根据轨道六根数生成对应的卫星轨迹三维动态图，主要由位置矢量旋转以及坐标系旋转关系得到。卫星轨道分析在雷达和通信领域都有重要作用，尤其是SAR领域，卫星轨迹对于SAR成像质量影响很大。

SAR笔记-卫星轨迹（三维建模）

SAR系列文章目录

前言

一、位置矢量旋转

1.1 位置矢量绕x轴旋转

1.2 位置矢量绕y轴旋转

1.3 位置矢量绕z轴旋转

二、坐标系旋转

2.1 坐标系绕x轴旋转

2.2 坐标系绕y轴旋转

2.3 坐标系绕z轴旋转

三、卫星轨迹建立

3.1 轨道六根数

3.2 卫星轨迹构建

3.3 仿真结果

总结

公告

标签

SAR笔记-卫星轨迹（三维建模）

SAR系列文章目录

前言

一、位置矢量旋转

1.1 位置矢量绕x轴旋转

1.2 位置矢量绕y轴旋转

1.3 位置矢量绕z轴旋转

二、坐标系旋转

2.1 坐标系绕x轴旋转

2.2 坐标系绕y轴旋转

2.3 坐标系绕z轴旋转

三、卫星轨迹建立

3.1 轨道六根数

3.2 卫星轨迹构建

3.3 仿真结果

总结

相关问题

公告

标签