【算法基础】图论之DFS&BFS&拓扑排序 万字总结 (16张图解+详细注释)
传送门⏬⏬⏬
- 一、如何理解“图”?
-
- 1、无向图
- 2、有向图
- 3、带权图(weighted graph)
- 4、小总结
- 二、图的存储方式
-
- 1、邻接矩阵存储方法
- 2、邻接表存储方法
- 3、对比总结
- 三、总结DFS和BFS
- 四、实战题目
-
- 1、DFS遍历图的模板
- 2、Acwing.846. 树的重心 [DFS搜索树]
-
- 题目
- 思路
- 代码
- 3、Acwing847. 图中点的层次 [BFS]
-
- 题目
- 思路
- 代码
- 4、拓扑排序
-
- 知识点
- 题目描述
- 思路
- AC代码
- 四、结尾
前言
你好啊,既然你点进来了,那就进来学点知识??蓝桥杯将至,来学点常考算法吧,不多bb开🚀
另外,欢迎关注我的专栏,用心写题解
一、如何理解“图”?
图
Graph是一种非线性表数据结构,和树比起来,这是一种更加复杂的非线性表结构。我们知道,树中的元素我们称为节点,图中的元素我们就叫作顶点(vertex)。从我画的图中可以看出来,图中的一个顶点可以与任意其他顶点建立连接关系。我们把这种建立的关系叫作边(edge),另外,树是一种特殊的图, 是无环的, 并且连同。
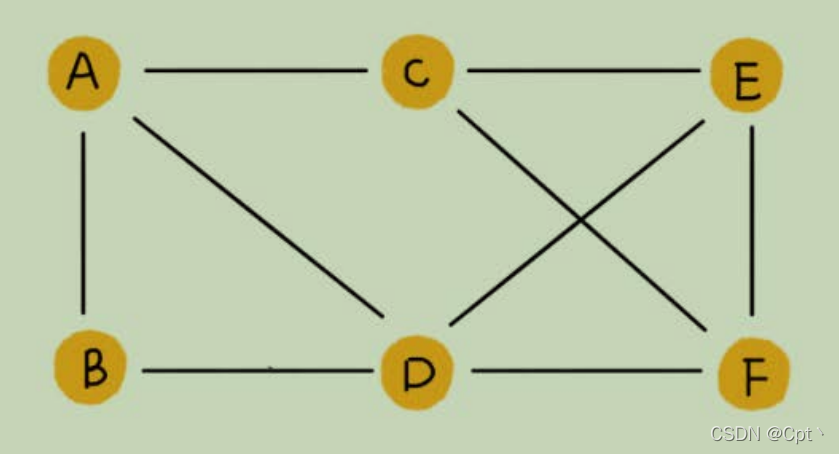
1、无向图
- 边是没有方向的
a——b相当于 可以a->b b->a,所以无向图是一种特殊的有向图(有向图开俩边就是无向图)。 - 比如,社交网络,就是一个非常典型的图结构。我们就拿微信举例子吧。我们可以把每个用户看作一个
顶点。如果两个用户之间互加好友,那就在两者之间建立一条边。所以,整个微信的好友关系就可以用一图的表示:如何存储微博、微信等社交网络中的好友关系?张图来表示。其中,每个用户有多少个好友,对应到图中,就叫作顶点的度(degree),就是跟顶点相连接的边的条数。
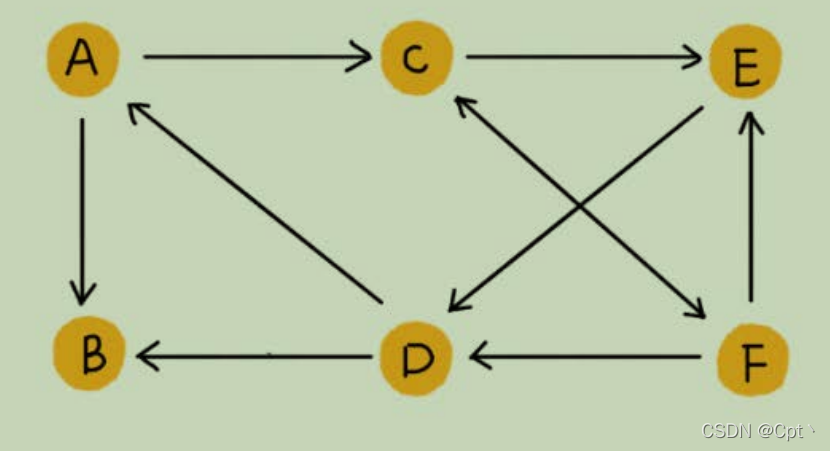
2、有向图
- 边是有方向的
A—>B是加上了方向性 (学这个就行)。 - 以微博举例,微博允许单向关注,也就是说,用户A关注了用户B,但用户B可以不关注用户A。那我们如何用图来表示这种单向的社交关系呢?我们可以把刚刚讲的图结构稍微改造一下,引入边的“方向”的概念。如果用户A关注了用户B,我们就在图中画一条从A到B的带箭头的边,来表示边的方向。如果用户A和用户B互相关注了,那我们就画一条从A指向B的边,再画一条从B指向A的边。我们把这种边有方向的图叫作“
有向图”。
3、带权图(weighted graph)
- 在带权图中,每条边都有一个权重(
weight),我们可以通过这个权重来表示QQ好友间的亲密度。
4、小总结
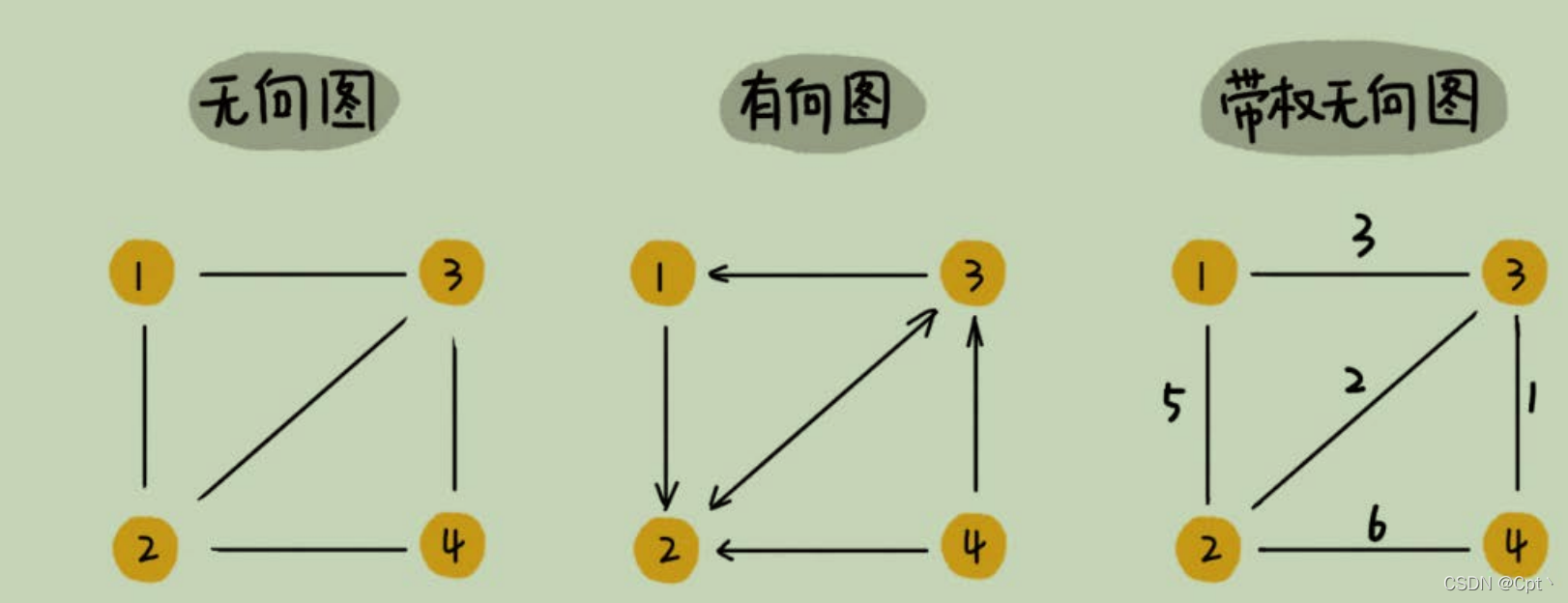
关于图的概念比较多,我今天也只是介绍了几个常用的,理解起来都不复杂,不知道你都掌握了没有?掌握了图的概念之后,我们再来看下,如何在内存中存储图这种数据结构呢?
二、图的存储方式
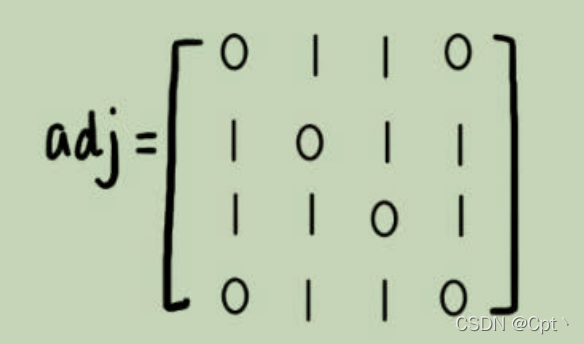
1、邻接矩阵存储方法
g[x][y](二维数组) 空间复杂度 n2 适合稠密图。
缺点:只能保留一条最短的边,如果我们存储的是稀疏图(Sparse Matrix),也就是说,顶点很多,但每个顶点的边并不多,那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户,对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多,一般也就三五百个而已。如果我们用邻接矩阵来存储,那绝大部分的存储空间都被浪费了。
2、邻接表存储方法
用的比较多,相当于n个单链表,与哈希的拉链法相似,每一个结点开了一个单链表 ,存储可以到的距离为一的点。图中画的是一个有向图的邻接表存储方式,每个顶点对应的链表里面,存储的是指向的顶点。对于无向图来说,只需要再反方向加一条边即可。eg.第一个单链表存储的是 和h[1] 可以到的距离为1的点
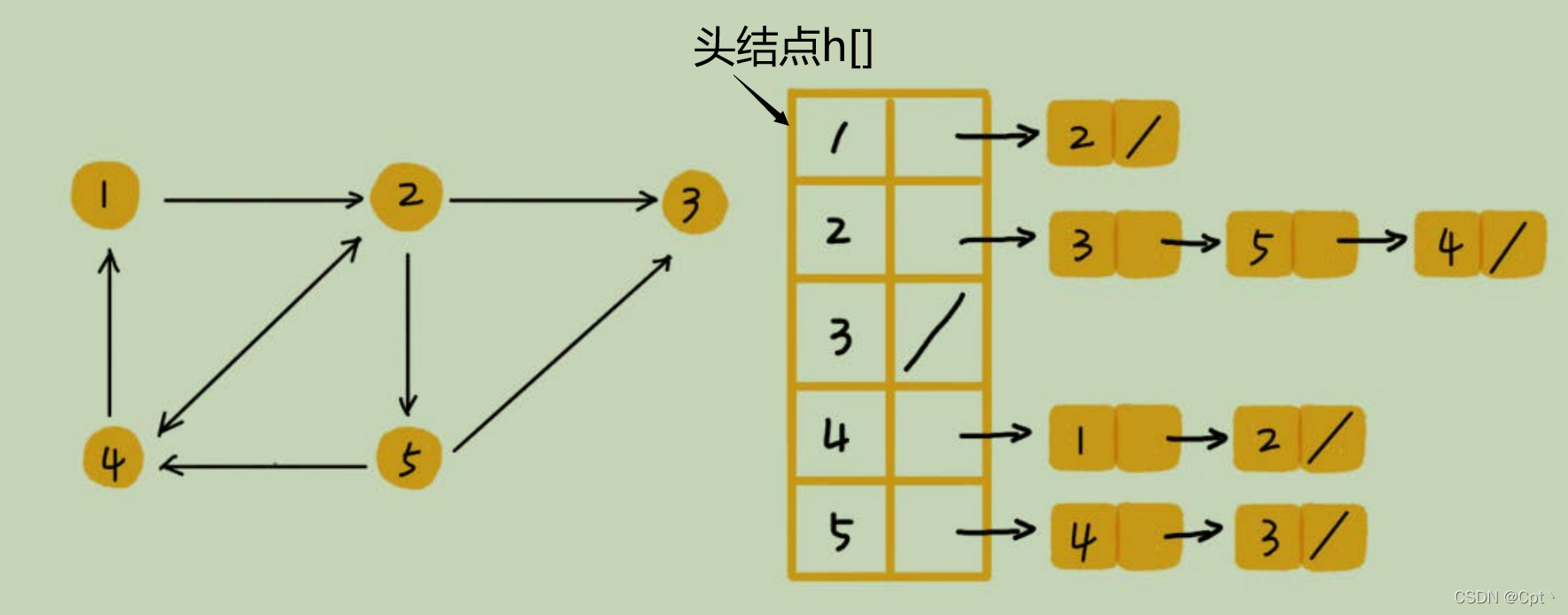
3、对比总结
| 邻接矩阵 | 邻接表 | |
|---|---|---|
| 优点 | 存储方式简单、直接 、方便计算。 | 邻接表存储起来比较节省空间 |
| 缺点 | 比较浪费存储空间 | 使用起来就比较耗时间(查询麻烦) |
三、总结DFS和BFS
| DFS | BFS | |
|---|---|---|
| 数据结构 | O(n) |
O(2n) 这里的 n:深度 |
| 时间复杂度 | stack栈 |
queue队列 |
| 区别 | 不具备最短性 | 最短路 |
先上图

-
DFS[暴搜]:从头走到尾,如果没找到,就一层一层地返回重新找另一个子链,然后再继续深入找,左边找完找右边。
-
我的另一篇暴搜文章(建议收藏) DFS “深搜”排列数字+八皇后问题 ( 图解+详细注释 )

-
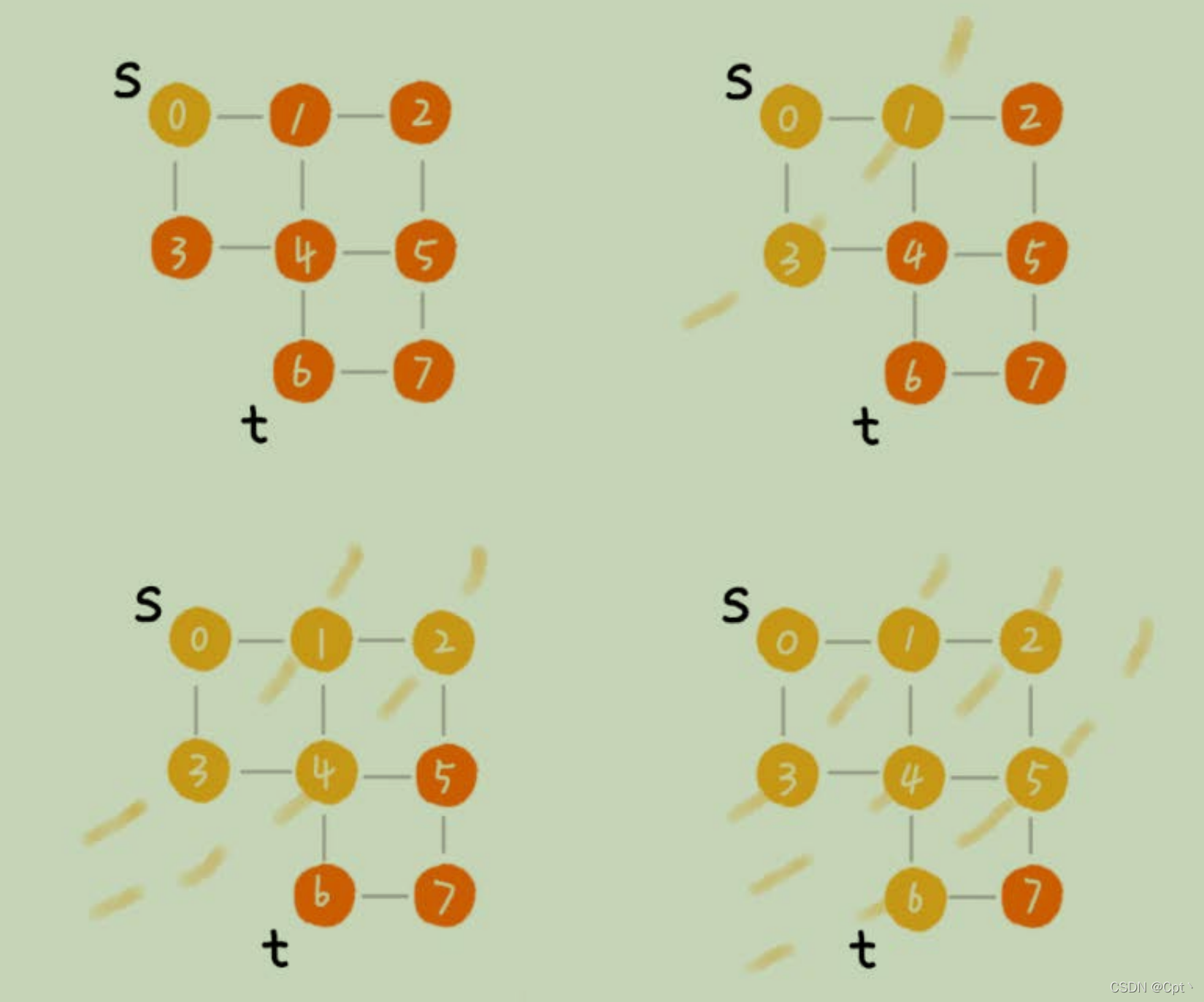
BFS:它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。
我的另一篇文章BFS 走迷宫 八数码
四、实战题目
1、DFS遍历图的模板
- 这是为数不多DFS的模板
图的边怎么构建?本质就是单链表的插入 。不懂可以看我这篇文章 文章链接 点击跳转
e[idx] = x, ne[idx] = ne[k], ne[k] = idx++;首先是赋值,然后改变指针方向,再让原来的元素直线自己,最后移动下标继续进行操作 最重要的是ne[idx] = ne[k],ne[k] = idx这俩步的操作 次序一定不能颠倒 下面是我画的图方便理解

图解遍历路径 ↓

- 可以发现是一层一层搜索
算法模板↓
#include #include #include using namespace std;const int N = 100010, M = N * 2;int n, m;int h[N], e[M], ne[M], idx;bool st[N]; //标记每个走过的点,防止二次遍历//构建边void add (int a, int b) { e[idx] = b, h[idx] = ne[a], h[a] = idx++;}//暴搜 核心模板void dfs (int u) { st[u] = true; for (int i = h[u]; i != -1; i = ne[i]) {//遍历每个根节点 int j = e[i]; if (!st[j]) { dfs(j); } }}int main () { memset(h, -1, sizeof h);//初始化每个点为空[含义:没有来过] dfs(1); return 0;}2、Acwing.846. 树的重心 [DFS搜索树]
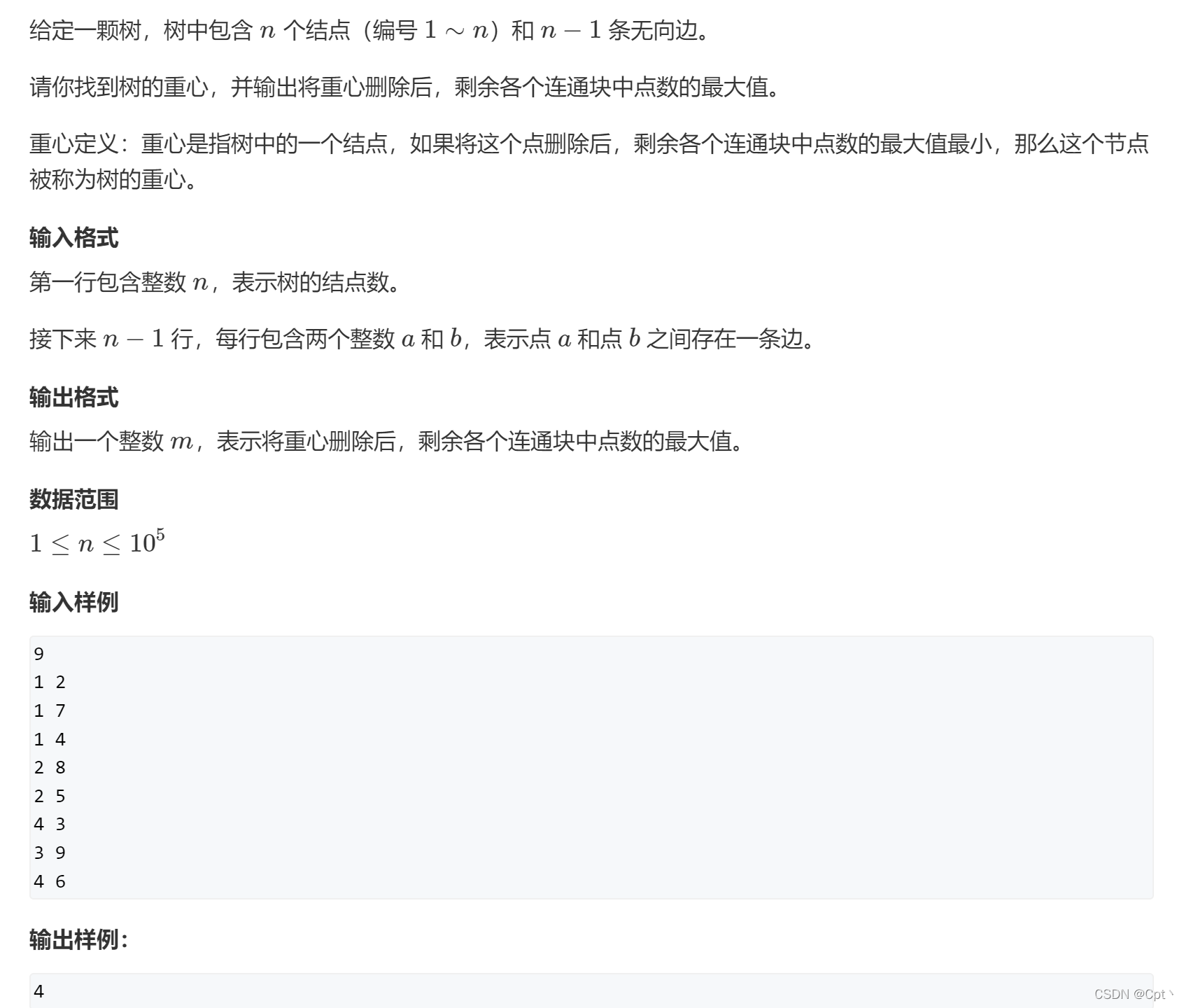
题目
思路
- 树的重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
题目解读:结合下图一起看,图中画的是输入样例的树,也可以理解为一个具有无向边且没有环结构的图。就是删除每个节点,然后记录每个节点的连通块的最大值MAX。然后遍历比较每个节点,更新每个节点的连通块的最大值MAX的MIN ,建议断句理解. 比如下图俩个例子 第一个删除节点2后,最大连通块为6 ,此时res2=6 ,ans=(ans=N,res2)=6 。第二个删除节点4后,此时res4=5记录当前,ans=min(ans=6,res4)=5



代码
#include #include #include using namespace std;const int N = 100010, M = N * 2;//无向图,所以每个节点至多对应2n-2条边int h[N]; //队头int e[M]; //存储元素的值int ne[M]; //存储列表的next值 int idx; //单链表指针int n,m; int ans = N; //保存答案 N为题目范围 MAXbool st[N]; //记录节点是否被访问过,用于遍历每个点//图结点的边 [原理和单链表的插入一样] void add (int a,int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx++;}//以u为跟的子树中点的数量[包括u节点]int dfs (int u) { st[u] = true; //标记一下[表示已经搜过] 保证每个点只遍历一次 int sum = 1;//存储以u为根的树的节点数(包括u )如图中的4号节点 int res = 0;//存储 删掉某个节点之后,最大的连通子图节点数 for (int i = h[u]; i != -1;i = ne[i]) {//遍历每个点 int j = e[i]; if (!st[j]) { int s = dfs(j);// u节点的单棵子树节点数 如图中size值 res = max(res, s);// 保存最大联通子图的节点数 sum += s;//以j为根的树 的节点数 } } res = max(res, n - sum);// 选择u节点为重心,最大的 连通子图节点数 ans = min(ans, res);//最小的最大联通子图的节点数 return sum; }int main () { cin >> n >> m; memset(h, -1, sizeof h); // 所有点赋值为空[-1] // 树中是不存在环的,对于有n个节点的树,必定是n-1条边 for (int i = 0; i < n - 1; i ++) { int a, b; cin >> a >> b; add(a, b), add(b, a); //构造无向边 } dfs(1); //哪个点开始搜都行 因为每个点都要遍历 cout << ans << endl; return 0;}3、Acwing847. 图中点的层次 [BFS]
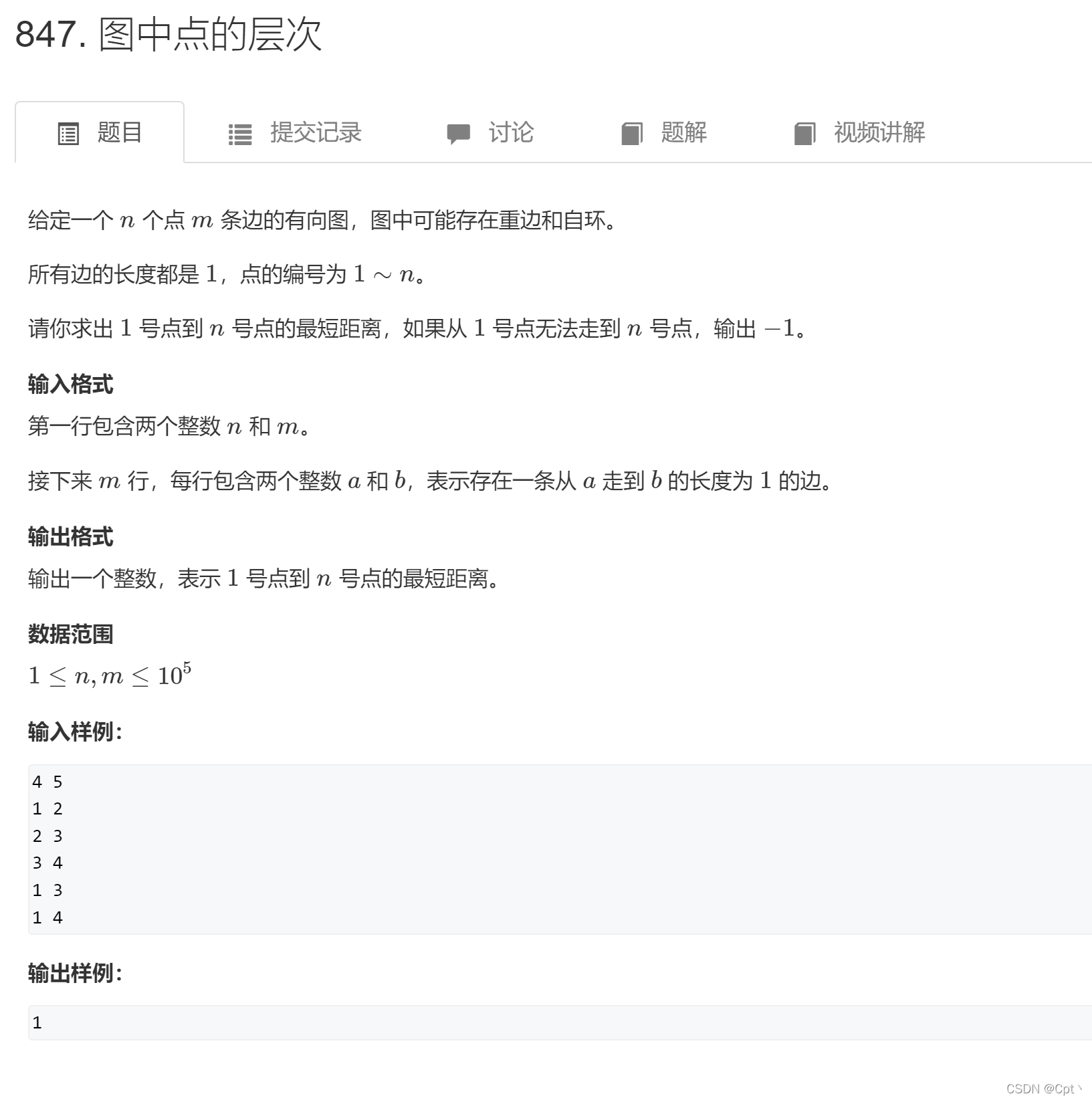
题目
图中 所有边都是1 由此可以BFS来做
重边 :俩条边指向一个结点
自环 : 结点自己指向自己
思路

核心
for (int i = h[t]; i != -1; i = ne[i]) // ne[i]上的点都是与i节点距离为1的点 { int j = e[i]; // 点的值 if (d[j] == -1) // 如果j没有被遍历过 { d[j] = d[t] + 1; // 因为路径长度都是1,上一个点的长度加上1即可 q.push(j); // 将j加到队列中 } }代码
不懂参考文章
#include #include #include #include #include using namespace std;const int N = 100010;int n, m;int h[N], e[N], ne[N], idx;int d[N], q[N];//构建边void add (int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx ++;}int bfs (int n) { memset(d, -1, sizeof d); queue<int> q; d[1] = 0; q.push(1); //加入起点 while (!q.empty()) { int t = q.front(); // t 保存队头 q.pop(); //弹出队头元素 for (int i = h[t]; i != -1; i = ne[i]) // ne[i]上的点都是与i节点距离为1的点 { int j = e[i]; // e[i]保存下标 if (d[j] == -1) // 如果j没有被遍历过 { d[j] = d[t] + 1; // 因为路径长度都是1,所以直接在上一步的基础上加上1即可 q.push(j); // 将j加到队列中 } } } return d[n]; // 返回的d[n]即是节点1到节点n的距离}int main () { cin >> n >> m; memset(h, -1, sizeof h); for (int i = 0; i < m; i ++ ) { int a, b; scanf("%d%d", &a, &b); add(a, b); } cout << bfs(n) << endl; return 0;}4、拓扑排序
知识点
拓扑排序知识点:拓扑排序本身就是基于有向无环图的一个算法,同时,有向无环图也被称为拓扑图。有向性上面说了。环是什么?像a->b->c->a这样,就是环,图中一旦出现环,拓扑排序就无法工作了。出度 一个点指向其他点的边的数量。
入度 一个点被指向的边的数量。
拓扑序列:只有从前指向后面的边,没有从后面指向前面的边,如图:
下面这种就不是拓扑序列 ↓
- 结论:只有带环的才有指向后面的边,由此有向无环图也被称为拓扑图。
题目描述
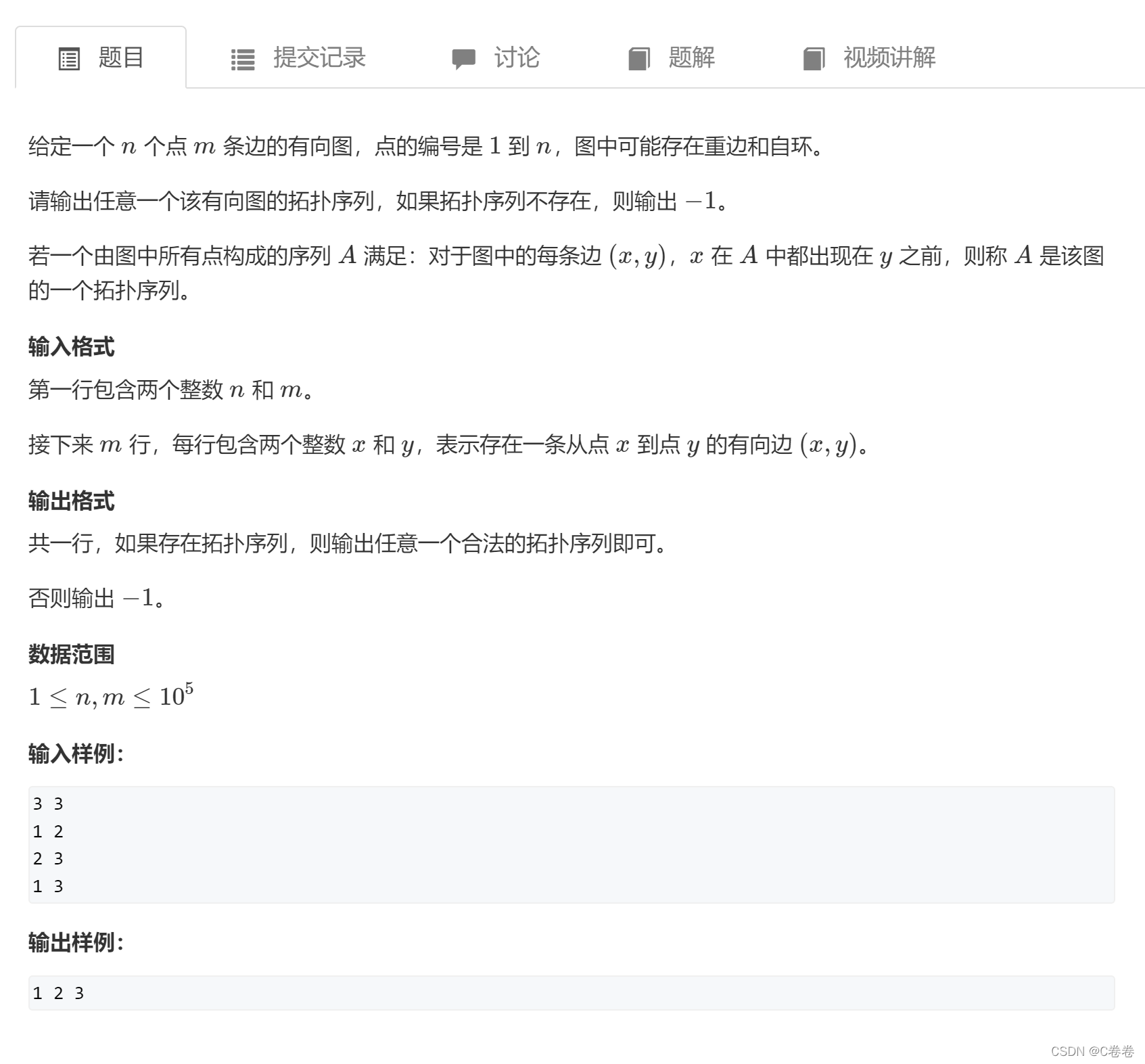
思路
遍历寻找到起点,然后删去该点,最后遍历点所有出边。
AC代码
#include #include #include #include using namespace std;const int N = 100010;int e[N], ne[N], h[N], idx, n, m;int d[N]; //存储每个元素的入度int top[N];//拓扑排列的序列int cnt = 1; //记录拓扑元素的个数//邻接链表存储void add (int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx++;}//判断是否符合拓扑序列bool topsort() { queue<int> q; int t; for (int i = 1; i <=n; i ++) { if(d[i] == 0){//遍历寻找起点[入度为0的点] q.push(i); } } while (!q.empty()) { t = q.front();//每次取出队列的首部 top[cnt ++] = t;//加入到 拓扑序列中 q.pop();//删除这个点 for (int i = h[t]; i != -1;i = ne[i]) { int j = e[i]; d[j]--; // j的入度-1 if (d[j] == 0 ) {//如果j入度为0,加入队列当中 q.push(j); } } } //当所以点都入队,cnt ==n if (cnt < n) { return 0; } else { return 1; }}int main () { int a, b; cin >> n >> m; memset(h, -1, sizeof h); while (m --) { cin >> a >> b; add(a, b); d[b]++;//a——>b ,b的入度+1 } if (topsort() == 0) { cout << "-1"; } else { for (int i = 1; i <= n; ++ i) { cout << top[i] << " "; } } return 0;}四、结尾
感谢你能看完, 如有错误欢迎评论指正,这篇文章创作用时
5小时,字数1w,如果对你有帮助的话,点个赞鼓励下, 谢啦!!☆⌒(*^-゜)v







