九日集训day3【刷题】【九日集训】

前言

今天是九日集训第三天，学校事情有点多，加上晚上还有蓝桥杯的每日打卡，搞到9点多才开始看英雄哥的九日集训，只能先把必做题写了，剩下的题有时间再写。
这两天都有在看英雄哥的直播，昨天5点起来，今天睡过头哈哈，6点才起。挺兴奋的，就是中午必须得睡久点，不然太困扛不住。

33. 搜索旋转排序数组

暴力遍历：

class Solution {public:    int search(vector<int>& nums, int target) { for(int i = 0; i < nums.size(); i++) {     if(nums[i] == target)  return i; } return -1;    }};

二分：

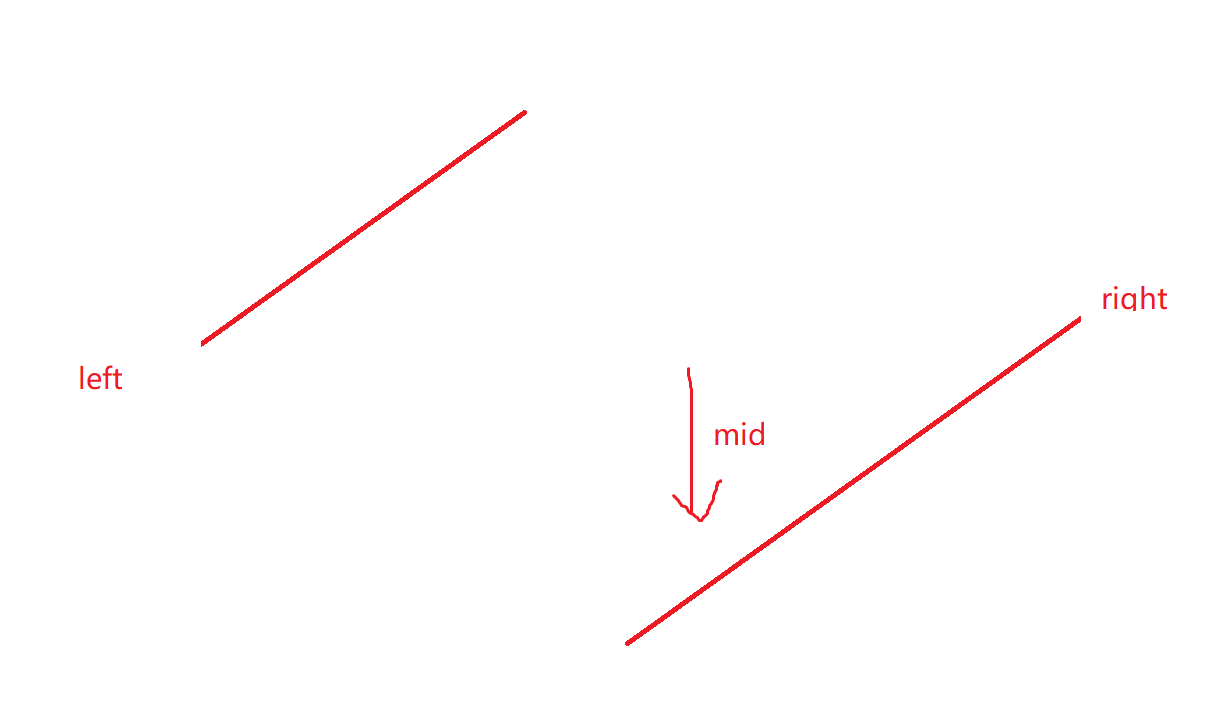
数组本身不是有序的，进行旋转后只保证了数组的局部是有序的，将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。
0 1 2 4 5 6 7在下标3处经旋转变为4 5 6 7 0 1 2

中间坐标为3，指向的4是，先用第一个值和mid的值比较一下，如果左端点小于中间值，说明【0，mid】是有序的。然后看target是否再有序的区间内，不在就就搜索无序的那个区间

注意考虑数组如果没有元素或者只有一个元素的情况。

时间复杂度O(LogN) 空间复杂度O(1)

class Solution {public:    int search(vector<int>& nums, int target)     { int n = nums.size(); //考虑只有一个元素和没有元素的情况 if(n == 0)     return -1; if(n == 1) {     if(nums[0] == target)  return 0;     else  return -1; } int left = 0, right = n-1; while(left <= right) {     int mid = ((right-left)>>1)+left;//避免溢出     if(nums[mid] == target)  return mid;     //先判断哪个区间是有序区间     if(nums[0] <= nums[mid])//有序     {  if(target >= nums[0] && target < nums[mid])      //target在有序区间内，普通二分搜索即可      right = mid - 1;  else      //target在无序区间内      left = mid + 1;     }     else     {  //无序区间 进一步二分，也能分出一个有序和一个无序  if(target > nums[mid] && target <= nums[n-1])      left = mid + 1;  else      //target在有序区间      right = mid - 1;     } } return -1;//确实找不到    }};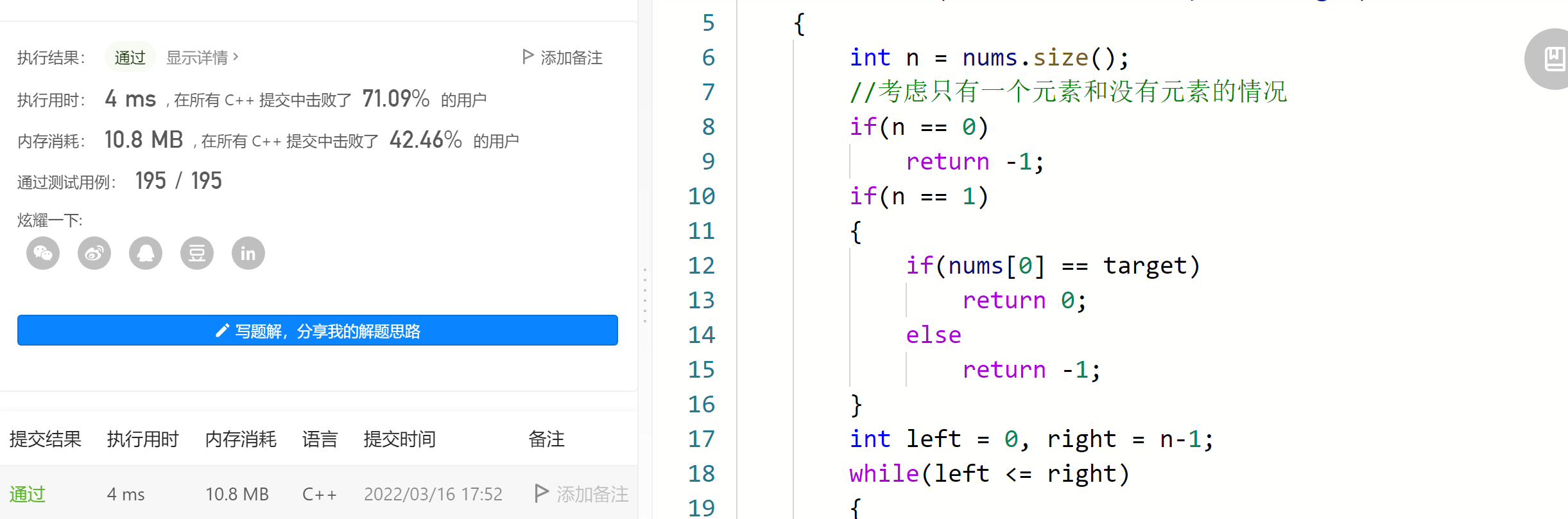

81. 搜索旋转排序数组 II

注意，此题与上题不同，如果数组存在相同的数据时，二分时无法辨别出有序区间

使用暴力解法即可

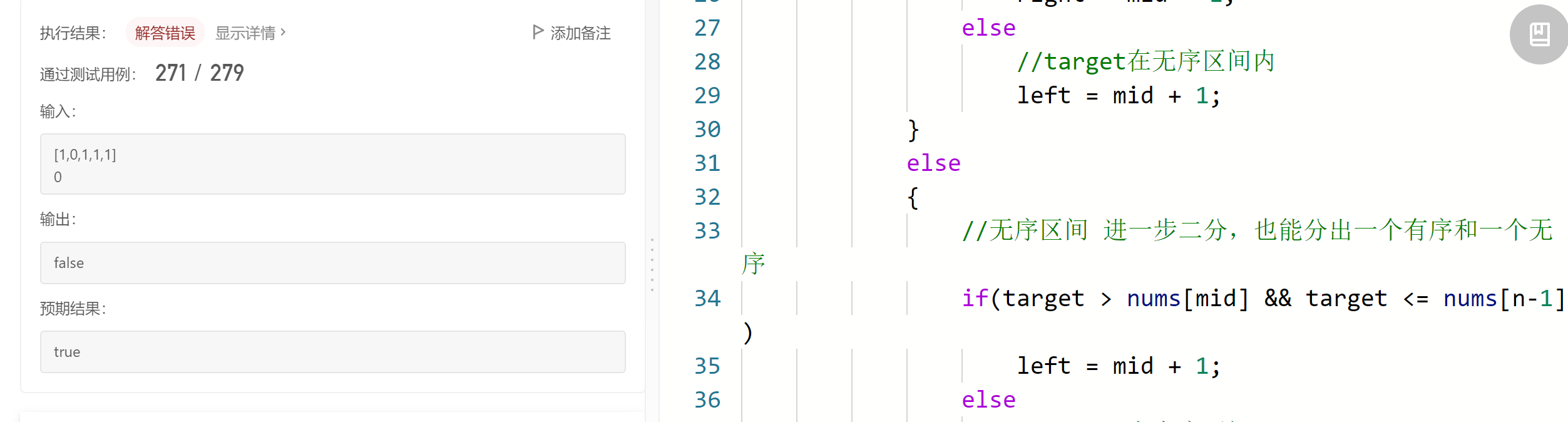
class Solution {public:    bool search(vector<int>& nums, int target) { for (int i = 0; i < nums.size(); i++)      if (nums[i] == target)  return true; return false;    }};

153. 寻找旋转排序数组中的最小值

暴力遍历：

定义一个min暴力遍历

class Solution {public:    int findMin(vector<int>& nums) { int n = nums.size(); int min = nums[0]; for(int i = 0; i < n; i++) {     if(nums[i] < min)  min = nums[i]; } return min;    }};

二分：

旋转后的数组无非就2种情况，第一种顺序不变，最小值就是最左边的值

第二种

用mid 与right比较，mid下标的值小于right时，说明mid是在最小值右边的，

mid下标的值大于right时，说明mid在最小值左边。

左闭右开的写法

class Solution {public:    int findMin(vector<int>& nums) { int left = 0, right = nums.size() - 1; //左闭右开的写法 while(left < right) {     int mid = (right - left)/2 + left;     //mid在最小值右边     if(nums[mid] < nums[right])  right = mid;//mid是访问不到的     //mid在最小值左边     else  left = mid + 1;//left是能访问到的，mid比较过的 } return nums[left];    }};

70. 爬楼梯

经典的斐波那契

用非递归的形式写比较好

class Solution {public:    int climbStairs(int n) { if(n <= 2)     return n; int a = 1, b = 2, temp; for(int i = 3; i <= n; i++) {     temp = a + b;     a = b;     b = temp; } return b;    }};

1137. 第 N 个泰波那契数

递归：

递归会超时

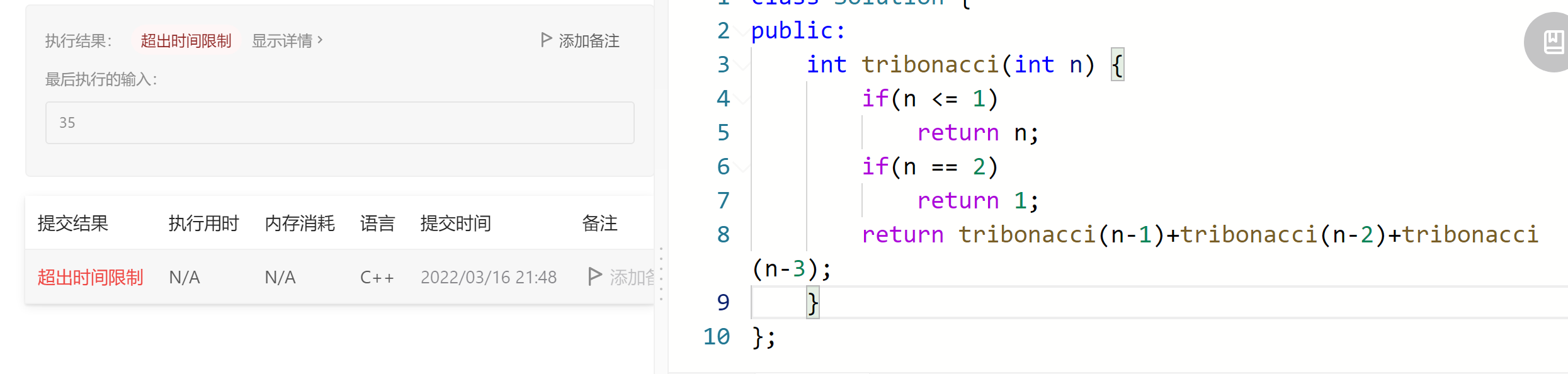
非递归：

class Solution {public:    int tribonacci(int n) { if(n == 0)     return 0; int t0 = 0, t1 = 1, t2 = 1; for(int i = 3; i <= n; i++) {     int tmp = t0 + t1 + t2;     t0 = t1;     t1 = t2;     t2 = tmp; } return t2;    }};