最近对问题

令P为笛卡儿平面上n>1个点构成的集合。简单起见，假设集合中的每个点都不一样。我们还假设这些点是按照其x轴坐标升序排列的。（如果不是这样，可以事先用类似合并排序这样的高效算法对其排序。)为了更加方便，我们还可以按照点的y轴坐标在另一个列表中进行升序排列，并将这个列表示为Q。
当2≤n≤3时，问题就可以通过蛮力算法求解。当n>3时，可以利用点集在x轴方向上的中位数m,在该处作一条垂线，将点集分成大小分别为$\lceil n/2\rceil 和\lfloor n/2\rfloor$的两个子集 P l 和 P r P_l和P_r Pl​和Pr​。即使得其中⌈n/2⌉个点位于线的左边或线上，⌊n/2⌋个点位于线的右边或线上。然后就可以通过递归求解子问题 P l 和 P r P_l和P_r Pl​和Pr​来得到最近点对问题的解。其中 d l 和 d r d_l和d_r dl​和dr​分别表示在 P l 和 P r P_l和P_r Pl​和Pr​中的最近对距离，并定义d=min{ d l , d r d_l,d_r dl​,dr​}。但请注意，d不一定是所有点对的最小距离，因为距离最近的两个点可能分别位于分界线的两侧。因此，在合并较小子问题的解时，需要检查是否存在这样的点。显然，我们可以只关注以分割带为对称的、宽度为2d的垂直带中的点，因为任何其他点对的距离都至少为d，如下图。

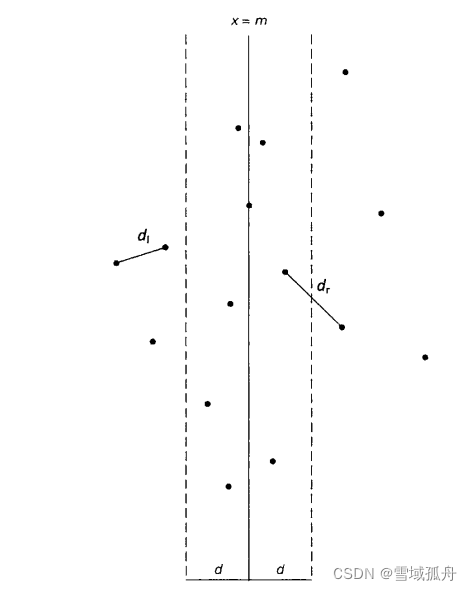
设S是来自Q,位于分割线2d宽度范围内的垂直带的点的列表。由于Q的特点，因此S是按照y轴坐标升序排列的。我们扫描该列表，当遇到更近的点对时，更新目前为止的最小距离 dmin d_{min} dmin​。初始情况下 dmin d_{min} dmin​=d,但接下来 dmin d_{min} dmin​≤d。设p(x,y)为列表中的点。如果另一个点p’(x’,y’)和p点的距离小于d，那么在列表S中，p’点一定位于p点后面，并且两点在y轴上的距离一定要小于d。在几何上，这也就意味着p’点一定包含在下图的矩形内。该算法的主要原理利用了以下事实：矩形内一般只能够包含少量候选点，因为在矩形每一边（左半边和右半边）内，点与点的距离至少为d。

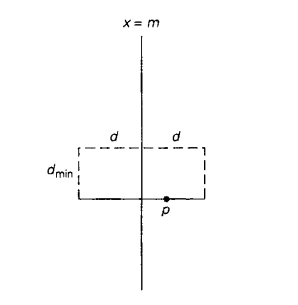
其实很容易证明，在矩形中满足条件的点（包括P在内）的总数不超过8个，更细致的研究表明这个数不会大于6。也就是说，在移动到下一个点之前，算法最多只需要考虑列表S中点p后面的5个点。

伪代码

EfficientClosePair(P,Q)//使用分治算法来求解最近对问题//输入：数组P中存储了平面n>=2个点，并且这些点按照x轴坐标升序排列//数组Q存储了与P相同的点，只是它是按照这点的y轴坐标升序排列//输出：最近点对之间的欧几里得距离if n <= 3返回由蛮力算法求出的最小距离else 将P的前⌈n/2⌉个点复制到Pl将Q的前⌈n/2⌉个点复制到Ql  将P中余下的⌊n/2⌋个点复制到Pr将Q中余下的⌊n/2⌋个点复制到Qrdl <- EfficientClosePair(Pl,Ql)dr <- EfficientClosePair(Pr,Qr)d <- min{dl,dr}m <- P[⌈n/2⌉-1].x将Q中所有[x-m|<d的点复制到数组S[0..num-1]dminsq <- d的平方for i<-0 to num-2 dok <- i+1while k<=num-1 and (S[k].y-S[i].y)的平方 < dminsqdminsq < min((S[k].x-S[i].x)^2+(S[k].y-S[i].y)^2),dminsq)k <- k+1return sqrt(dminsq)

Java代码实现

package com.算法.分治法;import java.util.ArrayList;import java.util.Comparator;import java.util.List;/** * @Author Lanh **/public class 最近对问题 {    public static void main(String[] args) { int[][] matrix = {{12,5},{23,1},{3,27},{65,4},{2,5}}; List<Node> P = new ArrayList<>(); for (int[] ints : matrix) P.add(new Node(ints[0], ints[1])); List<Node> Q = new ArrayList<>(P); P.sort(Comparator.comparingInt(o -> o.x)); Q.sort(Comparator.comparingInt(o -> o.y)); double d = ClosestPoints(P, Q); System.out.println("最近距离："+d);    }    public static double ClosestPoints(List<Node> P,List<Node> Q){ if (P.size()<=3){     int n = P.size();     double d = Double.MAX_VALUE;     for (int i=0;i<n;i++){  int x1 = P.get(i).x;  int y1 = P.get(i).y;  for (int j=i+1;j<n;j++){      int x2 = P.get(j).x;      int y2 = P.get(j).y;      d = Math.min(d,Math.pow(x1-x2,2)+Math.pow(y1-y2,2));  }     }     return d; }else {     List<Node> pl = P.subList(0,P.size()/2+1);     List<Node> pr = P.subList(P.size()/2+1, P.size());     List<Node> ql = Q.subList(0, Q.size()/2+1);     List<Node> qr = Q.subList(Q.size()/2+1, P.size());     double d = Math.min(ClosestPoints(pl,ql),ClosestPoints(pr,qr));     int m = P.get(P.size()/2).x;     List<Node> S = new ArrayList<>();     for (Node node : Q) {  if (node.x - m < d) S.add(node);     }     double dminsq = Math.pow(d,2);     for (int i=0;i<S.size()-1;i++){  int k=i+1;  while (k<S.size()&&Math.pow((S.get(k).y-S.get(i).y),2)<dminsq){      dminsq=Math.min(Math.pow((S.get(k).y-S.get(i).y),2)+Math.pow((S.get(k).x-S.get(i).x),2),dminsq);      k++;  }     }     return Math.sqrt(dminsq); }    }    static class Node{ int x;int y; Node(int x,int y){     this.x = x;     this.y = y; } @Override public String toString() {     return "Node{" +      "x=" + x +      ", y=" + y +      '}'; }    }}

测试

测试用例：{{12,5},{23,1},{3,27},{65,4},{2,5}}
测试结果：