目录

一、状态压缩DP

1.糖果（2019年省赛）

 2.矩阵计数

二、树状DP

3.生命之树

 4.大臣的旅费

5.蓝桥舞会

三.区间DP

1.石子合并  

 2.制作回文串

 3.最少操作次数 

一、状态压缩DP

1.糖果（2019年省赛）

题目描述

糖果店的老板一共有 M 种口味的糖果出售。为了方便描述，我们将 M 种口味编号 1∼ M。

小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果，而是 K 颗一包整包出售。

幸好糖果包装上注明了其中 K 颗糖果的口味，所以小明可以在买之前就知道每包内的糖果口味。

给定 NN 包糖果，请你计算小明最少买几包，就可以品尝到所有口味的糖果。

输入描述

第一行包含三个整数 N,M,K。

接下来 N 行每行 K 个整数 TT1​,T2​,⋅⋅⋅,TK​，代表一包糖果的口味。

其中，1≤N≤100,1≤M≤20,1≤K≤20,1≤Ti​≤M。

输出描述

输出一个整数表示答案。如果小明无法品尝所有口味，输出 −1。

样例输入

6 5 31 1 21 2 31 1 32 3 55 4 25 1 2

样例输出

2

N, M, K = [int(i) for i in input().split()]tot = 1 << Mdp = [-1 for _ in range(1 << 20)]dp[0] = 0kw = []# 输入数据for _ in range(N):    kw.append([int(i) for i in input().split()]) for c in kw:    tmp = 0    for x in c: tmp |= (1 < dp[i] + 1):     dp[newcase] = dp[i] + 1print(dp[tot-1])

 2.矩阵计数

N, M = list(map(int, input().split()))state = 2  Mrow = []for i in range(state):    num, flag = 0, False    temp = i    while temp: if temp & 1:     num += 1 else:     num = 0 if num == 3:     flag = True     break temp >>= 1    if not flag: row.append(i)dp = [[[0 for _ in range(state)] for __ in range(state)] for ___ in range(N)]for i in row:    dp[0][i][0] = 1for i in range(1, N):    for j in row: for k in row:     for p in row:  if j & k & p == 0:      dp[i][j][k] += dp[i - 1][k][p]ans = 0for i in row:    ans += sum(dp[N - 1][i])print(ans)

二、树状DP

3.生命之树

题目描述

在 X 森林里，上帝创建了生命之树。

他给每棵树的每个节点（叶子也称为一个节点）上，都标了一个整数，代表这个点的和谐值。

上帝要在这棵树内选出一个非空节点集 S，使得对于 S 中的任意两个点 a,b，都存在一个点列  使得这个点列中的每个点都是 S 里面的元素，且序列中相邻两个点间有一条边相连。

在这个前提下，上帝要使得 S 中的点所对应的整数的和尽量大。

这个最大的和就是上帝给生命之树的评分。

经过 atm 的努力，他已经知道了上帝给每棵树上每个节点上的整数。但是由于 atm 不擅长计算，他不知道怎样有效的求评分。他需要你为他写一个程序来计算一棵树的分数。

输入描述

第一行一个整数 n 表示这棵树有 n 个节点。

第二行 n 个整数，依次表示每个节点的评分。

接下来 n−1 行，每行 2 个整数 u,v，表示存在一条 u 到 v 的边。由于这是一棵树，所以是不存在环的。

其中，0<n≤10^5, 每个节点的评分的绝对值不超过 10^6。

输出描述

输出一行一个数，表示上帝给这棵树的分数。

样例输入

51 -2 -3 4 54 23 11 22 5

样例输出

8

def dfs(u):     global res     vis[u]=1     for son in tree[u]:   if vis[son]==1: continue   dfs(son)   if dp[son]>0: dp[u]+=dp[son]     res=max(res,dp[u])n=int(input())vis=[0 for i in range(n+1)]dp=[0 for i in range(n+1)]res=0dp[1:n]=map(int,input().split())tree=[[] for i in range(n+1)]for i in range(n-1):     u,v=map(int,input().split())     tree[u].append(v)     tree[v].append(u)dfs(1)print(res)

 4.大臣的旅费

题目描述

很久以前，T 王国空前繁荣。为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。

为节省经费，T 国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。（说明这是一个树形）

J 是 T 国重要大臣，他巡查于各大城市之间，体察民情。所以，从一个城市马不停蹄地到另一个城市成了 J 最常做的事情。他有一个钱袋，用于存放往来城市间的路费。

聪明的 J 发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第 x 千米到第 x +1 千米这一千米中（ x 是整数），他花费的路费是 x +10 这么多。也就是说走 1 千米花费 11，走 2 千米要花费 23。(x*10+x(x+1)/2)

J 大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入描述

输入的第一行包含一个整数 n，表示包括首都在内的 T 王国的城市数。

城市从 1 开始依次编号，1 号城市为首都。

接下来 n -1 行，描述 T 国的高速路（ T 国的高速路一定是 n -1 条）。

每行三个整数 Pi​,Qi​,Di​，表示城市iPi​ 和城市 Qi​ 之间有一条高速路，长度为 Di​ 千米。

输出描述

输出一个整数，表示大臣 J 最多花费的路费是多少。

样例输入

51 2 21 3 12 4 52 5 4

样例输出

135

样例说明

大臣 J 从城市 4 到城市 5 要花费 135 的路费。

def dfs(u):     global maxlen     vis[u]=1     for son,edge in tree[u]:   if vis[son]==1: continue   dfs(son)   maxlen=max(maxlen,dp[u]+dp[son]+edge)   dp[u]=max(dp[u],dp[son]+edge)n=int(input())tree=[[] for i in range(n+1)]for i in range(n-1):     a,b,c=map(int,input().split())     tree[a].append((b,c))     tree[b].append((a,c))maxlen=0vis=[0 for i in range(n+1)]dp=[0 for i in range(n+1)]dfs(1)print(maxlen*10+(maxlen+1)*maxlen//2)

5.蓝桥舞会

题目描述

蓝桥公司一共有 n 名员工，编号分别为 1∼n。

他们之间的关系就像一棵以董事长为根的树，父节点就是子节点的直接上司。

每个员工有一个快乐指数 ai​。

现蓝桥董事会决定举办一场蓝桥舞会来让员工们在工作之余享受美好时光，不过对于每个员工，他们都不愿意与自己的直接上司一起参会。

董事会希望舞会的所有参会员工的快乐指数总和最大，请你求出这个最大值。

输入描述

输入的第一行是一个整数 n，表示蓝桥公司的员工数。

第二行包含 n 个整数，分别表示第 i 个员工的快乐指数 ai​。

接下来 n−1 行每行包含两个整数 u,v，表示 v 是u 的直接上司。

1≤u,v,ai​≤n≤105

输出描述

输出一个整数，表示答案。

样例输入

51 1 1 1 11 32 34 53 5

样例输出

3

样例说明

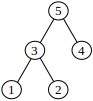
下图是样例的树结构。结点选 1、2、5 时，有最大值 3。

图 样例的树型关系

根据DP 的解题思路，我们定义某个结点 uu 的状态为：

• dp[u][0]：不选择结点 u 时，以 u 为根的子树的最优解，即这棵子树的最大值。
• dp[u][1]：选择结点 u 时，以 u 为根的子树的最优解

• 不选择结点u ：那么它的子结点son 可选可不选，我们取其中的最大值，状态转移方程为：dp[u][0] += max(dp[son][1], dp[son][0])
• 选择结点u：那么它的子结点不能选，状态转移方程为：dp[u][1] += dp[son][0];

  n=int(input())value=[0 for i in range(n+1)]value[1:n+1]=map(int,input().split())tree=[[] for i in range(n+1)]father=[-1 for i in range(n+1)]dp=[[0 for i in range(2)]for j in range(n+1)]for i in range(n-1):     a,b=map(int,input().split())     tree[b].append(a)     father[a]=bfor i in range(1,n+1):     if father[i]==-1:   root=i   breakdef dfs(u):     dp[u][1]=value[u]     dp[u][0]=0     for son in tree[u]:   dfs(son)   dp[u][1]+=dp[son][0]   dp[u][0]+=max(dp[son][0],dp[son][1])dfs(root)print(max(dp[root][1],dp[root][0]))

  ---

  三.区间DP

• 1.石子合并  

题目描述

有 n 堆石子排成一排，每堆石子有一定的数量。现在我们要将 n 堆石子并成为一堆，每次只能合并相邻的两堆石子，合并的花费为这两堆石子的总数。经过 n−1 次合并后会成为一堆，求总的最小花费。

输入描述

第一行输入一个 n ,代表文档的数量。

第二行输入 n 个整数 a1​,a2​,a3​...an​ ，ai​ 代表第 ii 堆石子的数量 。

1≤n≤100,1≤ai​≤105。

输出描述

输出一个整数，表示答案。

样例输入

44 5 9 4

样例输出

44

• 状态的定义很直接：定义 dp[i][j]dp[i][j] 为合并第 ii 堆到第 jj 堆的最小花费。
• 对于状态转移方程呢：从第 ii 堆合并到第 jj 堆即：dp[i][j] = min(dp[i][k] + dp[k + 1][j] + w[i][j]) （i\leq k < ji≤k<j，w[i][j]w[i][j] 表示从第 ii 堆到第 jj 堆的石子总数）。
• 答案：dp[1][n]。

我们按自顶向下的思路分析即可。计算大区间 [i, j][i,j] 的最优值时，合并它的两个子区[i,k] 和 [k+1, j]，对所有可能的合并（i≤k<j ，即 k 在 i 、j 之间滑动），返回那个最优的合并。子区间再继续分解为更小的区间，最小的区间[i,i+1] 只包含两堆石子。我画了几个图，下面就用这些图说明这个转移过程。

为了计算最后的 dp[1][n]，需要考虑所有可能的合并。这些合并包括：

1. 合并之前 dp[i][i] = 0，1≤i≤n;

2. 两堆合并

   

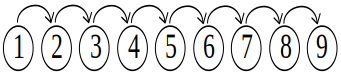
   • 例如：dp[1][2] = dp[1][1] + dp[2][2] + w[1][2];
   • 总结：dp[i][i+1] = dp[i][i] + dp[i+1][i+1] + w[i][i+1]；

3. 三堆合并

   

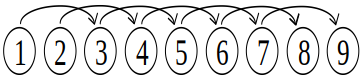
   • 例如：合并第 1 堆到第 3 堆，有 2种情况： 

     

     dp[1][3] = min(dp[1][1]+dp[2][3],dp[1][2]+dp[3][3])+w[1][3];

   • 总结：dp[i][i+2]=min(dp[i][i]+dp[i+1][i+2],dp[i][i+1]+dp[i+2][i+2])+w[i][i+2];

4. 推广 第i堆到第 j 堆的合并： dp[i][j] = min(dp[i][k]+dp[k+1][j]) + w[i][j-i+1]，i≤k≤j。这就是状态转移方程。

用自底向上递推的方法，先在小区间进行DP 得到最优解，然后再逐步合并小区间为大区间

n=int(input())a=[0 for i in range(n+1)]a[1:n+1]=map(int,input().split())w=[[0 for i in range(n+1)]for j in range(n+1)]dp=[[0 for i in range(n+1)]for j in range(n+1)]for i in range(1,n):     for j in range(i,n+1):   w[i][j]=sum(a[i:j+1])for i in range(1,n+1):     dp[i][i]=0for l in range(1,n):     for i in range(1,n-l+1):   j=i+l   dp[i][j]=float('inf')   for k in range(i,j): dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+w[i][j])print(dp[1][n])

 2.制作回文串

题目描述

给定字符串 S，长度为 M，由 N 个小写字母构成。在 S 的任意位置增删字母，把它变为回文串。删特定字母的花费不同。求最小花费。

输入描述

输入的第一行包含两个整数 N,M，分别表示字符串种类数和字符串长度 M；

第二行包含一个字符串 S。

接下来 N 行每行分别给出每个字符插入和删除的花费。

1≤N≤26，1≤M≤2×103。

保证删除和插入的最大花费都不超过 10^4。

输出描述

输出一个整数，表示答案。

样例输入

3 4abcba 1000 1100b 350 700c 200 800

样例输出

900

样例说明

上述样例中，如果在结尾处插入“a”，得到“abcba”，花费 1000；如果在首端删除 “a” 得到 “bcb”，花费 1100；如果在首端插入“bcb”，花费 350 + 200 + 350 = 900，即最小值。

 求最少修改次数，那么把 S 反转得到 S′，求得两者最长公共子序列的长度 L，用 S 的长度减去 L 就是答案。

区间 DP 求解最小花费：首先定义状态 dp[i][j]dp[i][j] 表示字符串 ss 的子区间 s[i, j]s[i,j] 变成回文的最小花费。然后对于删除和插入的花费，由于这两种操作是等价的，即这头加和那头减一样，所以只要取这两种操作的最小值就行了（用数组 w[]w[] 定义字符的花费）。那么现在有以下三种情况：

1. 如果 s[i]==s[j]，那么 dp[i][j]=dp[i+1][j−1]。

   

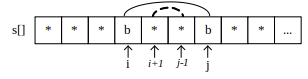
2. 如果 dp[i+1][j] 是回文串，那么 dp[i][j]=dp[i+1][j]+w[i]。

   

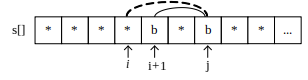
3. 如果 dp[i][j−1] 是回文串，那么 dp[i][j]=dp[i][j−1]+w[j]。

总结情况 2、3，可得状态转移方程为dp[i][j]=min(dp[i+1][j]+w[i],dp[i][j−1]+w[j])。

下面是我的代码。代码中包含两层循环，外层 i 枚举子区间起点，内层 j 枚举终点。因为需要从小区间扩展到大区间，所以 i 从 s 的尾端开始，逐步回退扩大区间，直到首端。

n,m=map(int,input().split())s=input()dice={}dp=[[0 for i in range(m+1)]for j in range(m+1)]for i in range(n):     ch,x,y=map(str,input().split())     x=int(x)     y=int(y)     dice[ch]=min(x,y)for i in range(m-2,-1,-1):     for j in range(i+1,m):   if s[i]==s[j]: dp[i][j]=dp[i+1][j-1]   else: dp[i][j]=min(dp[i+1][j]+dice[s[i]],dp[i][j-1]+dice[s[j]])print(dp[0][m-1])

 3.最少操作次数

题目描述

给定两个长度相等的字符串 A、B，由小写字母组成。

现有一种操作，可以把 A 中的一个连续子串（区间）都转换为某个字符（就像用刷子刷成一样的字符）。

问要把 A 转换为 B，最少的操作数是多少?

输入描述

输入共两行，第一行是字符串 A，第二行是字符串 B。

1≤∣A∣,∣B∣≤100。

输出描述

输出一个整数，表示答案。

样例输入

qwerqwerqqorzorzoorz

样例输出

7

其中的重点是区间 [i,j] 两端的字符 B[i] 和B[j]，我们分析以下两种情况：

1. B[i]=B[j]： 第一次刷用 B[i] 把区间 [i,j] 刷一遍，这个刷法肯定是最优的。如果分别去掉两个端点，得到 2 个区间 [i+1,j]、[i, j-1]，那这 2 个区间的最小步数相等，也等于原区间 [[i,j] 的最小步数。例如 B[i,j]=abbba，先用 "a" 全部刷一遍，再刷 1次 bbb"，共刷 2 次。如果去掉第一个 "a"，剩下的 "bbba"，也是刷 2 次。
2. B[i] ≠ B[j]。因为两端点不等，至少要各刷 1 次。用标准的区间操作，把区间分成 [i, k] 和[k+1,j] 两部分，枚举最小步数即可。

接下来我们再考虑从 A 转换到 B。那么如何求 dp[1][j] 呢？观察 A 和 B 相同位置的字符，我们可对以下两种情况进行分析：

1. 若 A[j]=B[j]：这时字符不用转换，有 dp[1][j]=dp[1][j−1]。
2. 若 A[j] ≠ B[j]。仍然用标准的区间 DP，把区间分成 [1, k][1,k] 和 [k+1, j][k+1,j] 两部分，枚举最小步数。这里利用了上一步从空白转换到 B 的结果，当区间[k+1, j][k+1,j] 内 A 和 B 的字符不同时，从 A 转到 B，与从空白串转换到 B 是等价的。

A=[0 for i in range(105)]B=[0 for i in range(105)]dp=[[float('inf') for i in range(105)]for j in range(105)]a=input()b=input()for i in range(1,len(a)+1):     A[i]=a[i-1]for i in range(1,len(b)+1):     B[i]=b[i-1]n=len(a)for i in range(1,len(a)+1):     dp[i][i]=1for len in range(2,n+1):     for i in range(1,n-len+2):   j=i+len-1   if B[i]==B[j]: dp[i][j]=dp[i+1][j]   else: for k in range(i,j):      dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j])for j in range(1,n+1):     if A[j]==B[j]:   dp[1][j]=dp[1][j-1]     else:   for k in range(1,j): dp[1][j]=min(dp[1][j],dp[1][k]+dp[k+1][j])print(dp[1][n])