1.1 一维数组
数组是最简单的,也最基础的数据结构。数组是一个有序的数据集合,用索引(或者叫下标)访问数据。在大多数编程语言,比如C/C++/java/javascript中,数组的索引都是以0开始。它的逻辑结构是一段连续的空间(因为虚拟内存的原因,实际情况下大数组可能由多个不连续的内存页组成)。
如下图所示:
|
1 |
1 |
2 |
3 |
5 |
8 |
|
0 |
1 |
2 |
3 |
4 |
5 |
上图中,第一行表示数据第二行表示索引
一维数组,我会以一个案例来开始。
假设有这么一个需求,求11个点能构成多少种二叉树。比如3个点,可以构成五种二叉树:
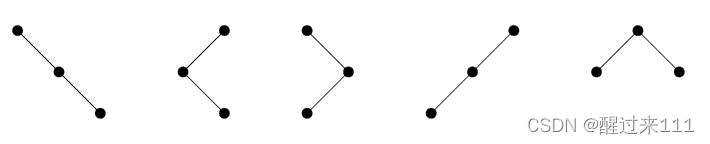
按照序言里的步骤,我们第一步是仔细研究需求。从上图看,所有的树都是线性结构。那么不同在哪里?可见这个问题其实是数学里的组合计数问题。
解题思路
以3个点为例子,作为二叉树必须要有根节点。那么利用分类归纳法,可以这样计算出来。
场景1 只有左节点
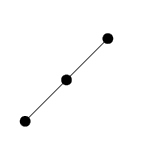
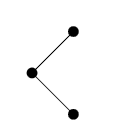
场景2 左右节点都存在
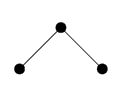
场景3 只有右节点
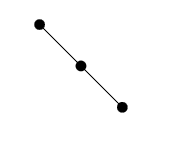
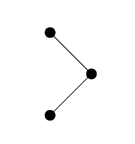
以上场景实际上是什么问题?
是结点的左右分配问题!那么假设N个结点能组成二叉树的数目为C(n)
场景1
左节点数量2,右节点数量0,树的数量为左边树的数量C(2)*右边树的数量 C(0)
场景2
左节点数量1,右节点数量1,树的数量为左边树的数量C(1)*右边树的数量 C(1)
场景3
左节点数量0,右节点数量2,树的数量为左边树的数量C(0)*右边树的数量 C(2)
所以对于N个结点,就可以分成N种场景。左边的数目确定了,右边的数目就也确定了。所以可以写出递归公式,是乘积的求和:
![]()
那么这个问题,用什么数据结构呢?根据递归公式,可以清楚地知道我们需要存储C(0)到C(n-1)的所有数据,所以这个问题,一维数组这种数据结构最合适了。经过分析之后,代码就非常容易写了。
Python代码
def c(n): if n < 2: return 1 array = [0] * (n + 1) array[1] = array[0] = 1 for i in range(2, n + 1): for j in range(0, i): array[i] += array[j] * array[i - j - 1] return array[n]需要注意的是python中没有严格意义上的数组。为了严谨,这里附上java代码:
public static int catalan(int n) { if (n < 2) { return 1; } int[] array = new int[n + 1]; array[1] = array[0] = 1; for (int i = 2; i < n + 1; i++) { for (int j = 0; j < i; j++) { array[i] += array[j] * array[i - j - 1]; } } return array[n]; }这个数列就是著名的明安图数列,也叫卡特兰数列。不过在我们这个例子中,与卡特兰数列错了一位而已。
我们的例子中c(0)=1 c(1)=1 c(2)=2……
而卡特兰数列是c(1)=1 c(2)=1 c(3)=2……
递归公式,与卡特兰数列一模一样。
这个题目属于数学专业研究生的组合计数学课程。其实我是反对把知识分什么中学知识、大学知识、硕士阶段、博士阶段的。我们要做的仅仅是,按照编程的套路,先仔细分析需求,选择合适的数据结构,然后设计算法,编写代码,就可以了。


