NC刷题笔记10-动态规划

NC刷题笔记10-动态规划

• • BM62 斐波那契数列
  • BM63 跳台阶
  • BM64 最小花费爬楼梯
  • BM65 最长公共子序列(二)
  • BM66 最长公共子串
  • BM67 不同路径的数目(一)
  • BM68 矩阵的最小路径和
  • BM69 把数字翻译成字符串
  • BM70 兑换零钱(一)
  • BM71 最长上升子序列(一)
  • BM72 连续子数组的最大和
  • BM73 最长回文子串
  • BM74 数字字符串转化成IP地址
  • BM75 编辑距离(一)
  • BM76 正则表达式匹配
  • BM77 最长的括号子串
  • BM78 打家劫舍(一)
  • BM79 打家劫舍(二)
  • BM80 买卖股票的最好时机(一)
  • BM81 买卖股票的最好时机(二)
  • BM82 买卖股票的最好时机(三)

BM62 斐波那契数列

思路：递归非递归

public class Solution {    public int Fibonacci(int n) { if(n<=2) return 1; return Fibonacci(n-1)+Fibonacci(n-2);    }}

public class Solution {    public int Fibonacci(int n) { if(n<=2) return 1; int a=1,b=1,sum=a+b; for(int i=3;i<=n;i++){     sum=a+b;     a=b;     b=sum; } return sum;    }}

BM63 跳台阶

描述一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。数据范围：1≤n≤40要求：时间复杂度：O(n) ，空间复杂度： O(1)示例1输入：2返回值：2说明：青蛙要跳上两级台阶有两种跳法，分别是：先跳一级，再跳一级或者直接跳两级。因此答案为2示例2输入：7返回值：21

public class Solution {    public int jumpFloor(int target) { if(target<=1) return 1; int a=1,b=1,sum=a+b; for(int i=2;i<=target;i++){     sum=a+b;     a=b;     b=sum; } return sum;    }}

BM64 最小花费爬楼梯

描述给定一个整数数组 cost   ，其中 cost[i]是从楼梯第i个台阶向上爬需要支付的费用，下标从0开始。一旦你支付此费用，即可选择向上爬一个或者两个台阶。你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。数据范围：数组长度满足 1≤n≤10^5，数组中的值满足 1≤cost≤10^4  示例1输入：[2,5,20]返回值：5说明：你将从下标为1的台阶开始，支付5 ，向上爬两个台阶，到达楼梯顶部。总花费为5   示例2输入：[1,100,1,1,1,90,1,1,80,1]返回值：6说明：你将从下标为 0 的台阶开始。1.支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。2.支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。3.支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。4.支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。5.支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。6.支付 1 ，向上爬一个台阶，到达楼梯顶部。总花费为 6 。

import java.util. ;public class Solution {    public int minCostClimbingStairs (int[] cost) { int n=cost.length; if(n==1||n==2) return 0; int[] dp=new int[n+1]; dp[0]=0; dp[1]=0; for(int i=2;i<=n;i++){     dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]); } return dp[n];    }}

BM65 最长公共子序列(二)

描述给定两个字符串str1和str2，输出两个字符串的最长公共子序列。如果最长公共子序列为空，则返回"-1"。目前给出的数据，仅仅会存在一个最长的公共子序列数据范围：0≤∣str1∣,∣str2∣≤2000要求：空间复杂度 O(n^2)，时间复杂度 O(n^2)示例1输入："1A2C3D4B56","B1D23A456A"返回值："123456"示例2输入："abc","def"返回值："-1"示例3输入："abc","abc"返回值："abc"示例4输入："ab",""返回值："-1"

import java.util. ;public class Solution {    public String LCS (String s1, String s2) { int n=s1.length(); int m=s2.length(); String[][] dp=new String[n+1][m+1]; for(int i=0;i<=n;i++){     for(int j=0;j<=m;j++){  if(i==0||j==0){      dp[i][j]="";  }else if(s1.charAt(i-1)==s2.charAt(j-1)){      dp[i][j]=dp[i-1][j-1]+s1.charAt(i-1);  }else{      dp[i][j]=dp[i-1][j].length()>dp[i][j-1].length()?dp[i-1][j]:dp[i][j-1];  }     } } return dp[n][m]==""?"-1":dp[n][m];    }}

BM66 最长公共子串

描述给定两个字符串str1和str2,输出两个字符串的最长公共子串题目保证str1和str2的最长公共子串存在且唯一。 数据范围：1≤∣str1∣,∣str2∣≤5000要求： 空间复杂度 O(n^2)，时间复杂度 O(n^2)示例1输入："1AB2345CD","12345EF"返回值："2345"备注：1≤∣str1∣,∣str2∣≤5000

思路：动态规划某位置上相等： dp[i + 1][j + 1] = dp[i][j] + 1;某位置上不等： dp[i + 1][j+1] = 0;

public String LCS(String str1, String str2) {    int maxLenth = 0;//记录最长公共子串的长度    //记录最长公共子串最后一个元素在字符串str1中的位置    int maxLastIndex = 0;    int[][] dp = new int[str1.length() + 1][str2.length() + 1];    for (int i = 0; i < str1.length(); i++) { for (int j = 0; j < str2.length(); j++) {     //递推公式，两个字符相等的情况     if (str1.charAt(i) == str2.charAt(j)) {  dp[i + 1][j + 1] = dp[i][j] + 1;  //如果遇到了更长的子串，要更新，记录最长子串的长度，  //以及最长子串最后一个元素的位置  if (dp[i + 1][j + 1] > maxLenth) {      maxLenth = dp[i + 1][j+1];      maxLastIndex = i;  }     } else {  //递推公式，两个字符不相等的情况  dp[i + 1][j+1] = 0;     } }    }    //最字符串进行截取，substring(a,b)中a和b分别表示截取的开始和结束位置    return str1.substring(maxLastIndex - maxLenth + 1, maxLastIndex + 1);}

BM67 不同路径的数目(一)

描述一个机器人在m×n大小的地图的左上角（起点）。机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。可以有多少种不同的路径从起点走到终点？备注：m和n小于等于100,并保证计算结果在int范围内   数据范围：0<n,m≤100，保证计算结果在32位整型范围内要求：空间复杂度O(nm)，时间复杂度O(nm)进阶：空间复杂度O(1)，时间复杂度O(min(n,m))示例1输入：2,1返回值：1示例2输入：2,2返回值：2

思路：动态规划：dp[i][j]=dp[i-1][j]+dp[i][j-1];每个位置只会从左边或者上边过来

import java.util. ;public class Solution {    public int uniquePaths (int m, int n) { int[][] dp=new int[m+1][n+1]; for(int i=1;i<=m;i++){     for(int j=1;j<=n;j++){  if(i==1||j==1){      dp[i][j]=1;  }else{      dp[i][j]=dp[i-1][j]+dp[i][j-1];  }     } } return dp[m][n];    }}

BM68 矩阵的最小路径和

描述给定一个 n   m 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。数据范围: 1≤n,m≤500，矩阵中任意值都满足0≤ai,j≤100要求：时间复杂度 O(nm)例如：当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时，对应的返回值为12，所选择的最小累加和路径如下图所示：

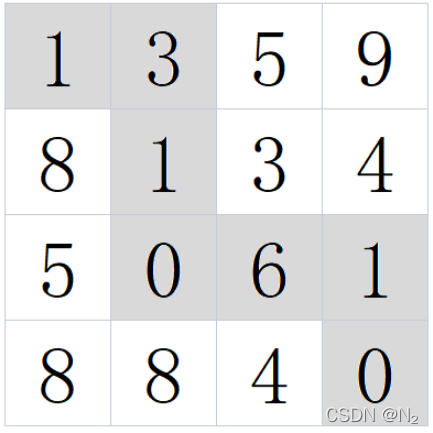
示例1输入：[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]返回值：12示例2输入：[[1,2,3],[1,2,3]]返回值：7

思路：动态规划1 上边只能从左边过来2 左边只能从上边过来3 其他的可以从上左两个方向过来

import java.util. ;public class Solution {    public int minPathSum (int[][] matrix) { if(matrix==null||matrix.length==0) return 0; int n=matrix.length; int m=matrix[0].length; int[][] dp=new int[n+1][m+1]; for(int i=1;i<=n;i++){     for(int j=1;j<=m;j++){  if(i==1){      dp[i][j]=dp[i][j-1]+matrix[i-1][j-1];  }else if(j==1){      dp[i][j]=dp[i-1][j]+matrix[i-1][j-1];  }else{      dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+matrix[i-1][j-1];  }     } } return dp[n][m];    }}

BM69 把数字翻译成字符串

描述有一种将字母编码成数字的方式：'a'->1, 'b->2', ... , 'z->26'。现在给一串数字，返回有多少种可能的译码结果数据范围：字符串长度满足0<n≤90进阶：空间复杂度O(n)，时间复杂度O(n)示例1输入："12"返回值：2说明：2种可能的译码结果（”ab” 或”l”）  示例2输入："31717126241541717"返回值：192说明：192种可能的译码结果

动态规划:四种情况1 无法翻译 当前为0 前面的>2或前面也为02 只能组合翻译 当前为0 前面为1或23 只能单独翻译 当前>6 前面为0或者前面>24 可以组合翻译 dp[i]=dp[i-1]+dp[i-2]

import java.util. ;public class Solution {    public int solve (String nums) { if(nums==null ||nums.length()==0) return 0; int[] dp = new int[nums.length()+1]; dp[0]=1; dp[1]=nums.charAt(0)=='0'?0:1; for(int i=2;i<dp.length;i++){     //无法独立编码也无法组合编码     if(nums.charAt(i-1)=='0' && (nums.charAt(i-2)=='0' || nums.charAt(i-2)>'2')){  return 0;     //只能组合编码     }else if(nums.charAt(i-1)=='0'){  dp[i] = dp[i-2];     //只能独立编码     }else if(nums.charAt(i-2)=='0' || nums.charAt(i-2)>'2' || nums.charAt(i-2)=='2'&& nums.charAt(i-1)>'6' ){  dp[i] = dp[i-1];     //两种编码方式都可以     }else{  dp[i] = dp[i-1]+dp[i-2];     } } return dp[nums.length()];    }}

BM70 兑换零钱(一)

描述给定数组arr，arr中所有的值都为正整数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，再给定一个aim，代表要找的钱数，求组成aim的最少货币数。 如果无解，请返回-1.数据范围：数组大小满足0≤n≤10000 ， 数组中每个数字都满足0<val≤10000，0≤aim≤5000要求：时间复杂度O(n×aim) ，空间复杂度O(aim)示例1输入：[5,2,3],20返回值：4示例2输入：[5,2,3],0返回值：0示例3输入：[3,5],2返回值：-1

思路：动态规划dp[i] = Math.min(dp[i],dp[i-arr[j]] + 1);

import java.util. ;public class Solution {    public int minMoney (int[] arr, int aim) { int Max = aim + 1;//定一个全局最大值 int []dp = new int[aim + 1];//dp[i]的含义是目标值为i的时候最少钱币数是多少。 Arrays.fill(dp,Max);//把dp数组全部定为最大值 dp[0] = 0;//总金额为0的时候所需钱币数一定是0 for(int i = 1;i <= aim;i ++){// 遍历目标值     for(int j = 0;j < arr.length;j ++){// 遍历钱币  if(arr[j] <= i){//如果当前的钱币比目标值小就可以兑换      dp[i] = Math.min(dp[i],dp[i-arr[j]] + 1);  }     } } return dp[aim] > aim ? -1 : dp[aim];    }}

BM71 最长上升子序列(一)

描述给定一个长度为 n 的数组 arr，求它的最长严格上升子序列的长度。所谓子序列，指一个数组删掉一些数（也可以不删）之后，形成的新数组。例如 [1,5,3,7,3] 数组，其子序列有：[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。我们定义一个序列是 严格上升 的，当且仅当该序列不存在两个下标 i 和 j 满足 i<j 且 arri≥arrj。数据范围： 0≤n≤1000要求：时间复杂度 O(n^2)， 空间复杂度 O(n)示例1输入：[6,3,1,5,2,3,7]返回值：4说明：该数组最长上升子序列为 [1,2,3,7] ，长度为4

思路：动态规划遍历0到i-1位置的元素，如果有小于i位置的元素 则dp[i]=Math.max(dp[i],dp[j]+1);返回最大值即可

import java.util. ;public class Solution {    public int LIS (int[] arr) { if(arr==null||arr.length==0) return 0; int maxLen=1; int[] dp=new int[arr.length]; Arrays.fill(dp,1); for(int i=1;i<dp.length;i++){     for(int j=i-1;j>=0;j--){  if(arr[i]>arr[j]){      dp[i]=Math.max(dp[i],dp[j]+1);  }     }     maxLen=Math.max(maxLen,dp[i]); } return maxLen;    }}

BM72 连续子数组的最大和

描述输入一个长度为n的整型数组array，数组中的一个或连续多个整数组成一个子数组，子数组最小长度为1。求所有子数组的和的最大值。数据范围:1<=n<=2 10^5 , −100<=a[i]<=100要求:时间复杂度为 O(n)，空间复杂度为 O(n)进阶:时间复杂度为 O(n)，空间复杂度为 O(1)示例1输入：[1,-2,3,10,-4,7,2,-5]返回值：18说明：经分析可知，输入数组的子数组[3,10,-4,7,2]可以求得最大和为18 示例2输入：[2]返回值：2示例3输入：[-10]返回值：-10

思路1：动态规划 dp[i]=array[i-1]+((dp[i-1]>0)?dp[i-1]:0);时间复杂度O(n) 空间复杂度 O(n)思路2：思路1的改进，dp状态只需要1个，前一个元素的dp值

public class Solution {    public int FindGreatestSumOfSubArray(int[] array) { if(array==null || array.length==0) return 0; int[] dp=new int[array.length+1]; int maxres=Integer.MIN_VALUE; for(int i=1;i<=array.length;i++){     dp[i]=array[i-1]+((dp[i-1]>0)?dp[i-1]:0);     maxres=Math.max(maxres,dp[i]); } return maxres;    }}

public class Solution {    public int FindGreatestSumOfSubArray(int[] array) { if(array==null || array.length==0) return 0; int b=0; int maxSum=Integer.MIN_VALUE; for(int i=0;i<array.length;i++){     b=array[i]+(b>0?b:0);     maxSum=Math.max(b,maxSum); } return maxSum;    }}

BM73 最长回文子串

描述对于长度为n的一个字符串A（仅包含数字，大小写英文字母），请设计一个高效算法，计算其中最长回文子串的长度。数据范围：1≤n≤1000要求：空间复杂度 O(1)，时间复杂度 O(n^2)进阶:  空间复杂度 O(n)，时间复杂度 O(n)示例1输入："ababc"返回值：3说明：最长的回文子串为"aba"与"bab"，长度都为3示例2输入："abbba"返回值：5示例3输入："b"返回值：1

思路1：中心扩散法，需要判断 双数和单数两种情况时间复杂度：O(N^2)，空间复杂度：O(1)思路2：双层for循环+双指针时间复杂度：O(N^2)，空间复杂度：O(1)思路3：动态规划两层for循环dp[left][right] = dp[left + 1][right - 1];时间复杂度：O(N^2)，空间复杂度：O(N^2)

import java.util. ;public class Solution {    public int getLongestPalindrome(String A) { char[] chars=A.toCharArray(); int maxLength=0; for(int i=0;i<chars.length;i++){     maxLength=Math.max(maxLength,getLength(i,chars)); } return maxLength;    } public int getLength(int i,char[] chars){ //单数 int res=1,left=i-1,right=i+1; while(left>=0 && right<chars.length){     if(chars[left]==chars[right]){  res+=2;  left--;  right++;     }else{  break;     } } //双数 int res0=0; if((i+1)<chars.length && chars[i]==chars[i+1]){     left=i;     right=i+1;     while(left>=0 && right<chars.length){  if(chars[left]==chars[right]){      res0+=2;      left--;      right++;  }else{      break;  }} } return Math.max(res,res0);    }}

import java.util. ;public class Solution {    public int getLongestPalindrome(String A) { char[] chars=A.toCharArray(); int maxlength=0; for(int i=0;i<chars.length;i++){     for(int j=i;j<chars.length;j++){  if(judge(i,j,chars)) maxlength=Math.max(maxlength,j-i+1);     } } return maxlength;    } public boolean judge(int i,int j,char[] chars){ if(i==j) return true; while(i<j){     if(chars[i]!=chars[j]) return false;     i++;     j--; } return true;    }}

public int getLongestPalindrome(String A, int n) {    //边界条件判断    if (n < 2) return A.length();    //start表示最长回文串开始的位置，    //maxLen表示最长回文串的长度    int maxLen = 1;    boolean[][] dp = new boolean[n][n];    for (int right = 1; right < n; right++) { for (int left = 0; left <= right; left++) {     //如果两种字符不相同，肯定不能构成回文子串     if (A.charAt(left) != A.charAt(right)) continue;     //下面是s.charAt(left)和s.charAt(right)两个     //字符相同情况下的判断     //如果只有一个字符，肯定是回文子串     if (right == left) {  dp[left][right] = true;     } else if (right - left <= 2) {  //类似于"aa"和"aba"，也是回文子串  dp[left][right] = true;     } else {  //类似于"a      a"，要判断他是否是回文子串，只需要  //判断"      "是否是回文子串即可  dp[left][right] = dp[left + 1][right - 1];     }     //如果字符串从left到right是回文子串，只需要保存最长的即可     if (dp[left][right] && right - left + 1 > maxLen) {  maxLen = right - left + 1;     } }    }    //最长的回文子串    return maxLen;}

BM74 数字字符串转化成IP地址

描述现在有一个只包含数字的字符串，将该字符串转化成IP地址的形式，返回所有可能的情况。例如：给出的字符串为"25525522135",返回["255.255.22.135", "255.255.221.35"]. (顺序没有关系)数据范围：字符串长度 0≤n≤12  要求：空间复杂度O(n!),时间复杂度 O(n!)注意：ip地址是由四段数字组成的数字序列，格式如 "x.x.x.x"，其中 x 的范围应当是 [0,255]。示例1输入："25525522135"返回值：["255.255.22.135","255.255.221.35"]示例2输入："1111"返回值：["1.1.1.1"]示例3输入："000256"返回值："[]"

思路1：暴力枚举，每一个位包含一到三位字符如果四个位置相加为s.length思路2：递归回溯

思路1：import java.util. ;public class Solution {    public ArrayList<String> restoreIpAddresses (String s) { ArrayList<String> list = new ArrayList(); for(int a=1; a<4; a++){     for(int b=1; b<4; b++){  for(int c=1; c<4; c++){      for(int d=1; d<4; d++){   if(a+b+c+d==s.length()){String s1 = s.substring(0, a);String s2 = s.substring(a, a+b);String s3 = s.substring(a+b, a+b+c);String s4 = s.substring(a+b+c, a+b+c+d);if(check(s1)&&check(s2)&&check(s3)&&check(s4)){    String ip = s1+"."+s2+"."+s3+"."+s4;    list.add(ip);}   }      }  }     } } return list;    }    public boolean check(String s){ if(Integer.valueOf(s)<=255){     if(s.charAt(0)!='0' || s.charAt(0)=='0'&&s.length()==1)   return true; } return false;    }}

思路2：import java.util. ;public class Solution {    public ArrayList<String> restoreIpAddresses (String s) { if (s.length() > 12) {     return null; } StringBuilder sb = new StringBuilder(s); doRestoreIpAddresses(sb, 1); return ans;    }    ArrayList<String> ans = new ArrayList<>();    public void doRestoreIpAddresses(StringBuilder s, int m) { // 回溯暴力算法，还要很多地方没有剪枝 String[] nums = s.toString().split("\\."); if (nums.length > 4) { // 剪枝     return; } if (validateIPv4(s.toString())) { // 结束条件     ans.add(String.copyValueOf(s.toString().toCharArray()));     return; } for (int i = m; i < s.length(); i++) { // 回溯     s.insert(i, ".");      doRestoreIpAddresses(s, i + 2);     s.replace(i, i + 1, ""); }    }  public boolean validateIPv4(String IP) { String[] nums = IP.split("\\."); if (nums.length !=  4) {     return false; } for (String x : nums) {     // 0-255:     if (x.length() == 0 || x.length() > 3) return false;     // 0的情况     if (x.charAt(0) == '0' && x.length() != 1) return false;     // 大于255     if (Integer.parseInt(x) > 255) return false; } return true;    }}

BM75 编辑距离(一)

描述给定两个字符串 str1 和 str2 ，请你算出将 str1 转为 str2 的最少操作数。你可以对字符串进行3种操作：1.插入一个字符2.删除一个字符3.修改一个字符。字符串长度满足1≤n≤1000，保证字符串中只出现小写英文字母。示例1输入："nowcoder","new"返回值：6说明："nowcoder"=>"newcoder"(将'o'替换为'e')，修改操作1次     "nowcoder"=>"new"(删除"coder")，删除操作5次      示例2输入："intention","execution"返回值：5说明：一种方案为:因为2个长度都是9，后面的4个后缀的长度都为"tion"，于是从"inten"到"execu"逐个修改即可  示例3输入："now","nowcoder"返回值：5

思路：动态规划  int[][] dp=new int[str1.length()+1][str2.length()+1];    当前位置字符相等 dp[i+1][j+1]=dp[i][j];  当前位置字符不相等 dp[i+1][j+1]=Math.min(insert,delete,replace)int delete=dp[i+1][j]+1;  int insert=dp[i][j+1]+1;  int change=dp[i][j]+1;

import java.util. ;public class Solution {    public int editDistance (String str1, String str2) { if(str1.length()==0||str2.length()==0) return str1.length()==0?str2.length():str1.length(); int[][] dp=new int[str1.length()+1][str2.length()+1]; //特殊解 for(int i=0;i<=str1.length();i++){     dp[i][0]=i; } for(int i=0;i<=str2.length();i++){     dp[0][i]=i; }  for(int i=0;i<str1.length();i++){     for(int j=0;j<str2.length();j++){  if(str1.charAt(i)==str2.charAt(j)){      dp[i+1][j+1]=dp[i][j];  }else{      int delete=dp[i+1][j]+1;      int insert=dp[i][j+1]+1;      int change=dp[i][j]+1;      int min = change > insert ? insert : change;      min = delete > min ? min : delete;      dp[i + 1][j + 1] = min;  }     } } return dp[str1.length()][str2.length()];    }}

BM76 正则表达式匹配

描述请实现一个函数用来匹配包括'.'和' '的正则表达式。1.模式中的字符'.'表示任意一个字符2.模式中的字符' '表示它前面的字符可以出现任意次（包含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab ac a"匹配，但是与"aa.a"和"ab a"均不匹配数据范围:1.str 只包含从 a-z 的小写字母。2.pattern 只包含从 a-z 的小写字母以及字符 . 和  ，无连续的 ' '。3. 0≤str.length≤26 4. 0≤pattern.length≤26 示例1输入："aaa","a a"返回值：true说明：中间的 可以出现任意次的a，所以可以出现1次a，能匹配上示例2输入："aad","c a d"返回值：true说明：因为这里 c 为 0 个，a被重复一次，   表示零个或多个a。因此可以匹配字符串 "aad"。示例3输入："a",". "返回值：true说明：". " 表示可匹配零个或多个（' '）任意字符（'.'）示例4输入："aaab","a a a c"返回值：false

思路：动态规划1、 i和j处的字符相等 dp[i][j]=d[i-1][j-1]2、 j处为'.' dp[i][j]=d[i-1][j-1]3、 j处为' ' j-1处不为'.'  匹配成功3.1 匹配0次 dp[i][j]=dp[i][j-2] 3.2 匹配1次 dp[i][j]=d[i][j-1] 3.3 匹配n次 d[i][j]=d[i-1][j]   匹配不成功   3.4 匹配0次 dp[i][j]=dp[i][j-2] 4、j-1处为'.' j处为' '4.1 匹配0次 dp[i][j]=dp[i][j-2] 4.2 匹配1次 dp[i][j]=d[i][j-1] 4.3 匹配n次 d[i][j]=d[i-1][j]

import java.util. ;public class Solution {    public boolean match (String str, String pattern) { boolean[][] dp=new boolean[str.length()+1][pattern.length()+1]; dp[0][0]=true; for(int i=1;i<=pattern.length();i++){     //匹配0次     if (i >= 2 && pattern.charAt(i - 1) == ' ') dp[0][i] = dp[0][i - 2]; }  for(int i=1;i<=str.length();i++){     for(int j=1;j<=pattern.length();j++){  //1 字符相等  if(str.charAt(i-1)==pattern.charAt(j-1)){      dp[i][j]=dp[i-1][j-1];  //2 j为'.'  }else if(pattern.charAt(j-1)=='.'){      dp[i][j]=dp[i-1][j-1];  //3 j为' '  }else if(pattern.charAt(j-1)==' '){      //3.1 j为' ' j-1为'.'      if(j>=2 && pattern.charAt(j-2)=='.'){   dp[i][j]=dp[i][j-2]||dp[i][j-1]||dp[i-1][j];      //3.2 j为' ' j-1不为'.'      }else{   //1 匹配成功   if(j>=2 && str.charAt(i-1)==pattern.charAt(j-2)){dp[i][j]=dp[i][j-2]||dp[i][j-1]||dp[i-1][j];   //2 匹配不成功   }else{dp[i][j]=dp[i][j-2];   }      }  }     } } return dp[str.length()][pattern.length()];    }}

BM77 最长的括号子串

描述给出一个长度为 n 的，仅包含字符 '(' 和 ')' 的字符串，计算最长的格式正确的括号子串的长度。例1: 对于字符串 "(()" 来说，最长的格式正确的子串是 "()" ，长度为 2 .例2：对于字符串 ")()())" , 来说, 最长的格式正确的子串是 "()()" ，长度为 4 .字符串长度：0≤n≤5∗10 5要求时间复杂度 O(n) ,空间复杂度 O(n).示例1输入："(()"返回值：2示例2输入："(())"返回值：4

思路：动态规划当前位置i为( dp为0当前位置i为) 需要判断1、i-1为( ,dp[i]=dp[i-2]+22、i-1不为(,i-dp[i-1]-1=='(' dp[i]=dp[i-dp[i-1]-2]+dp[i-1]+2

import java.util. ;public class Solution {    public int longestValidParentheses (String s) { int maxans = 0; int[] dp = new int[s.length()]; for (int i = 1; i < s.length(); i++) {     if (s.charAt(i) == ')') {  if (s.charAt(i - 1) == '(') {      dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;  } else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {      dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;  }  maxans = Math.max(maxans, dp[i]);     } } return maxans;    }}

BM78 打家劫舍(一)

描述你是一个经验丰富的小偷，准备偷沿街的一排房间，每个房间都存有一定的现金，为了防止被发现，你不能偷相邻的两家，即，如果偷了第一家，就不能再偷第二家；如果偷了第二家，那么就不能偷第一家和第三家。给定一个整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额。数据范围：数组长度满足1≤n≤2×10^5，数组中每个值满足1≤num[i]≤5000 示例1输入：[1,2,3,4]返回值：6说明：最优方案是偷第 2，4 个房间   示例2输入：[1,3,6]返回值：7说明：最优方案是偷第 1，3个房间   示例3输入：[2,10,5]返回值：10说明：最优方案是偷第 2 个房间

思路：动态规划每天有两种状态 偷和不偷偷 dp[i-1][1]+nums[i-1];  左边不偷+今天不偷 dp[i][1]=Math.max(dp[i-1][0],dp[i-1][1]);  昨天投和不偷的最大值

import java.util. ;public class Solution {    public int rob (int[] nums) { int[][] dp=new int[nums.length+1][2]; dp[0][0]=0; dp[0][1]=0; int max=0; for(int i=1;i<=nums.length;i++){     dp[i][0]=dp[i-1][1]+nums[i-1];     dp[i][1]=Math.max(dp[i-1][0],dp[i-1][1]);     max=Math.max(dp[i][0],dp[i][1]); } return max;    }}

BM79 打家劫舍(二)

描述你是一个经验丰富的小偷，准备偷沿湖的一排房间，每个房间都存有一定的现金，为了防止被发现，你不能偷相邻的两家，即，如果偷了第一家，就不能再偷第二家，如果偷了第二家，那么就不能偷第一家和第三家。沿湖的房间组成一个闭合的圆形，即第一个房间和最后一个房间视为相邻。给定一个长度为n的整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额。数据范围：数组长度满足1≤n≤2×10^5，数组中每个值满足1≤nums[i]≤5000 示例1输入：[1,2,3,4]返回值：6说明：最优方案是偷第 2 4 个房间      示例2输入：[1,3,6]返回值：6说明：由于 1 和 3 是相邻的，因此最优方案是偷第 3 个房间

动态规划1 从1-(n-1)2 从2-n计算两边动态规划

import java.util. ;public class Solution {    public int rob (int[] nums) { int[][] dp=new int[nums.length][2]; dp[0][0]=0; dp[0][1]=0;  int RobFirst=0; for(int i=1;i<nums.length;i++){     dp[i][0]=dp[i-1][1]+nums[i-1];     dp[i][1]=Math.max(dp[i-1][0],dp[i-1][1]);     RobFirst=Math.max(dp[i][0],dp[i][1]); }  int noRobFirst=0; dp=new int[nums.length][2]; for(int i=1;i<nums.length;i++){     dp[i][0]=dp[i-1][1]+nums[i];     dp[i][1]=Math.max(dp[i-1][0],dp[i-1][1]);     noRobFirst=Math.max(dp[i][0],dp[i][1]); } return Math.max(RobFirst,noRobFirst);    }}

BM80 买卖股票的最好时机(一)

描述假设你有一个数组prices，长度为n，其中prices[i]是股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益1.你可以买入一次股票和卖出一次股票，并非每天都可以买入或卖出一次，总共只能买入和卖出一次，且买入必须在卖出的前面的某一天2.如果不能获取到任何利润，请返回03.假设买入卖出均无手续费数据范围：0≤n≤10^5,0≤val≤10^4要求：空间复杂度 O(1)，时间复杂度 O(n)示例1输入：[8,9,2,5,4,7,1]返回值：5说明：在第3天(股票价格 = 2)的时候买入，在第6天(股票价格 = 7)的时候卖出，最大利润 = 7-2 = 5 ，不能选择在第2天买入，第3天卖出，这样就亏损7了；同时，你也不能在买入前卖出股票。     示例2输入：[2,4,1]返回值：2示例3输入：[3,2,1]返回值：0

思路：动态规划今天持有=max(今天买入,昨天就持有)今天不持有=max(昨天没有,昨天有今天卖出)

import java.util. ;public class Solution {    public int maxProfit (int[] prices) { int[][] dp=new int[prices.length][2]; dp[0][0]=0; dp[0][1]=-prices[0]; for(int i=1;i<prices.length;i++){     dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);     dp[i][1]=Math.max(dp[i - 1][1], -prices[i]); } return dp[prices.length-1][0];    }}

//暴力解法import java.util. ;public class Solution {    public int maxProfit (int[] prices) { if(prices.length<2) return 0; int max=0; for(int i=0;i<prices.length-1;i++){     int n1=prices[i];     for(int j=i+1;j<prices.length;j++){  max=Math.max(max,prices[j]-n1);     } } return max;    }}

BM81 买卖股票的最好时机(二)

描述假设你有一个数组prices，长度为n，其中prices[i]是某只股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益1. 你可以多次买卖该只股票，但是再次购买前必须卖出之前的股票2. 如果不能获取收益，请返回03. 假设买入卖出均无手续费数据范围：1≤n≤1×10^5，1≤prices[i]≤10^4要求：空间复杂度 O(n)，时间复杂度 O(n)进阶：空间复杂度 O(1)，时间复杂度 O(n)示例1输入：[8,9,2,5,4,7,1]返回值：7说明：在第1天(股票价格=8)买入，第2天(股票价格=9)卖出，获利9-8=1在第3天(股票价格=2)买入，第4天(股票价格=5)卖出，获利5-2=3在第5天(股票价格=4)买入，第6天(股票价格=7)卖出，获利7-4=3总获利1+3+3=7，返回7 示例2输入：[5,4,3,2,1]返回值：0说明：由于每天股票都在跌，因此不进行任何交易最优。最大收益为0。     示例3输入：[1,2,3,4,5]返回值：4说明：第一天买进，最后一天卖出最优。中间的当天买进当天卖出不影响最终结果。最大收益为4。  备注：总天数不大于200000。保证股票每一天的价格在[1,100]范围内。

思路：动态规划今天持有=max(昨天利润+今天买入,昨天就持有)今天不持有=max(昨天没有,昨天有今天卖出)

import java.util. ;public class Solution {    public int maxProfit (int[] prices) { int[][] dp=new int[prices.length][2]; dp[0][0]=0; dp[0][1]=-prices[0]; for(int i=1;i<prices.length;i++){     dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);     dp[i][1]=Math.max(dp[i - 1][1],dp[i-1][0] -prices[i]); } return dp[prices.length-1][0];    }}

BM82 买卖股票的最好时机(三)

描述假设你有一个数组prices，长度为n，其中prices[i]是某只股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益1. 你最多可以对该股票有两笔交易操作，一笔交易代表着一次买入与一次卖出，但是再次购买前必须卖出之前的股票2. 如果不能获取收益，请返回03. 假设买入卖出均无手续费数据范围：1≤n≤10^5，股票的价格满足1≤val≤10^4要求: 空间复杂度 O(n)，时间复杂度 O(n)进阶：空间复杂度 O(1)，时间复杂度 O(n)示例1输入：[8,9,3,5,1,3]返回值：4说明：第三天(股票价格=3)买进，第四天(股票价格=5)卖出，收益为2第五天(股票价格=1)买进，第六天(股票价格=3)卖出，收益为2总收益为4。示例2输入：[9,8,4,1]返回值：0示例3输入：[1,2,8,3,8]返回值：12说明：第一笔股票交易在第一天买进，第三天卖出；第二笔股票交易在第四天买进，第五天卖出；总收益为12。因最多只可以同时持有一只股票，所以不能在第一天进行第一笔股票交易的买进操作，又在第二天进行第二笔股票交易的买进操作（此时第一笔股票交易还没卖出），最后两笔股票交易同时在第三天卖出，也即以上操作不满足题目要求。 备注：总天数不大于200000。保证股票每一天的价格在[1,100]范围内。

思路：5个状态：1）不操作2）第一次购买3）第一次卖出4）第二次购买5）第二次卖出

import java.util. ;public class Solution {    public int maxProfit (int[] prices) { // write code here if (prices.length == 0) return 0; /  5个状态：1）不操作2）第一次购买3）第一次卖出4）第二次购买5）第二次卖出 dp[i][j]代表第i天状态为j时产生的最大收益  / int [][]dp = new int[prices.length][5]; //初始化 dp[0][1] = -prices[0]; dp[0][3] = -prices[0]; for (int i = 1; i<prices.length; i++) {     dp[i][0] = dp[i - 1][0];     //其中dp[i][1]有两个操作1）第i天没有操作2）第i天买入股票，所以此时最大收益，应该为这两个操作比大小     dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);     //其中dp[i][2]有两个操作1）第i天没有操作2）第i天卖出股票，所以此时最大收益，应该为这两个操作比大小     dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);     //其中dp[i][3]有两个操作1）第i天没有操作2）第i天买入股票，所以此时最大收益，应该为这两个操作比大小     dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);     //其中dp[i][4]有两个操作1）第i天没有操作2）第i天卖出股票，所以此时最大收益，应该为这两个操作比大小     dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]); } return dp[prices.length - 1][4];    }}

英语听力