第十三届蓝桥杯大赛软件赛省赛C/C++大学B组题目及部分答案

本文章的答案仅供参考，太菜了，没做完

一.填空题（2道）

试题 A: 九进制转十进制

本题总分： 5 分
【问题描述】
九进制正整数 (2022) 9 转换成十进制等于多少？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案：1478

试题 B: 顺子日期
本题总分：5 分
【问题描述】
小明特别喜欢顺子。顺子指的就是连续的三个数字：123、456 等。顺子日
期指的就是在日期的 yyyymmdd 表示法中，存在任意连续的三位数是一个顺
子的日期。例如 20220123 就是一个顺子日期，因为它出现了一个顺子：123；
而 20221023 则不是一个顺子日期，它一个顺子也没有。小明想知道在整个 2022
年份中，一共有多少个顺子日期。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
答案：6

---

二：编程题（8道）
试题 C: 刷题统计
时间限制: 1.0s 内存限制: 256.0MB 本题总分：10 分
【问题描述】
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天
做 a 道题目，周六和周日每天做 b 道题目。请你帮小明计算，按照计划他将在
第几天实现做题数大于等于 n 题？
【输入格式】
输入一行包含三个整数 a, b 和 n.
【输出格式】
输出一个整数代表天数。
【样例输入】
10 20 99
【样例输出】
8
【评测用例规模与约定】
对于 50% 的评测用例，1 ≤ a,b,n ≤ 10 6 .
对于 100% 的评测用例，1 ≤ a,b,n ≤ 10 18 .

#include#define N 1e18int main(){long long sum=0;long long a,b,n;scanf("%lld%lld%lld",&a,&b,&n);for(long long i=1;i=n){printf("%lld",i);break;}}return 0;}

试题 D: 修剪灌木
时间限制: 1.0s 内存限制: 256.0MB 本题总分：10 分
【问题描述】
爱丽丝要完成一项修剪灌木的工作。
有 N 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晚会修剪一棵灌
木，让灌木的高度变为 0 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始，
每天向右修剪一棵灌木。当修剪了最右侧的灌木后，她会调转方向，下一天开
始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。
灌木每天从早上到傍晚会长高 1 厘米，而其余时间不会长高。在第一天的
早晨，所有灌木的高度都是 0 厘米。爱丽丝想知道每棵灌木最高长到多高。
【输入格式】
一个正整数 N ，含义如题面所述。
【输出格式】
输出 N 行，每行一个整数，第行表示从左到右第 i 棵树最高能长到多高。
【样例输入】
3
【样例输出】
4
2
4
【评测用例规模与约定】
对于 30% 的数据，N ≤ 10.
对于 100% 的数据，1 < N ≤ 10000.

代码：

#includeint main(){int n,i,j,k;scanf("%d",&n);int a[n];int b[n];for(i=0;i<n;i++){a[i]=0;b[i]=0; }for(i=1;i<=10;i++){if(i%2==1){for(j=0;j<n;j++){a[j]=0;for(k=0;kb[k]){b[k]=a[k];}}}}else{for(j=n-1;j>=0;j--){a[j]=0;for(k=n-1;k>=0;k--){if(k!=j){a[k]+=1;}if(a[k]>b[k]){b[k]=a[k];}}}}}for(i=0;i<n;i++){printf("%d\n",b[i]); }return 0;}

试题 E: X 进制减法
时间限制: 1.0s 内存限制: 256.0MB 本题总分：15 分
【问题描述】
进制规定了数字在数位上逢几进一。
X 进制是一种很神奇的进制，因为其每一数位的进制并不固定！例如说某
种 X 进制数，最低数位为二进制，第二数位为十进制，第三数位为八进制，则
X 进制数 321 转换为十进制数为 65。
现在有两个 X 进制表示的整数 A 和 B，但是其具体每一数位的进制还不确
定，只知道 A 和 B 是同一进制规则，且每一数位最高为 N 进制，最低为二进
制。请你算出 A − B 的结果最小可能是多少。
请注意，你需要保证 A 和 B 在 X 进制下都是合法的，即每一数位上的数
字要小于其进制。
【输入格式】
第一行一个正整数 N，含义如题面所述。
第二行一个正整数 M a ，表示 X 进制数 A 的位数。
第三行 M a 个用空格分开的整数，表示 X 进制数 A 按从高位到低位顺序各
个数位上的数字在十进制下的表示。
第四行一个正整数 M b ，表示 X 进制数 B 的位数。
第五行 M b 个用空格分开的整数，表示 X 进制数 B 按从高位到低位顺序各
个数位上的数字在十进制下的表示。
请注意，输入中的所有数字都是十进制的。
【输出格式】
输出一行一个整数，表示 X 进制数 A − B 的结果的最小可能值转换为十进
制后再模 1000000007 的结果。

【样例输入】
11
3
10 4 0
3
1 2 0
【样例输出】
94
【样例说明】
当进制为：最低位 2 进制，第二数位 5 进制，第三数位 11 进制时，减法
得到的差最小。此时 A 在十进制下是 108，B 在十进制下是 14，差值是 94。
【评测用例规模与约定】
对于 30% 的数据，N ≤ 10; M a , M b ≤ 8.
对于 100% 的数据，2 ≤ N ≤ 1000;1 ≤ M a , M b ≤ 100000;A ≥ B.

这题：原谅我看不懂题目，求大神教我

试题 F: 统计子矩阵
时间限制: 1.0s 内存限制: 256.0MB 本题总分：15 分
【问题描述】
给定一个 N × M 的矩阵 A，请你统计有多少个子矩阵 (最小 1 × 1，最大
N × M) 满足子矩阵中所有数的和不超过给定的整数 K?
【输入格式】
第一行包含三个整数 N, M 和 K.
之后 N 行每行包含 M 个整数，代表矩阵 A.
【输出格式】
一个整数代表答案。
【样例输入】
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
【样例输出】
19
【样例说明】
满足条件的子矩阵一共有 19，包含：
大小为 1 × 1 的有 10 个。
大小为 1 × 2 的有 3 个。
大小为 1 × 3 的有 2 个。
大小为 1 × 4 的有 1 个。
大小为 2 × 1 的有 3 个。
【评测用例规模与约定】
对于 30% 的数据，N, M ≤ 20.
对于 70% 的数据，N, M ≤ 100.
对于 100% 的数据，1 ≤ N, M ≤ 500;0 ≤ A ij ≤ 1000;1 ≤ K ≤ 250000000.

我打不出来代码：反正就是很多循环

试题 G: 积木画
时间限制: 1.0s 内存限制: 256.0MB 本题总分：20 分
【问题描述】
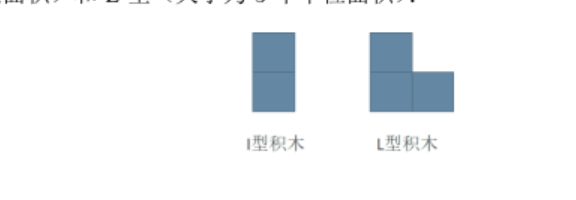
小明最近迷上了积木画，有这么两种类型的积木，分别为 I 型（大小为 2
个单位面积）和 L 型（大小为 3 个单位面积）：

同时，小明有一块面积大小为 2 × N 的画布，画布由 2 × N 个 1 × 1 区域构
成。小明需要用以上两种积木将画布拼满，他想知道总共有多少种不同的方式？
积木可以任意旋转，且画布的方向固定。
【输入格式】
输入一个整数 N，表示画布大小。
【输出格式】
输出一个整数表示答案。由于答案可能很大，所以输出其对 1000000007 取
模后的值
【样例输入】
3
【样例输出】
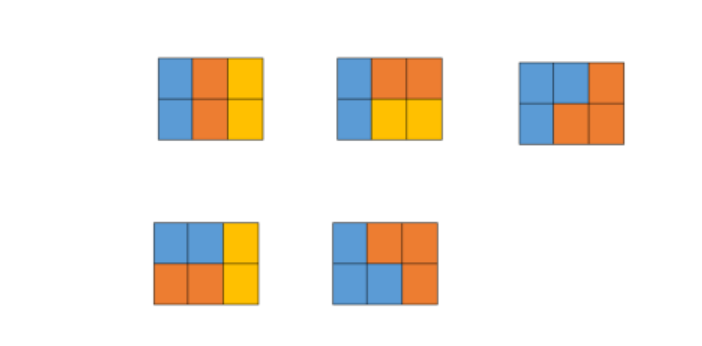
5

【样例说明】
五种情况如下图所示，颜色只是为了标识不同的积木：

 

【评测用例规模与约定】
对于所有测试用例，1 ≤ N ≤ 10000000.

 

这题我也没做出来，猜是用递归

H扫雷

时间限制: 1.0s 内存限制: 256.0MB 本题总分：20 分
【问题描述】
小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下，
在一个二维平面上放置着 n 个炸雷，第 i 个炸雷 (x i ,y i ,r i ) 表示在坐标 (x i ,y i ) 处
存在一个炸雷，它的爆炸范围是以半径为 r i 的一个圆。
为了顺利通过这片土地，需要玩家进行排雷。玩家可以发射 m 个排雷火
箭，小明已经规划好了每个排雷火箭的发射方向，第 j 个排雷火箭 (x j ,y j ,r j ) 表
示这个排雷火箭将会在 (x j ,y j ) 处爆炸，它的爆炸范围是以半径为 r j 的一个圆，
在其爆炸范围内的炸雷会被引爆。同时，当炸雷被引爆时，在其爆炸范围内的
炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷？
你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个
炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
【输入格式】
输入的第一行包含两个整数 n、m.
接下来的 n 行，每行三个整数 xi ,yi ,ri ，表示一个炸雷的信息。
再接下来的 m 行，每行三个整数 xj ,yj ,rj ，表示一个排雷火箭的信息。
【输出格式】
输出一个整数表示答案。
【样例输入】
2 1
2 2 4
4 4 2
0 0 5
【样例输出】
2
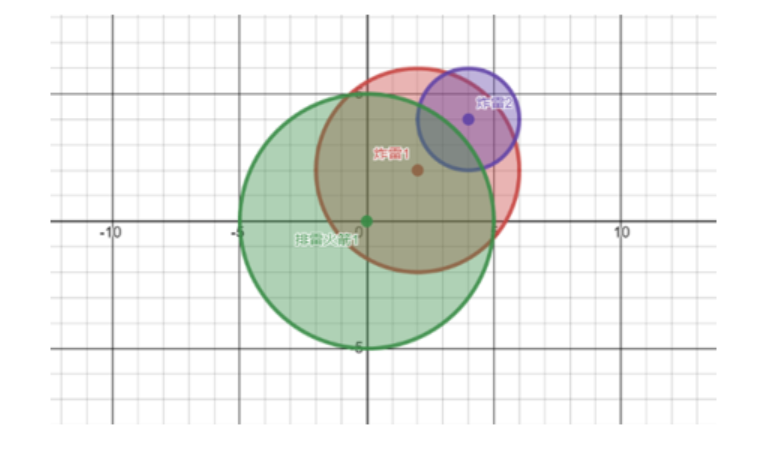
【样例说明】
示例图如下，排雷火箭 1 覆盖了炸雷 1，所以炸雷 1 被排除；炸雷 1 又覆
盖了炸雷 2，所以炸雷 2 也被排除。

 

【评测用例规模与约定】
对于 40% 的评测用例：0 ≤ x,y ≤ 10 9 ,0 ≤ n,m ≤ 10 3 ,1 ≤ r ≤ 10.
对于 100% 的评测用例：0 ≤ x,y ≤ 10 9 ,0 ≤ n,m ≤ 5 × 10 4 ,1 ≤ r ≤ 10.

#includeint main(){int n,m,i,j;float l;scanf("%d%d",&n,&m);float a[n][3];int c[n];for(i=0;i<n;i++){c[i]=0;scanf("%f%f%f",&a[i][0],&a[i][1],&a[i][2]);}float b[m][3];for(i=0;i<m;i++){scanf("%f%f%f",&b[i][0],&b[i][1],&b[i][2]);}for(i=0;i<n;i++){for(j=0;j<m;j++){l=(a[i][0]-b[j][0])*(a[i][0]-b[j][0])*1.0+(a[i][1]-b[j][1])*(a[i][1]-b[j][1])*1.0;if(l<(b[j][2]*b[j][2])){c[i]=1;}}}for(i=0;i<n-1;i++){for(j=i+1;j<n;j++){if(c[i]==1){l=(a[i][0]-a[j][0])*(a[i][0]-a[j][0])+(a[i][1]-a[j][1])*(a[i][1]-a[j][1]);if(l<a[i][2]*a[i][2]) {c[j]=1;}}}}int sum=0;for(i=0;i<n;i++){if(c[i]==1){sum++;}}printf("%d",sum);return 0;}

试题 I: 李白打酒加强版
时间限制: 1.0s 内存限制: 256.0MB 本题总分：25 分
【问题描述】
话说大诗人李白，一生好饮。幸好他从不开车。
一天，他提着酒壶，从家里出来，酒壶中有酒 2 斗。他边走边唱：
无事街上走，提壶去打酒。
逢店加一倍，遇花喝一斗。
这一路上，他一共遇到店 N 次，遇到花 M 次。已知最后一次遇到的是花，
他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序，有多少种不同的可能？
注意：壶里没酒 ( 0 斗) 时遇店是合法的，加倍后还是没酒；但是没酒时遇
花是不合法的。
【输入格式】
第一行包含两个整数 N 和 M.
【输出格式】
输出一个整数表示答案。由于答案可能很大，输出模 1000000007 的结果。
【样例输入】
5 10
【样例输出】
14
【样例说明】
如果我们用 0 代表遇到花，1 代表遇到店，14 种顺序如下：

010101101000000
010110010010000
011000110010000
100010110010000
011001000110000
100011000110000
100100010110000
010110100000100
011001001000100
100011001000100
100100011000100
011010000010100
100100100010100
101000001010100
【评测用例规模与约定】
对于 40% 的评测用例：1 ≤ N, M ≤ 10。
对于 100% 的评测用例：1 ≤ N, M ≤ 100

 

原谅我不配做后面的题目

J砍竹子

本题总分：25 分
【问题描述】

这天，小明在砍竹子，他面前有 n 棵竹子排成一排，一开始第 i 棵竹子的
高度为 h i .
他觉得一棵一棵砍太慢了，决定使用魔法来砍竹子。魔法可以对连续的一
段相同高度的竹子使用，假设这一段竹子的高度为 H，那么使用一次魔法可以
把这一段竹子的高度都变为 
，其中 ⌊x⌋ 表示对 x 向下取整。小明想
知道他最少使用多少次魔法可以让所有的竹子的高度都变为 1。
【输入格式】
第一行为一个正整数 n，表示竹子的棵数。
第二行共 n 个空格分开的正整数 h i ，表示每棵竹子的高度。
【输出格式】
一个整数表示答案。
【样例输入】
6
2 1 4 2 6 7
【样例输出】
5
【样例说明】
其中一种方案：
2 1 4 2 6 7

 

试题 J: 砍竹子 16

→ 2 1 4 2 6 2
→ 2 1 4 2 2 2
→ 2 1 1 2 2 2
→ 1 1 1 2 2 2
→ 1 1 1 1 1 1
共需要 5 步完成
【评测用例规模与约定】
对于 20% 的数据，保证 n ≤ 1000,h i ≤ 10 6 。
对于 100% 的数据，保证 n ≤ 2 × 10 5 ,h i ≤ 10 18 。
 

我不配做这题