文章目录

• 136. 只出现一次的数字
• 137. 只出现一次的数字 II
• 260. 只出现一次的数字 III

136. 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1

示例 2:

输入: [4,1,2,1,2]
输出: 4

通过位运算，我们知道：

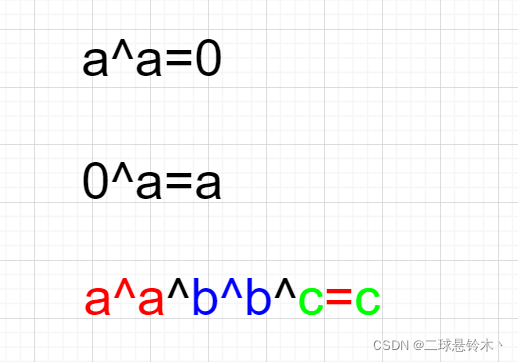
思路：
基于异或的性质，
我们可以直接将全部元素异或。
这样的话，结果就是0异或x，就得出了x的值。

int singleNumber(int* nums, int numsSize){    int ret = 0;    for(int i = 0;i<numsSize;i++)    { ret^=nums[i];    }    return ret;}

137. 只出现一次的数字 II

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

示例 1：

输入：nums = [2,2,3,2]
输出：3

示例 2：

输入：nums = [0,1,0,1,0,1,99]
输出：99

思路：
如果我们在每个二进制位上进行加减，
由于其他数字都是3个，对他们的和取余为0.

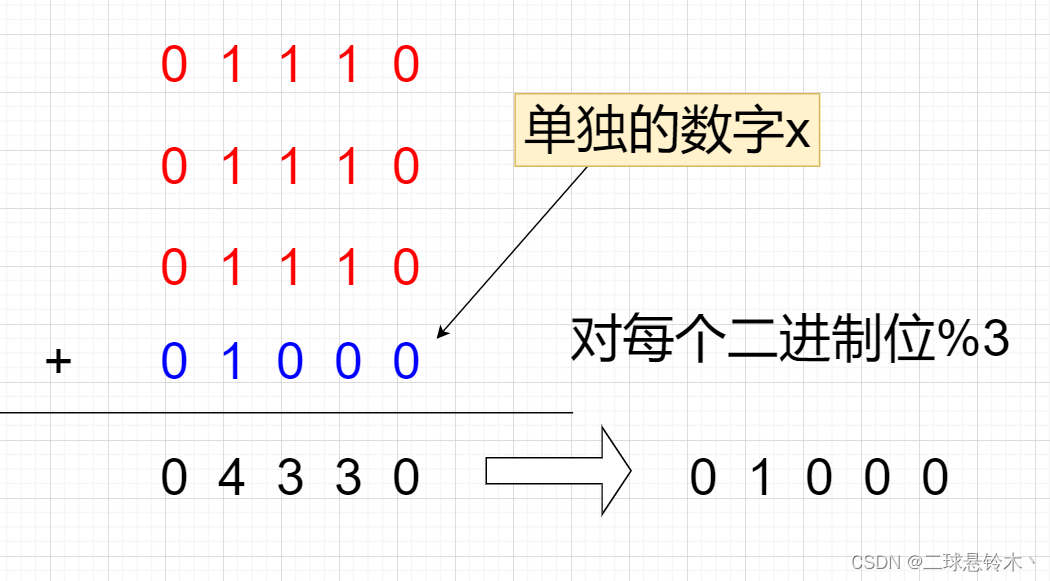
这样的话我们可以得出单独的数x的每一个二进制位，
利用左移即可求出x。

int singleNumber(int* nums, int numsSize){int i = 0;int j = 0;int sum = 0;for(i = 0;i<32;i++){    size_t count = 0;    for(j=0;j<numsSize;j++)    { count+=(nums[j]>>i)&1;    }    sum+=(count%3)<<i;}return sum;}

260. 只出现一次的数字 III

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

进阶：你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

示例 1：

输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案。

示例 2：

输入：nums = [-1,0]
输出：[-1,0]

示例 3：

输入：nums = [0,1]
输出：[1,0]

思路：
得到上一题的启示，我们是不是还可以用位运算来解题呢？
如果数组是由很多组一对数字和一个单独的数字x组成，
我们仍可以全部异或。
但是本题是两个单独的数字，
我们自然想到了将这群数字分成两组，然后使用异或。

在所有元素中，取二进制第x位为1的元素全部异或，就可以得出一个单独的数字x。

由于一开始就得出了所有元素异或的结果x异或y，
现在又有了x，自然可以求出y。
代码如下：

int* singleNumber(int* nums, int numsSize, int* returnSize){所有元素异或    int ret = 0;    for(int i = 0;i < numsSize;i++)    { ret^=nums[i];    }    寻找二进制位中的1，下标存入pos    int pos = 0;    for(int i = 0;i < 32;i++)    { if((ret>>i)&1==1) {     pos = i;     break; }    }    int single_1=0;    int single_2=0;    分组，求single_1    for(int i = 0;i < numsSize;i++)    { if((nums[i]>>pos)&1==1) {     single_1^=nums[i]; }    }//利用single_1和ret求出single_2    single_2=single_1^ret;    *returnSize=2;     int *ans=malloc(sizeof(int)*2);     ans[0]=single_1;     ans[1]=single_2;     return ans;}

• 时间复杂度：O(n)。
• 空间复杂度：O(1)。

图解：

int ret = 0;    for(int i = 0;i < numsSize;i++)    { ret^=nums[i];    }    int pos = 0;    for(int i = 0;i < 32;i++)    { if((ret>>i)&1==1) {     pos = i;     break; }    }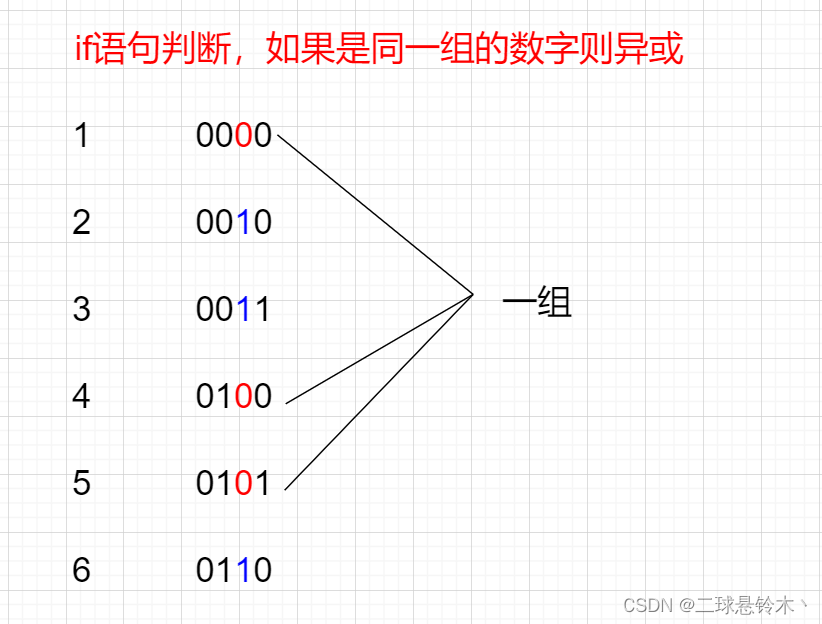

int single_1=0;    int single_2=0;    for(int i = 0;i < numsSize;i++)    { if((nums[i]>>pos)&1==1) {     single_1^=nums[i]; }    }    single_2=single_1^ret;

以上就是今天位运算的全部内容了。

全民K歌