二叉树实现堆
利用二叉树实现堆
-
-
- 1. 堆的定义
- 2. 如何利用二叉树实现堆
- 性质
- ==堆的实现==:
-
- 以上是实现过程中自己实现的排序和交换代码。分开更容易理解。
- 总结:
-
1. 堆的定义
2. 如何利用二叉树实现堆
堆的定义:如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: <= 且 = 且 >= ) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
性质
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树。
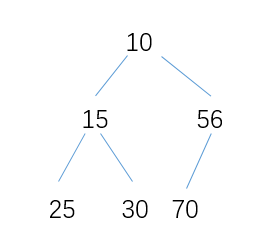
小堆如图如下
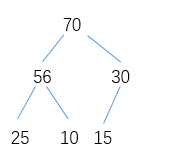
大堆如图如下
堆的实现:
这个视频模拟了插入中小堆的实现,如何移动的过程。
小堆
定义结构体
typedef int HPDatatype;typedef struct Heap{HPDatatype* a;size_t size;size_t capacity;}Hp;```c//堆排序代码void AdjustUp(HPDatatype* a, size_t child){//小的在上的排序法size_t parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]); child = parent;parent = (child - 1) / 2;}else{break;}}}//堆内元素交换代码void Swap(HPDatatype* pa, HPDatatype* phh){HPDatatype tmp = *pa;*pa = *phh;*phh = tmp;}以上是实现过程中自己实现的排序和交换代码。分开更容易理解。
| 堆 | 函数名 |
|---|---|
| 初始化堆 | void HeapInit(Hp* hpp) |
| 堆的销毁 | void HeapDestroy(Hp* hpp) |
| 堆的插入 | void HeapPush(Hp* hpp, HPDatatype x) |
| 堆的打印 | void HeapPrint(Hp* hpp) |
| 堆的删除 | void HeapPop(Hp* hpp) |
| 堆的判空 | bool HeapEmpty(Hp* phh) |
| 堆的深度 | size_t HeapSize(Hp* phh) |
1.堆的初始化:
我们将创建的结构体里面的数组置为空处理。在将容量和长度初始化为0。
下面展示一些 内联代码片。
void HeapInit(Hp* hpp){assert(hpp);hpp->a = NULL;hpp->size = hpp->capacity = 0;}**2.**对我们的堆进行销毁:我们释放数组里面的数据。在将a置为空,在将容量和长度初始化为0。这步和初始化一样。```cvoid HeapDestroy(Hp* hpp){assert(hpp);free(hpp->a);hpp->a = NULL;hpp->size = hpp->capacity = 0;}3.堆的插入:
这步比较特殊里面有内存开辟先判断空间是否存在,如果不存在就开辟空间。开辟完后将值放入结构体数组里面,我们创建个函数进行堆排序函数名为void AdjustUp(HPDatatype* a, size_t child)在这个函数里面又有Swap函数是一个交换函数具体使用就是将头和尾进行交换代码如下:

//插入void HeapPush(Hp* hpp, HPDatatype x){assert(hpp);if (hpp->size == hpp->capacity){size_t newCapacity = hpp->capacity == 0 ? 4 : hpp->capacity * 2;HPDatatype* tmp = realloc(hpp->a,sizeof(HPDatatype)* newCapacity);if (tmp == NULL){printf("realloc failed\n");exit(-1);}hpp->a = tmp;hpp->capacity = newCapacity;}hpp->a[hpp->size] = x;++hpp->size;//大/小堆排序AdjustUp(hpp->a, hpp->size-1);}4.堆的删除:
我们对堆进行断言,使堆中有数据存在。
我们将堆首和堆尾元素进行交换,在使size–这样就将我们删除的元素给删除了。删除完在进行排序继续使用AdjustDown函数进行堆排序
void HeapPop(Hp* hpp){assert(hpp);assert(hpp->size > 0);Swap(&hpp->a[0], &hpp->a[hpp->size-1]);--hpp->size;AdjustDowm(hpp->a, hpp->size, 0);}5.堆的判空:
这边使用的是c++里面bool,如有需要自己查。
bool HeapEmpty(Hp* hpp){assert(hpp);return hpp->size == 0;}6.堆的深度:
直接将结构体中size取出即为深度。
size_t HeapSize(Hp* hpp){assert(hpp);return hpp->size;}总结:
学习使我强大。我要变强


