聚类分析，听起来高大上，其实就是一种“物以类聚”的技术。它通过数据的特征，把相似的点归为一类，不同的点分开来。就像你把朋友圈里的人分成“吃货”、“健身狂”、“加班狗”一样，聚类分析也能帮你快速分类，只是它更“硬核”——用数学和数据说话。

问题来了：聚类分析的核心是什么？答案很明显——距离。无论是欧几里得距离还是余弦相似度，距离决定了谁和谁更“亲近”。但在实际应用中，选择哪种距离计算方法往往让人头疼。比如，如果数据维度很高，欧几里得距离可能会失效，这时候余弦相似度可能更靠谱。

再深入一点，聚类分析的应用场景非常广泛。从市场细分到社交网络分析，再到生物信息学，聚类分析都能大显身手。但要注意的是，聚类结果的好坏不仅仅取决于算法，数据预处理和特征选择同样关键。就像你去参加饭局，先得知道自己想吃什么，才能决定去哪家餐厅。

最后，聚类分析并不是万能的。它只能帮你发现数据中的潜在模式，但无法告诉你这些模式背后的原因。因此，结合领域知识和后续分析，才能让聚类分析的价值最大化。就像你发现朋友圈里有一群“夜猫子”，但你得进一步分析他们是熬夜加班还是刷剧追番，才能得出有意义的结论。

目录

聚类分析的定义及原理

聚类方法及其在SPSS中的实现

总结及拓展

聚类分析的定义及原理

1.定义

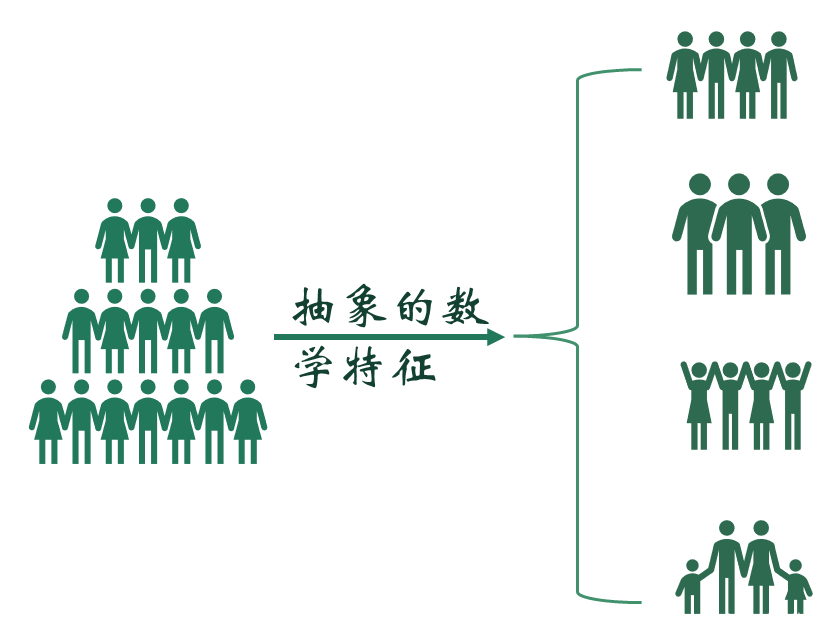
       所谓物以类聚、人以群分。聚类分析，即是基于研究对象的特征，将他们分门别类，以让同类别的个体之间差异相对小、相似度相对大，不同类别之间的个体差异大、相似度小。

       聚类分析是一种探索性分析方法，与判别分析不同，聚类分析事先并不知道分类的标准，甚至不知道应该分成几类，而是会根据样本数据的特征，自动进行分类。

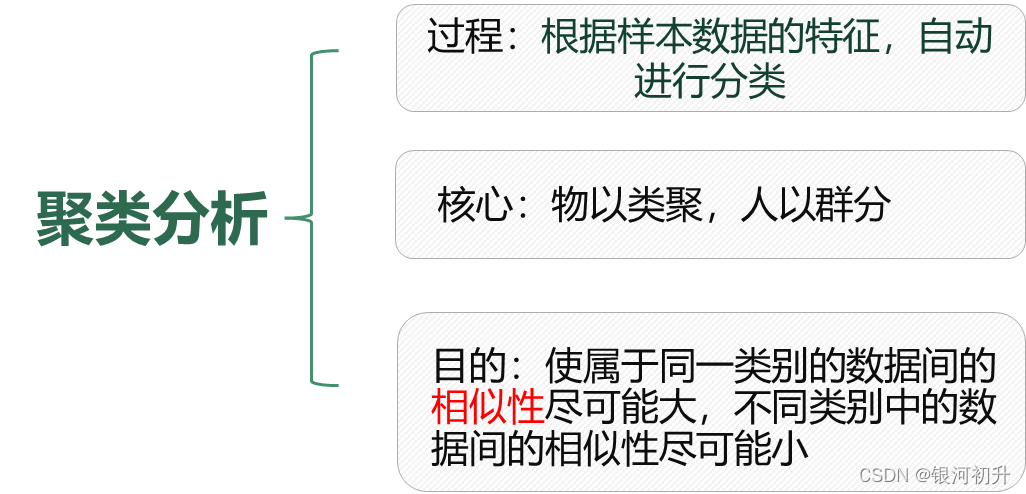
          聚类与分类的不同在于，聚类所要求划分的类是未知的

 2.原理

        假定研究对象均用所谓的“点”来表示。
        在聚类分析中，一般的规则是将“距离”较小的点归为同一类，将“距离”较大的点归为不同的类。
常见的是对个案分类，也可以对变量分类，但对于变量分类此时一般使用相似系数作为“距离”测量指标。

       一般的规则：

聚类方法及其在SPSS中的实现

1.主要的聚类方法：

 2.方法详解：

（1）：K-means聚类

        又称为快速聚类（K-Means Cluster），是在聚类的类别数已确定的情况下，快速将其他个案归类到相应的类别，适合大样本数据的聚类。

        具体步骤如下：

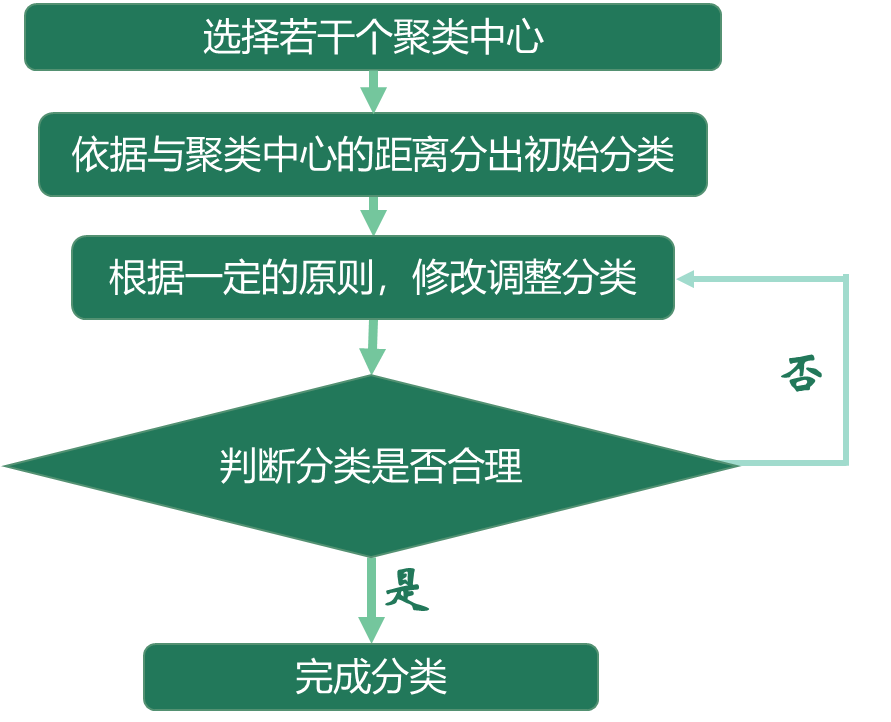
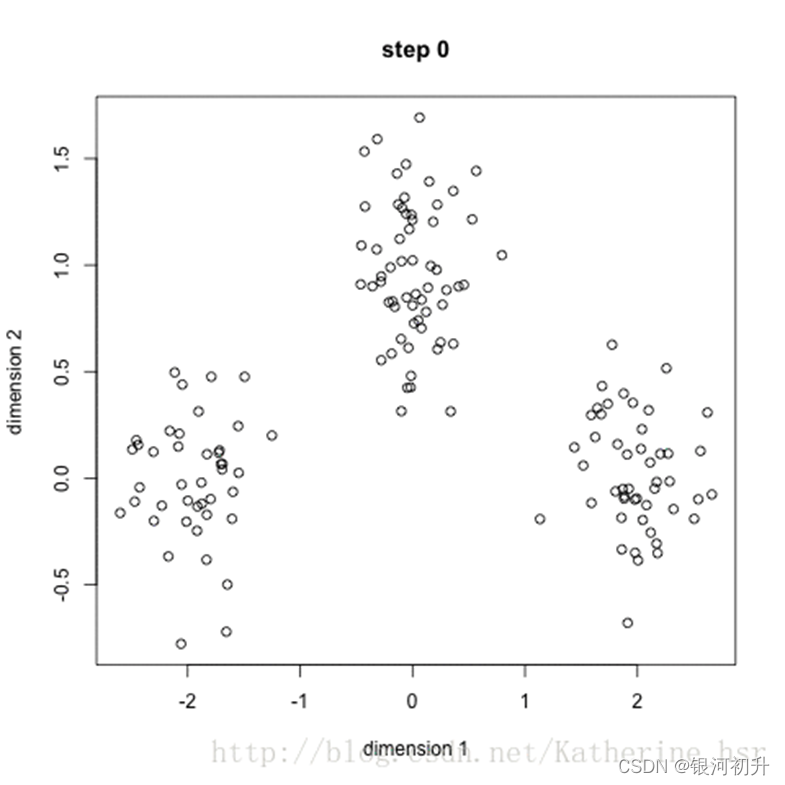
         距离计算规则（欧几你得距离公式）：
 

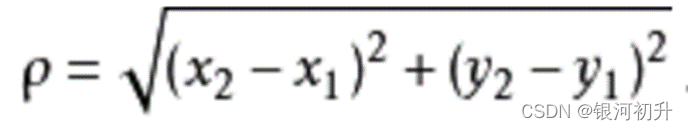
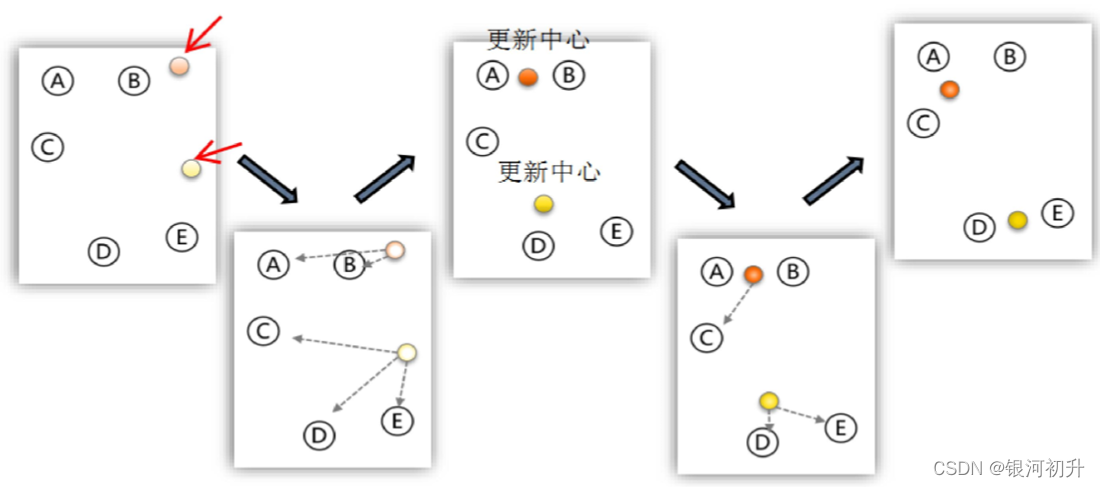
         图解：

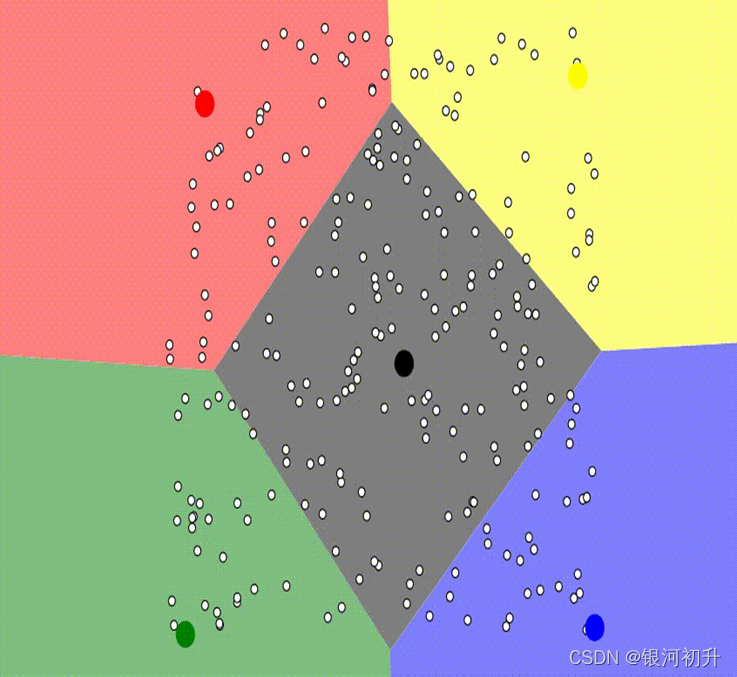
K-means的优缺点：

优势：

（1）原理比较简单，实现也很容易，收敛速度快。

（2）在对大规模数据集进行聚类分析时，算法聚类较高效且聚类效果较好。

（3）簇与簇之间区别明显时，它的聚类效果很好。

不足：

（1）分类数从初始分类开始就确定不变了，所以要求事先要对样本有足够的了解。

（2）仅限于个案间的聚类（Q型聚类），不能对变量进行聚类。

（3）个案间的距离的测量方法使用的是欧式距离的平方，因此只能对连续变量进行聚类。

案例分析（SPSS）：
通过查询整理出了2018年我国各省份的20项基本情况，根据这些指标把这31个省市或地区分成3类。

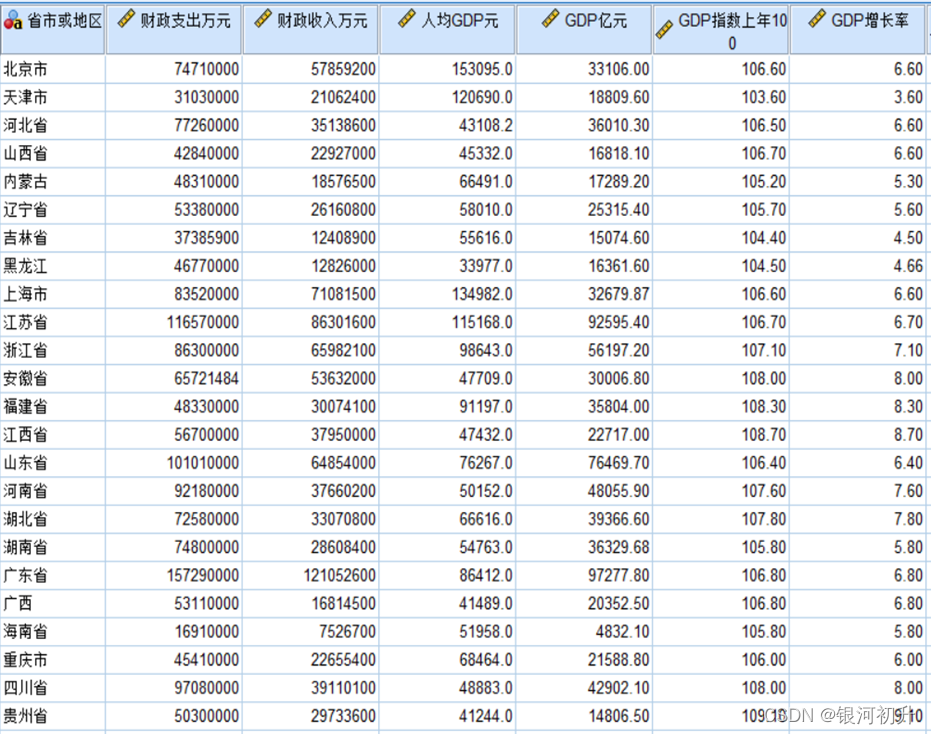
 分析步骤：分析>>分类>>K-均值聚类>>迭代>>次数>>选项>>勾选统计>>确认