网站导航
> 文档中心 > python算法思维笔记(1)

python算法思维笔记(1)

网友: 文档中心 2022-05-09 16:03:44

文章目录

    • 常见时间复杂度
      • 线性时间
        • 斐波那契数列
    • 迭代法
      • 辗转相除法求最大公约数问题
    • 穷举法
      • 找出质量之和为X的组合
      • 计算最短路径
    • 二分法
      • 搜素算法
        • 线性查找：O(n)，不需要排序
        • 二分查找：O(log2^n)，需要先排序
      • 二分法的核心：每次都将解的搜索空间大小缩小为原先的一半
      • 查找数字和
      • 求方程的根
      • 求和问题
      • 棍子的膨胀

常见时间复杂度

时间复杂度 说明 举例
O(1) 常数 217
O(logn) 对数 4logn+12
O(n) 线性 3n+21
O(nlogn) 对数线性 2n+3nlogn+15
O(n2) 平方 6n2+5n+19
O(n3) 立方 2n3+3n2+5n+8
O(2n) 指数 7*3n

算法思维：解决复杂问题
衡量标准：问题的规模n
讨论的问题：当n->∞，问题能不能得到解决
算法解决的问题：当n非常大时，
普通程序不能工作：
占用空间太大了，运行时间太长了
怎么办？
需要优化算法：提出、评估满足大规模问题的优化算法

线性时间

斐波那契数列

n = 100  # 问题规模result = [1, 2]while len(result) < 100:    x = result[-1] + result[-2]  # 计算下一个值    result.append(x)  # 将新值放入列表print(result)# 程序需要运行3+3*(n-2)，它的时间复杂度是O(n)，线性时间'''假定以行为单位，计算运行时间(1)(2)(3):3(3)(4)(5):循环n-2遍，每一遍运行3行，3*(n-2)'''# 总运行时间T(n)=3+3*(n-2)=O(n)# 空间复杂度S(n)=n+2=O(n)# 改进:降低空间复杂度n = 100x, y = 1, 2for i in range(n - 2):    x, y = y, x + yprint(y)# 总运行时间T(n)=3+2*(n-2)=O(n)# 空间复杂度S(n)=4=O(1)

迭代法

迭代法是从某个值开始，不断地利用旧值推导出新值的算法。
通常通过一个循环，不断地用某种方法从旧值产生新值。
循环到某个条件满足时，可以得到最终解。

辗转相除法求最大公约数问题

在这里插入图片描述

a, b = eval(input())if a < b: a, b = b, awhile b != 0:    a, b = b, a % b  # 利用旧值推导新值 最后b=0，a为最大公约数print(a)# 由于每两次迭代后余数最多为原来的一半，最多需要迭代2logb次，因此时间复杂度为O(logb)

穷举法

穷举法也叫暴力法，如果在问题求解时，无法找到有效的解决问题的办法，可以对所有可能的解进行逐一验证，将符合要求的解找出来。

找出质量之和为X的组合

对前面n-1个数进行循环（外循环），每次外循环，都将这个数和它后面的所有数依次进行配对（内循环）。
找出质量之和为X的组合

def find(A, X):    for i in range(len(A) - 1): for j in range(i + 1, len(A)):     if A[i] + A[j] == X:  return i, j    return -1, -1A = [18, 9, 25, 6, 19, 14, 8, 27, 15]X = 22i, j = find(A, X)if i != -1:    print(A[i], A[j])else:    print("没有可行解")

计算最短路径

根据排列组合，一共有432=24种不同的方法可供选择。
依据穷举法，可将这24种方法全部计算出来，然后输出最短的距离即可。

def get_dis(p1, p2):    return ((p2[0] - p1[0]) ** 2 + (p2[1] - p1[1]) ** 2) ** 0.5A = ((100, 50), (200, 25), (50, 30), (150, 10))min_dis = 1e10for x1, y1 in A:    for x2, y2 in A: if (x2, y2) == (x1, y1):     continue for x3, y3 in A:     if (x3, y3) in ((x1, y1), (x2, y2)):  continue     for x4, y4 in A:  if (x4, y4) in ((x1, y1), (x2, y2), (x3, y3)):      continue  dis = get_dis((0, 0), (x1, y1)) + get_dis((x1, y1), (x2, y2)) + get_dis((x2, y2), (x3, y3)) + get_dis(      (x3, y3), (x4, y4)) + get_dis((x4, y4), (0, 0))  if dis < min_dis:      min_dis = disprint('{:.2f}'.format(min_dis))

二分法

搜素算法

线性查找：O(n)，不需要排序

def search(A, x):    for i in range(len(A)):#下标循环 if x == A[i]:     return i    return -1  # 没找到返回-1def search(A, x):    for i,a in enumerate(A):#下标和元素混合循环 if x == a:     return i    return -1  # 没找到返回-1A = [52, 49, 6, 24, 19, 60, 134, 88]idx = search(A, 19)print(idx)idx = A.index(19)  # 列表的index都是1阶print(idx)

二分查找：O(log2^n)，需要先排序

使用二分法进行搜索是经典的搜索算法，指的是在一个已经排序的序列中，查找指定的值，若找到，返回索引。
二分搜索可以极大的提高查找效率，其时间复杂度是O(logn)，当然，它要求序列是已经排好序的。

排序算法：快速排序：O(nlog2^n)
二分查找的最终复杂度：O(nlog2^n)
比线性查找还差！？
二分查找适合于：排序少，查找多的场合

n次查找n个元素序列
线性查找，O(n)*n=O(n^2)
如果n个元素保持不变，排序只需要排1次，O(nlog2^n)
用二分查找总的时间复杂度O(nlog2^n)

搜索引擎，查找速度特别快
虽然网页特别多，比如2^64个网页
事先被排序，真正的查找只有64步
在巨型计算机只要0.XXX秒

二分法的核心：每次都将解的搜索空间大小缩小为原先的一半

二分查找需要排序，python的list已带有排序函数，采用的是快速排序法，时间复杂度为O(nlogn)。

A=[34,6,19,14,20,4,88]A.sort()  #从小到大排序A.sort(reverse=True)  #重大到小排序

二分查找的基本思想：

  1. 在列表A的区间 [i,j] (i<=j)中查找x，其中i,j为索引。
  2. 考察区间中间的元素的值，y=A[(i+j)//2]，若x==y，算法结束；若xy，则x必定位于原区间的右半边，即[(i+j)//2+1,j]。
  3. 在新的区间（原区间一半大小）中继续查找。
  4. 重复2、3的步骤，区间不断缩小直到找到。
  5. 若直到区间无效时(i>j)，还没找到x，则x不在A中。
def binary_search(A, x):#从A里面找x    i, j = 0, len(A) - 1#最初的范围：在下标0~n-1中找x    while i <= j:#范围合法，i在j的左边 k = (i + j) // 2#找中点k，整除，保证下标为整数 if x == A[k]:#与中点比较     return k#找到并返回 elif x < A[k]:     j = k - 1 else:     i = k + 1    return -1  # 没找到返回-1A = [2, 4, 6, 14, 19, 20, 34, 88]index = binary_search(A, 21)print(index)

编程关键：

  • 目标区域，用下标、索引来表示
  • 左、右边界：分别用i,j来表示

查找数字和

给定1万个数字，从中找出两个数，使得两个数的和恰好等于一个指定的数X，输出这2个数的值（可能找不到）。

  • 算法1：对前面n-1个数循环（外循环），每次循环，都将这个数和它后面的数进行配对（内循环），时间复杂度是O(n2)。
  • 算法2：先排序，然后对前n-1个元素循环，每次循环时，对元素a，到后面用二分法搜索X-a，虽然排序的复杂度是O(nlogn)，但是循环的复杂度也是O(nlogn)，因此优于算法1。

算法1:使用循环

import timeimport randomt = time.time()random.seed(17)  # 随机数种子，使得A里面的数固定# 在1到百万的范围内，生成1万个数字A = [random.randint(1, 1000000) for i in range(10000)]X = 37711  # 要搜索的数字和founded = Falsefor i in range(len(A) - 1):  # 遍历前n-1个数    for j in range(i + 1, len(A)): if A[i] + A[j] == X:     print(A[i], A[j])     founded = True     break  # 会跳到下一个break    else: continue  # 没有break就到这里执行    break  # 确保退出外循环if not founded: print('没找到')print(time.time() - t)
3071 34640时间：2.8977272510528564

算法2：使用二分法

import randomdef binary_search(A, x):    i, j = 0, len(A) - 1    while i <= j: k = (i + j) // 2 if x == A[k]:     return k elif x < A[k]:     j = k - 1 else:     i = k + 1    return -1  # 没找到返回-1random.seed(17)  # 随机数种子，使得A里面的数固定# 在1到百万的范围内，生成1万个数字A = [random.randint(1, 1000000) for i in range(10000)]A.sort()  # nlognX = 37711  # 要搜索的数字和founded = Falsefor i, a in enumerate(A[:-1]):  # 遍历前n-1个数    idx = binary_search(A[i + 1:], X - a)  # logn    if idx != -1: print(a, A[i + 1 + idx]) founded = True breakif not founded: print('没找到')
3071 34640

求方程的根

求一元一次方程、一元二次方程的根：
ax+b=0,ax2+bx+c=0用公式求解。
一元n（n>=3）次方程呢？ x3-5x2+10x-80 = 0
非多项式方程呢？ xex-1=0

f(x) = x3-5x2+10x-80 = 0，若求出的根是a，则要求 |f(a)| <= 10-5。
对f(x)求导，得f’(x)=3x2-10x+10。由一元二次方程求根公式知方程 f’(x)= 0 无解，因此f’(x)恒大于0。故f(x)是单调递增的。
这种单调性说明方程只有一个根。

算法1：使用循环

# 1.画图，看到2道拐import matplotlib.pyplot as pltimport numpy as npx = np.linspace(-20, 20)y = x ** 3 - 5 * x ** 2 + 10 * x - 80# 设置横轴纵轴刻度范围plt.axis([-20, 20, -500, 500])plt.grid('on')  # 绘制网格plt.plot(x, y)plt.show()'''找到：1.解在5附近2.f(2.5)0'''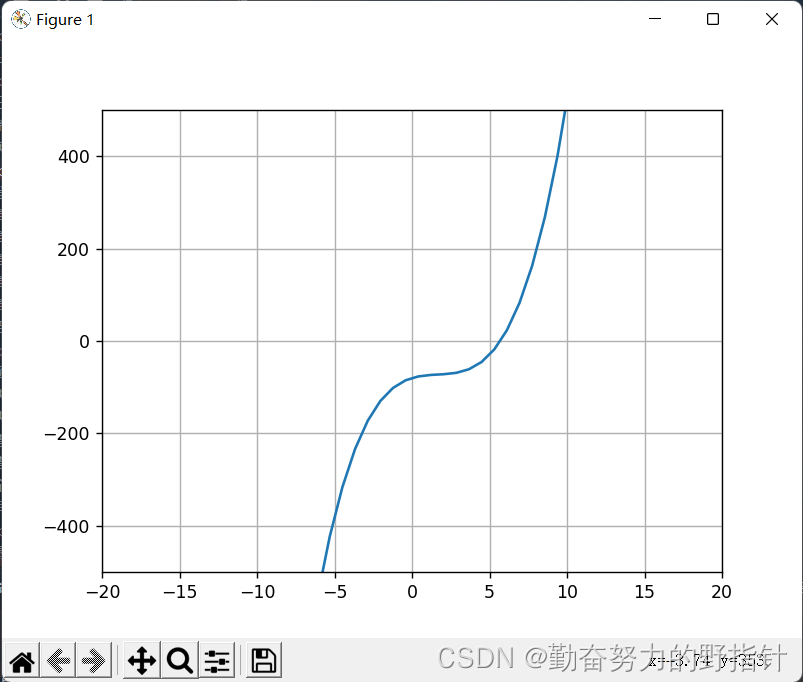

python算法思维笔记(1)
刻度范围可以不断尝试，务必让曲线穿过横轴，以此来观察根的大致范围

观察图像，易知 f(0) 0,所以区间[0,10]内必然有且只有一个根。
如何找出这个根？
思路1：从0开始尝试，每次给x一个小的增量，计算y的值，|y|应当逐步减小，当|y|开始增加时，上一个值就是解。相当于在[x1,x2]区间内，以某个间隔delta产生(x2-x1)/delta个值，然后找出其中使得f(x)满足条件的值。

存在的问题：
A 这个增量必须足够小，否则可能会不满足条件： |f(a)| <= 10-5
B 需要循环的次数可能超出你的想象。

E = 1e-5x = 5.7  delta = 1E-6  # x的增量while True:    x += delta    y = x ** 3 - 5 * x ** 2 + 10 * x - 80    print('x=', x, 'y=', y)    if abs(y) <= E: break

算法的问题：

  1. delta选得过小时，可能会进入死循环，因为不满足退出循环的条件。
  2. x的初值距离结果越远，需要的时间越长，每多间隔1个单位，需要多循环1/delta次。

问题规模
显然，[x1,x2]区间内，存在(x2-x1)/delta个值要尝试（当然尝试可能因为找到结果而在中途停止），因此，问题规模就是n=(x2-x1)/delta； delta的取值与E和方程的形式相关。

时间复杂度:O(n)。

算法2：使用二分法
f(x) = x3-5x2+10x-80

  1. 根在区间[0,10]当中，尝试计算f(5)；5=(0+10)/2
  2. f(5) =-56<0, 根在区间[5,10]当中，尝试计算f(7.5)；7.5=(5+10)/2
  3. f(7.5)=135.625>0, 根在区间[5,7.5]当中，尝试计算f(6.25)；6.25=(5+7.5)/2
  4. f(6.25)= 31.328125>0,根在区间[5,6.25]当中，尝试计算f(5.625)；5.625=(5+6.25)/2
  5. f(5.625)= -3.974609375<0,根在区间[5.625,6.25]当中，尝试计算f(5.9375)；5.9375=(5.625+6.25)/2
  6. f(5.9375)= 12.42…>0,根在区间[5.625, 5.9375]当中，尝试计算f(5.78125)； 5.78125=(5.625+5.9375)/2
  7. f(5.78125)= 3.92 …>0,根在区间[5.625, 5.78125]当中，尝试计算f(5.703125)；5.703125=(5.625+5.78125)/2
E = 1e-5x1, x2 = 0, 10y = 1  # 随意的较大的初值while abs(y) > E:    x = (x1 + x2) / 2    y = x ** 3 - 5 * x ** 2 + 10 * x - 80    if y >= 0: x2 = x    else: x1 = xprint('x=', x, 'y=', y)
x= 5.70508599281311 y= 3.1834457274726446e-06

对于区间[x1,x2]，每次循环后，区间变为[x1,(x1+x2)/2]或[(x1+x2)/2,x2]，区间都会缩小为原来的一半。因此，区间[x1,x2]中需要尝试的值的数目为n=(x2-x1)/delta，二分法求根的时间复杂度为O(logn)

对于非单调函数，怎么处理？
可以绘图考察曲线的形状，观察不同的根所在的单调区间，然后分别指定区间来求不同的根
例如： f(x) = x4-5x2+10x-80 = 0,2个根分别在下面单调区间中：[-5, -2.5]，[2.5, 5.0]

求和问题

给定4组数（元素总数n相同，n<=100 ），在每组数中找一个数，使得4个数之和为0，求共有多少组数符合条件（不同的索引号算不同的结果）。
例如：
[-45, -41, -36, -36, 26, -32]
[22, -27, 53, 30, -38, -54]
[42, 56, -37, -75, -10, -6]
[-16, 30, 77, -46, 62, 45]
结果为：5

这5组数为：
(-45, -27, 42, 30), (26, 30, -10, -46), (-32, 22, 56, -46),(-32, 30, -75, 77), (-32, -54, 56, 30).

算法1：使用循环
最容易想到的思路是暴力求解，即设计4重循环，对每种可能的组合进行求和，每当和为0时，计数器加1即可。
暴力法的时间复杂度为O(n4)，n为100时，循环108次，估算时间为102秒（循环106算1秒）。

import randomimport timet = time.time()random.seed(7)  # 固定随机数种子，每次产生相同序列A, B, C, D = [], [], [], []n = 100for i in range(n):    A.append(random.randint(-10000, 10000))    B.append(random.randint(-10000, 10000))    C.append(random.randint(-10000, 10000))    D.append(random.randint(-10000, 10000))result = 0for i in range(n):    for j in range(n): for k in range(n):     for l in range(n):  if A[i] + B[j] + C[k] + D[l] == 0: result += 1print('result=', result)print(time.time() - t)
result= 3302所用时间：13.324002027511597

算法2：使用二分法
解题思路：考虑若4个数a+b+c+d=0,则a+b=-(c+d)。如果找出所有的a+b，放入一个列表X，对于任一个-(c+d)，若能在X中找到，则存在1个解，而搜索的过程可以利用二分法提高效率。

1 对列表A和B进行所有可能的求和，将结果放入列表X，对X排序。
2 对列表C和D进行所有可能的求和，求和结果取负数，记为key，然后用二分法在X中搜索key，如果找到，则存在一组数据的和为0。

时间复杂度，对n2个元素排序：O(n2log(n2))=O(n2log(n))

# 有问题的代码# X中可能存在一些相同的数，因此可能会漏掉一些结果。def binary_search(A, x):    i, j = 0, len(A) - 1    while i <= j: k = (i + j) // 2 if x == A[k]:     return k elif x < A[k]:     j = k - 1 else:     i = k + 1    return -1  # 没找到返回-1import randomrandom.seed(7)  # 固定随机数种子，每次产生相同序列A, B, C, D = [], [], [], []n = 100for i in range(n):    A.append(random.randint(-10000, 10000))    B.append(random.randint(-10000, 10000))    C.append(random.randint(-10000, 10000))    D.append(random.randint(-10000, 10000))X = []result = 0for i in range(n):    for j in range(n): X.append(A[i] + B[j])X.sort()for i in range(n):    for j in range(n): key = -(C[i] + D[j]) idx = binary_search(X, key) if idx != -1: result += 1print('result=', result)
result= 2738

解决方案
改进二分搜索函数，使其返回2个索引号，分别指示找到的第一个和最后一个元素的索引号，记为p1,p2，则每次二分搜索之后，result+=(p2-p1+1)。

例如，在下面的序列中搜索12：
3,6,9,12,12,12,18,20
返回：3,5
则解的总数增加(5-3+1)=3

def binary_search1(A, x):    i, j = 0, len(A) - 1    while i <= j: k = (i + j) // 2 if x == A[k]:     p1 = p2 = k     while p1 > 0 and A[p1 - 1] == x: p1 -= 1     while p2 < len(A) - 1 and A[p2 + 1] == x: p2 += 1     return p1, p2 elif x < A[k]:     j = k - 1 else:     i = k + 1    return -1, -1  # 保持返回值形状一致import randomrandom.seed(7)  # 固定随机数种子，每次产生相同序列A, B, C, D = [], [], [], []n = 100for i in range(n):    A.append(random.randint(-10000, 10000))    B.append(random.randint(-10000, 10000))    C.append(random.randint(-10000, 10000))    D.append(random.randint(-10000, 10000))X = []result = 0for i in range(n):    for j in range(n): X.append(A[i] + B[j])X.sort()for i in range(n):    for j in range(n): key = -(C[i] + D[j]) p1, p2 = binary_search1(X, key) if p1 != -1: result += (p2 - p1 + 1)print('result=', result)
result= 3302

棍子的膨胀

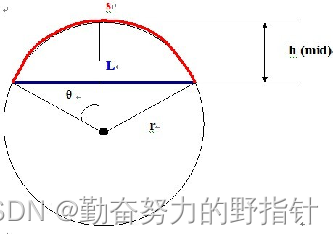
一根长为L的细棍被加热后，温度增加了n摄氏度，那么其新的长度为S=(1+n*C)*L。中间的C是热膨胀系数。当一根细棍被夹在两面墙中间然后被加热，它会膨胀，其形状会变成一个弧，而原来的细棍(加热前的细棍)就是这个弧所对的弦。

解题思路
如图，蓝色为杆弯曲前，长度为L；红色为杆弯曲后，长度为S；h是所求。
依题意知S=(1+n*C)*L
又从图中得到三条关系式;
1 角度→弧度公式 θr = S/2
2 三角函数公式 sinθ= L/2r
3 勾股定理 r2 – ( r – h)2 = (L/2)2

四条关系式简化后，可得：
r=4ℎ2+L2/8ℎ … (1)
S=2r∗arcsin(L/2r)…(2)
要求（1）式的h，唯有先求r
但是由于（2）式是三角函数式，直接求r比较困难
python算法思维笔记(1)
采用二分法求方程的根的思路，在h的值的范围内枚举h的值，由式(1)计算出对应的r，再由式(2)计算出S’，然后计算S’与给出的S之间的差异。若差异小于一个很小的值（例如10-5），则这个h就是要求的结果。

h下界为0，上界为L/2，因为当L穿过圆心时，L=2r，h=L/2，此时，S=πr= π L/2，而题目中说明了S<=3/2L。

使用二分法，在[0,L/2]之间枚举h进行尝试，若差异小于10-5，则问题解决。

网络标签：

相关问题