Java的入门学习-关于环境变量与程序运行原理
我在刚刚学习JAVA时只是抱着高中时期的:”跟着老师走,我就能理解一切“的心态,按部就班按着老师所讲的去学习,并非没用,但也不能算很有用,学校的老师讲课会顾及难度,不会向我们去教导一些更深层次的东西,当我去问老师时,老师给的回答往往是让我去网络里寻求答案,对啊,现在是互联网的时代,AI遍布我们的生活各处,技术文档由众多大佬分享,于是我对于一些当时不是很理解的地方做了我自认为的“浅层深挖”,目的是为了帮助我更加去理解原理,而不是只是迷迷糊糊的做一个打代码工具。
一.为什么我们要去配置环境变量?
在我刚刚接触JAVA的时候,老师课上交给我们的第一个任务,便是\"配置环境变量\",这对于还是萌新的我而言十分的困难,反复的配置失败以及一次次尝试让我不由得想:“为什么我们要配置JAVA的环境变量呢?”
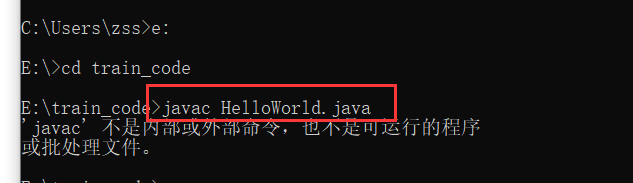
如图中,我在没有配置环境变量之前尝试在我的E:\\train_code下去执行命令:
javac HelloWord.java ,结果弹出提示:“javac不是内部或外部命令,也不是可执行程序”。
为什么呢?为什么会出现“javac不是内部或外部命令”这个错误呢?我明明已经安装了JAVA!
原来在未配置环境变量时,系统无法在任意路径下找到javac.exe,因为系统默认只在当前目录和PATH环境变量指定的路径中搜索可执行文件。在环境变量没被配置时,系统根本不知道javac.exe到底在哪里。
javac.exe通常藏在 C:\\Program Files\\Java\\你的jdk版本名称\\bin 里面
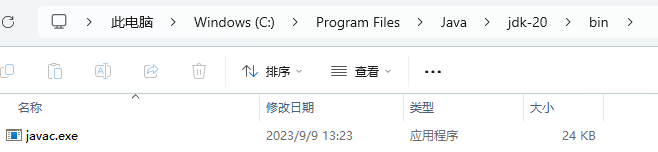
而我如果需要运行我的.java程序,我需要JDK(Java Development Kit - JAVA开发工具包)中bin目录下的javac.exe来对.java程序进行“编译”,那么我想你应该有一些理解了,之所以要配置环境变量,是为了使得我们的这个.java程序无论位于我们电脑的哪个盘符(C: / D: / E:........)下的哪个文件下,都可以通过javac.exe来进行对.java程序的“编译”。
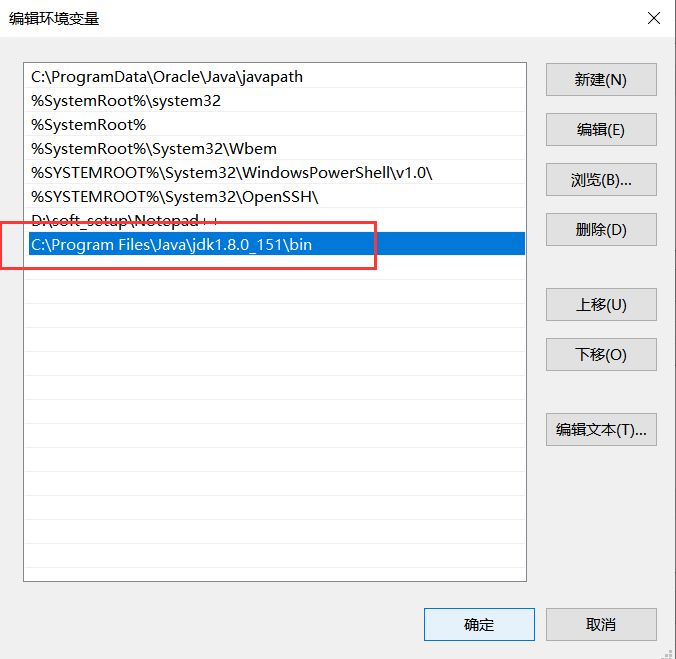
环境变量PATH的配置,配置PATH后,无论当前目录在哪里,系统都会在C:\\Program Files\\Java\\jdk-xx\\bin中搜索javac.exe,可以理解为就是将我所配置的这个路径当作一个环境,我执行哪个文件都相当于是我在这个环境下去执行的,当然也就能使用这个环境内的工具了,所以我们并不是不配置环境变量就无法运行JAVA项目,配置环境变量后,我们就可以在任意目录下编译和运行Java程序,无需每次切换到JDK的bin目录。
二.“编译”是什么过程?JAVA程序又是怎么样去执行的呢?
在“一”里面我们提到了一个词,叫做“编译”,这个词本身我们是没少听的,我们常说编译器,编译器,难道编译的作用就是把程序在我们的计算机运行吗?事实上,编译只是我们程序运行这个大过程中的一个小过程,举个例子,比如运行C语言程序,我们并不是只依靠编译去运行这个程序,而是先通过编译将开发者写出的这些由英文字母组成的代码,转换为机器所能看懂的二进制的机器码,然后再由机器去执行这个二进制的机器码,但是JAVA呢?JAVA也是这样吗?
实则不然,JAVA程序的运行过程要更多一点,因为Java拥有一个优势:那就是JAVA可以实现跨平台,通常称之为“一次编写,到处运行”(Write Once, Run Anywhere, WORA)。
1.为什么JAVA可以实现跨平台而C/C++不行呢?
C/C++都是直接由对应操作系统的编译器来编译为.exe的可执行文件,之后直接运行的,他们所生成的这个.exe里面都是针对特定平台的机器码,所以C/C++并不能够实现跨平台运行,Windows的.exe就是Windows的,Linux的就是Linux的。
2.JAVA的运行过程较为特殊,JAVA的运行过程为:
首先,开发者写出一份.JAVA程序,拿给环境变量里的JDK说:“我这里有个JAVA程序,请你帮我运行他。”,然后JDK中的javac.exe就会把你给他的JAVA程序编译为一份.CLASS的字节码文件(.class文件就是JAVA实现跨平台的关键),并且对你说:“这个你得等我会儿,我这里呢得先处理下你的程序,然后交给统一部门对你这个程序做更细化的处理。”
然后,这个.CLASS文件会被交给JVM,JVM类似每个手机厂商分布在各个城市的手机专卖店,虽然门店服务的地区不同,但是门店都是这个手机厂商旗下的,也就是说虽然不同操作系统下的JVM是不同的,但他们都有一个相同的“接口”来使得他们能以不同的JVM实现来达成同一个功能:那个功能就是他们都能够将这个.CLASS文件进行动态解释或者编译执行
关于JAVA与C/C++的运行过程(更清晰的展示):
-
C/C++:源码 → 编译为平台特定的机器码 → 直接运行。
-
Java:源码 → 编译为平台无关的字节码 → JVM解释/编译执行。
字节码文件的核心作用:
跨平台(平台无关性):一次编译,JVM运行(Windows/Linux/Mac通用)。
安全可控:JVM检查代码,防止崩溃或病毒。
统一生态:Java/Kotlin等语言最终都变成字节码,互相兼容。
高效执行:JIT编译热点代码,速度接近C++。
一句话总结:字节码是Java跨平台的“通用语言”,由JVM翻译执行,兼顾安全性和性能。
三.JAVA最基础的程序代码
public class Main { public static void main(String[] args) { System.out.println(\"Hello, World!\"); }} 我所打的第一个JAVA程序,便是这个“Hellow,World!”,我一开始就对这个神奇的东西很不理解,这个String[] args是个什么玩意?main前面这一大串又是啥啊?
关于main
main方法是一个特殊的方法,它定义了JAVA程序的起始位置。如果没有这个方法,JVM就无法启动程序。如图,可以看到,如果一个程序中没有main方法,那么这个程序甚至无法运行。
注意,这里说无法运行并发完全无法运行:
-
Java 9+支持模块化启动,可通过
jlink定制启动类。 -
但初学者场景下,main仍是标准入口。
关于String[] args
main方法不只是一个简单的入口,他里面传入的参数,也就是:String[] args参数(事实上,String[] args作为一个参数,参数名并不强行要求为args,你甚至可以把它改成aaas),但要注意:
-
虽然args可以改名,但约定俗成用
args,提高代码可读性。 -
其他常见命名如
argv(来自C传统)。
程序可以通过这个参数来处理用户输入的动态数据,String[] args中存储了当该程序在终端或者命令提示符中运行JAVA程序时,人为通过命令添加的额外参数,比如我在终端中执行:
java 类名 参数1 参数2 ... 那么这个时候,arg[0] = \"参数一\",而arg[1] = \"参数二\",让我们来验证一下吧:
public class MyProgram { public static void main(String[] args) { // 获取参数数组的长度 int numArgs = args.length; System.out.println(\"命令行参数数量: \" + numArgs); // 遍历并打印每个参数 for (int i = 0; i < numArgs; i++) { System.out.println(\"args[\" + i + \"] = \" + args[i]); } }} 我们在终端执行 java MyProgram \"hellow world\" 123 ,我们运行程序会输出:
命令行参数数量: 2args[0] = hello worldargs[1] = 123 关于System.out.println()
当我写出代码时,我看着我打印出来的Hellow,World!陷入了一个思考,为什么这个名为System.out.println的东西能够将它后面括号内的内容打印出来呢?
![]()
这里面,System是JDK提供的工具类,out是其静态字段(类型为PrintStream),println是PrintStream的方法。这些代码是Java标准库的一部分,初期只需知道它是输出语句,后期可深入研究IO流和标准输出的设计.
当我们的鼠标按住“Ctrl”键的同时将鼠标指针移到这三个单词的任意一个上面时,他会被高亮,这个时候我们点进去,你就会发现:
它跳转到了一个我们不知道的地方,这里就是JDK的源代码,我们的这个语句就是在这里被定义的,所以本质上我们只是将大佬们定义好的方法拿过来去使用。
个人想说的话:
我是一名学习JAVA等编程语言的普通学生,如果我的这篇文章帮助到了你,我很开心,同时如果我的文章有问题,请各位发现后对我所说的有问题的部分做出修改和指正(请详细一些),避免他人看到造成误导。


