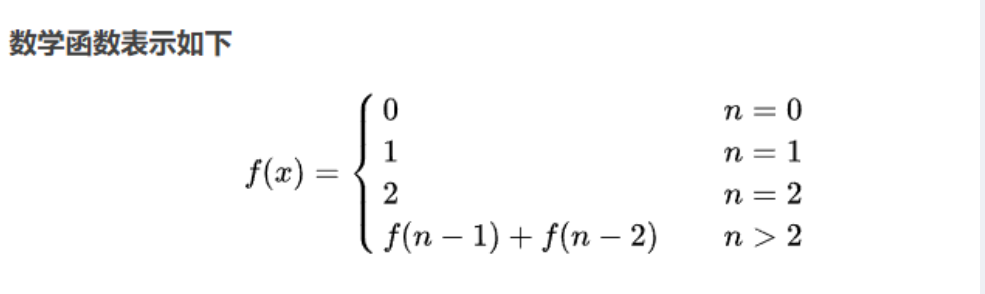目录

• 🍅题目描述
• 🍅画图分析
• 🍅思路分析
• 🍅代码实现

🍅题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

🍅画图分析

和上篇文章讲到的汉诺塔问题一样，我们还是由简到繁，从最简单的情况开始考虑：

只有一级台阶的情况：

只有一级台阶的时候，显然只有一种跳法。

有两级台阶的情况

有两级台阶的时候，青蛙有两种跳法。

跳一阶，在跳一阶：

直接跳两阶：

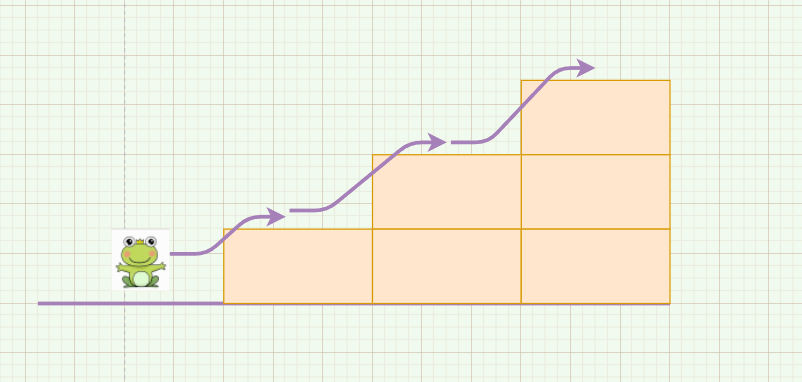
有三级台阶的情况：

有三级台阶的时候，青蛙有三种跳法。

跳一阶，再跳一阶，再跳一阶：

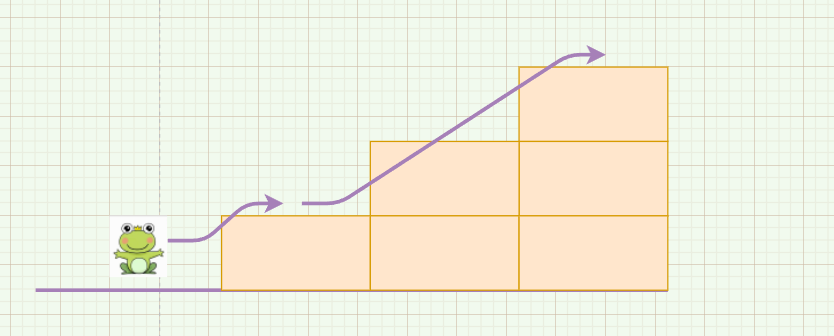
跳一阶，再跳两阶：

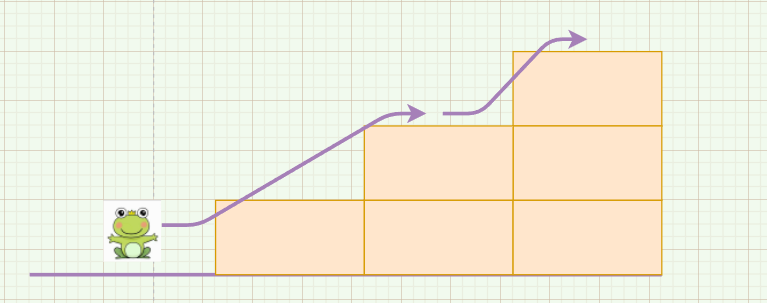
跳两阶，再跳一阶：

🍅思路分析

经过上面的分析，我们知道了一级、二级和三级台阶的跳法，现在要我们求 n 级台阶的跳法，我们可以这样思考：

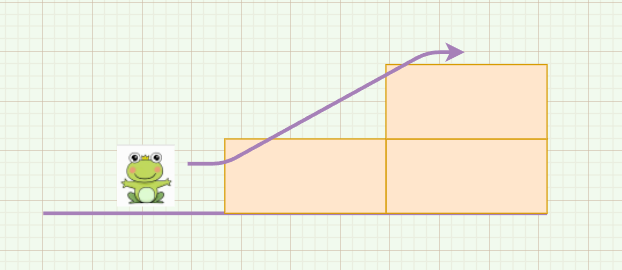
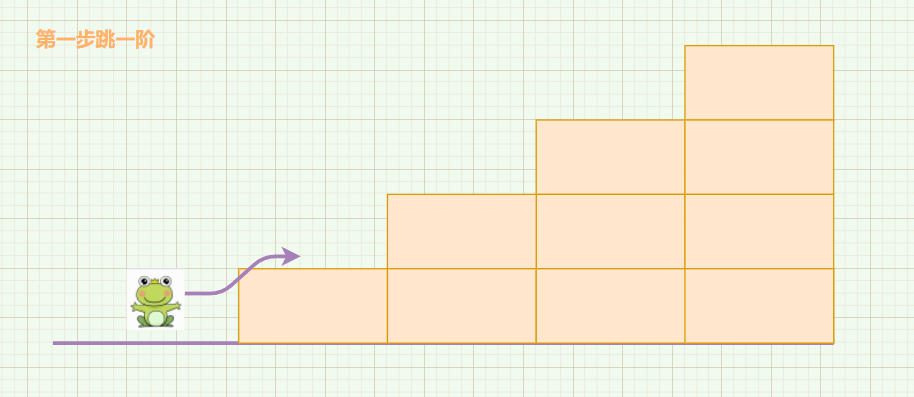
假设这里有 n 级台阶，那么我们第一步就有两种选择：

跳一阶：

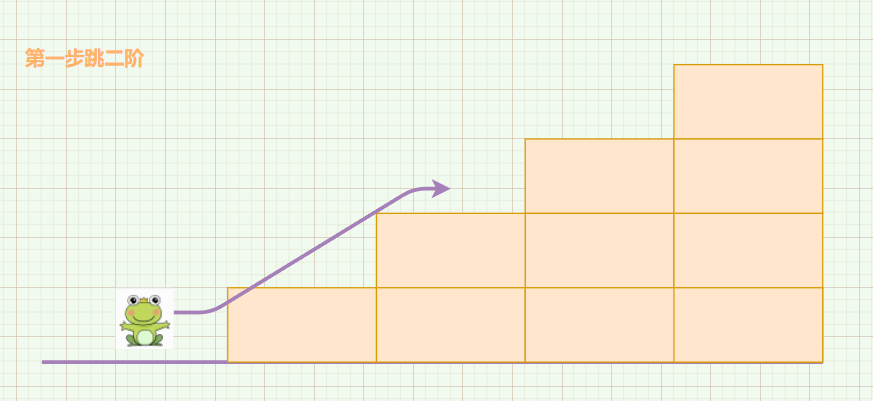
跳两阶：

假设 n 级台阶的跳法一共有 f(n) 种，那么：

当我们第一步选择跳一阶时，就剩下 n-1 级台阶，即剩下的跳法是 f(n-1) 种。

当我们第一步选择跳二阶时，就剩下 n-2 级台阶，即剩下的跳法是 f(n-2) 种。

所以 n 级台阶的跳法总数应该是二种跳法之和（第一步可能跳一阶，也可能跳二阶）：f(n-1) + f(n-2) 。

我们可以发现青蛙跳台阶的规律和斐波那契数列非常相似，仅仅是开始的值不一样而已。

🍅代码实现

递归写法

#includeint Frog(int n){if (n < 3){return n;   //当n小于3时，直接返回n即可}else{return Frog(n - 1) + Frog(n - 2);  //当n大于等于3时，执行递归}}int main(){int n = 0;printf("请输入台阶数->");scanf("%d", &n);int num = Frog(n);printf("跳法总数为：%d\n", num);return 0;}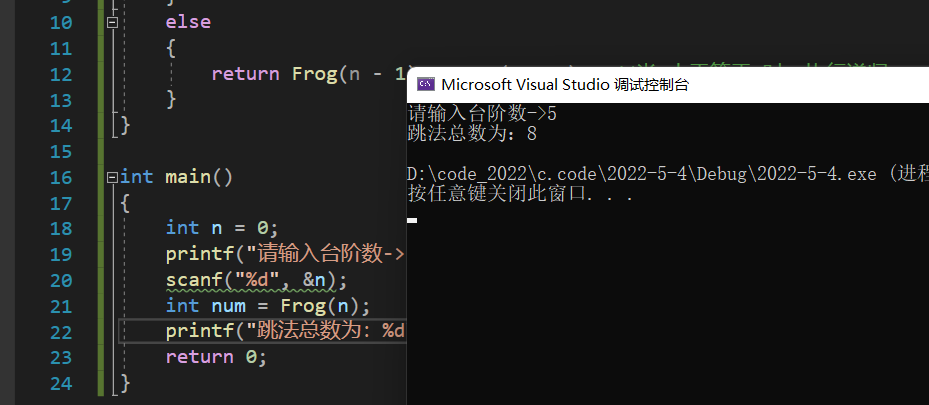

非递归写法：

#includeint Frog(int n){if (n < 3){return n;    //当n小于3时，直接返回n即可}else{int f1 = 1;int f2 = 2;int sum = 0;while (n > 2){sum = f1 + f2;f1 = f2;f2 = sum;n--;}return sum;}}int main(){int n = 0;printf("请输入台阶数->");scanf("%d", &n);int num = Frog(n);printf("跳法总数为：%d\n", num);return 0;}