未来属于那些相信梦想，并愿意为之付诸行动的人。

前言

整数二分法

指定的数字(binary_search)

第一个大于等于X的位置(lower_bound/upper_bound)

不大于X的最后一个位置

数的范围

整数二分模板

浮点数二分法

 浮点数二分法模板

总结:

前言

今天我跟大家一起学习二分查找,想必提到这大家会说，这么简单有什么好说的,其实当我们做题的时候会发现，会出现很多边界问题,往往让人头疼，通过这篇文章搞清楚这些边界,就算还是没搞懂，会提供模板帮助大家刷题。学完这一章，不仅可以掌握二分查找,还可以轻松解决下面问题:

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode） (leetcode-cn.com)
167. 两数之和 II - 输入有序数组 - 力扣（LeetCode） (leetcode-cn.com)

300. 最长递增子序列 - 力扣（LeetCode） (leetcode-cn.com)

整数二分法

首先我们从猜数游戏开始说起,在这个游戏中，玩家A从一个范围中选择一个数(数字范围是[1,1000],假如玩家A选择了400;)，然后玩家B开始猜这个数，如果玩家B猜的这个数X，比400小，他就会从[X+1,1000]重新猜,如果玩家B猜这个数X，比400大,那么400一定在[1,X-1]中,只需要在这里猜就行了,很明显每次选择当前范围的中间数去猜，就能尽可能快的猜出来数字.

那么从这个游戏中我们引申出来一个经典的问题:如何在一个严格递增的序列A中找出给定的数A囊？这还不简单：直接线性扫描序列中所有元素,如果当前元素恰好为X,则表明查找成功;如果找到最后都没有发现要找的那个数字X，则表明查找失败.这种查找方法很直接，不过他的时间复杂度为O(n),数字小一点没关系，当我们的序列是10^5时,这个就是一个很庞大的工程，很显然接受不了?

那我们能不能受猜数游戏的启发去优化这个查找过程囊?这里我们引出二分查找.二分查找是基于有序序列的查找算法，该算法一开始令[left,right]为整个序列的下标区间,然后每次测试当前[left，right]的中间位置mid=(left+right]/2,.判断A[mid]与查找元素X的大小关系。

1.如果A[mid]等于X则说明查找成功退出即可          A[mid]==X

2.如果A[mid]>X,则说明X肯定不在右边,令right=mid-1缩小查找范围   [left,mid-1]

3.如果A[mid]<X,则说明X肯定不在左边,令left=mid+1缩小查找范围    [mid+1,right]

这样就高效很多了，每次查找都可以去除当前区域的一半元素,因此时间复杂度为O(logn);

 为了更好的理解这个查询过程，接下来我们来模拟这个二分查找过程.

指定的数字(binary_search)

现在我们需要从序列A={1,5,6,8,9,11,15,16,20}中查找数字11的位置,其中序列是0下标是0到8(下标1到9也是没问题的大家下去可以模拟一下)

1.[left,right]=[0,8],因此下标中点是mid=(left+right)/2=4;A[mid]=A[4]=9;9<11;说明需要在    [mid+1,right]范围内继续找,因此left=mid+1=5;

2.[left,right]=[5,8],因此下标中点是mid=(left+right)/2=6;A[mid]=A[6]=15;15>11;说明需要在[left,mid-1]范围内继续查找,因此right=mid-1=5;

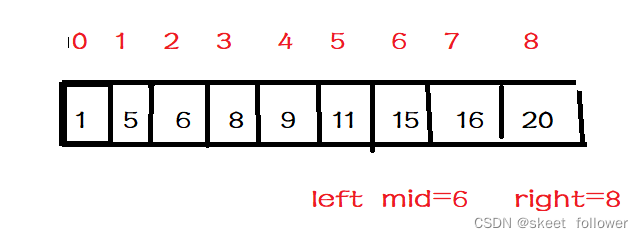
3.[left,right]=[5,5],因此下标中点mid=(left+right)/2=5;A[mid]=A[5]=11;11=11;说明找到了需要查找的数X，返回下标5

ok,有了上面的基础下面我们来写代码吧。

int binarySearch(int A[],int left,int right,int x){   int mid;//mid为left和right的中点  while(leftx)  right=mid-1;//往左子区间[left,mid-1]查找    elseleft=mid+1;  //往右子区间[mid+1,right]查找  }  return -1;//查找失败返回-1}

如果序列是递减的,只需要把A[mid]>x改为A[mid]<x

二分法也可以用递归形式进行

//二分区间为左闭右闭的[left,right],传入的初值为[0,n-1]int binarySearch(int* a, int left, int right, int key){while (left > 1);int number = a[mid];if (number  key){return binarySearch(a, left, mid - 1, key);}elsereturn mid;}}

这里了解了,我们接下来要更进一步的讨论:如果递增序列A中的元素可能重复，那么如何对给定的欲查询元素x,求出序列中第一个大于等于x的元素的位置L以及不大于X的最后一个位置?

第一个大于等于X的位置(lower_bound/upper_bound)

例如对下标0开始，有5个元素的序列为{1,3,3,3,6}来说,如果要查询3，则应当得到L=1，R=4;如果要查询5，则应当得到L=R=4;如果要查询6.应该得到L=4,R=5;而查询如果是8，则应该得到L=R=5.显然如果序列中没有X，那么L和R也可以理解为假设序列中存在X，则X应当在的位置.

做法其实和前面的很类似,下面我们来分析一下,假设当前的二分区间为左闭右闭区间[left,right]，那么可以根据mid位置处的元素与欲查询元素x的大小来判断应当往哪个区间查找:

1.如果A[mid]>=x,说明第一个大于等于x的位置一定在mid处或者在mid的左侧，应该往左子区间[left,mid]继续查找,即令right=mid;

2.如果A[mid]<x,说明第一个大于等于x的元素的位置一定在mid的右侧，应往右区间[mid+1,right]继续查找,即令left=mid+1;

代码:

//A[]为递增，x为查询数字;//二分上下界为左闭右闭的[left,right],传入的初值为[0,n]int low_bound(int A[],int left,int right,int x){ int mid;  while(left=x)  right=mid;//中间的数大于等于x，往左边区间找[left,mid]   else    left=mid+1;//中间的数小于x，往右边区间找[mid+1,right] }  return left;}

注意:1.循环条件为什么是left<right不是left<=right？这是由问题本身决定的.在上面题目中，需要当元素不存在返回-1,这样当left>right是[left,right]就不再是闭区间，可以作为元素不存在的判定原则，因此left<=right满足时循环应当一直执行。但是如果要是区间返回第一个大于等于x的元素，就不需要判断元素本身是不是存在,因为他就算不存在返回的也是"假设他存在，他应该的位置",于是当left==right时， 刚好能夹出唯一的位置，就是需要的结果.

2.由于left==right时while停止,因此最后返回left,right都可以.

3.二分的初始区间应该能覆盖到所有可能返回的结果.下界为0肯定的，那上界为什么是n，不是n-1,考虑到欲查询元素有可能比序列中任何数字都要大，此时应该返回n（即假设它存在，它应该在的位置).故初始化区间为[0,n];当然也有的题目要求不在则返回-1,这时候就不需要取到n,具体问题具体分析.

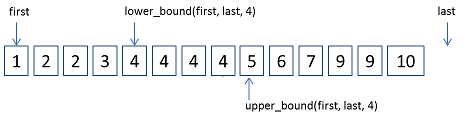
拓展: 其实这就是C++中lower_bound()函数的用法,返回第一个大于等于x数的位置,不存在则返回最后一个数的下一个位置;对应的也有个upper_bound()函数的用法，它是返回第一个大于x数的位置;这个大家可以去实现下，其实就是A[mid]>=x换成A[mid]>x就可以了.这两个函数大家可以去了解下,具体实现上面其实已经介绍了.

不大于X的最后一个位置

这个实现就比上面的稍微难一点了.所以我这里需要引入个例题:

数的范围

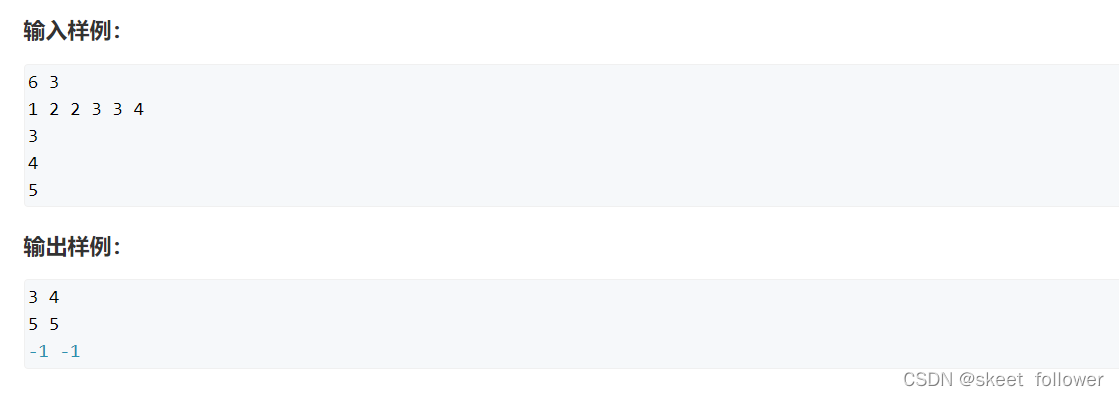简述下题意就是:就是查询一个数的起始位置和终止位置，不存在这个数就返回-1，所以这里取值范围不需要向上面一样取到n(这里不需要输出最后一个数的下一个位置)；

需要写两个二分，一个需要找到>=x的第一个数，另一个需要找到<=x的最后一个数。查找不小于x的第一个位置，较为简单(上面已经讲过了):直接放代码

int l = 0, r = n - 1;while (l > 1;    if (a[mid] < x)  l = mid + 1;    else    r = mid;}

查找不大于x的最后一个位置，便不容易了：

int l1 = l, r1 = n;while (l1 + 1 > 1;    if (a[mid] <= x)  l1 = mid;    else    r1 = mid;}

这里我看到了一位小哥写的解释，超级清楚，拿过来给大家看一下:AcWing 789. 数的范围（详细分析二分过程） - AcWing（大家也可以去这看)

为什么不令r = mid - 1呢？因为如果按照上一个二分的写法，循环判断条件还是l < r,当只有两个元素比如2 2时，l指向第一个元素，r指向第二个元素，mid指向第一个元素，a[mid] <= x，l = mid还是指向第一个元素，指针不移动了，陷入死循环了，此刻l + 1 == r，未能退出循环。
那么直接把循环判断条件改成l + 1 < r呢？此时一旦只有两个元素，l和r差1，循环便不再执行，查找错误。
所以这里出现了二分的典型错误，l == r作为循环终止条件，会出现死循环，l + 1 == r作为循环终止条件，会出现查找错误 

问题如何解决，一种方法就是将查找的区间设置为左闭右开，比如待查找元素在[0,n - 1]范围内，可以写成[0,n)，令r = n，这时候只有两个元素时，r是取最右边元素的后一个位置的，l和r相差2，还会执行循环。
现在再来理解上一段的r1 = mid，说明a[mid] > x时，r = mid就表示待查找元素会是在r的左边，因为r是开区间。上面这种写法修改了循环条件使得二分不会死循环，修改了区间的开闭性使得不会查找错误。另一种解决办法就是：

int l = 0, r = n - 1;while (l > 1; if (a[mid] <= x) l = mid; else r = mid - 1; }

到这里核心的代码已经展示完毕，大家可以下去自己去做做.

整数二分模板

bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：int bsearch_1(int l, int r){    while (l > 1; if (check(mid)) r = mid;    // check()判断mid是否满足性质 else l = mid + 1;    }    return l;}// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：int bsearch_2(int l, int r){    while (l > 1; if (check(mid)) l = mid; else r = mid - 1;    }    return l;}

浮点数二分法

首先介绍如何计算根号2的近似值。

对于f(x)=x^2来说,在x属于[1,2]范围内,f(x)是随着x的增大而增大的，这就给使用二分法创造了条件,即可以用如下策略来逼近根号二的值。(这里不妨以精确到10^-5为例)

令浮点数left和right的初值分别是1和2，然后根据left和right的中点mid处f(x)的值与2的大小来选择子区间进行逼近.

如果f(mid)>2,说明mid>根号2,应当在[left，mid]的范围内继续逼近,故令right=mid;

 如果f(mid)<2,说明mid<根号2,应该在[mid,right]的范围内继续逼近,故令left=mid.

 上面两个步骤当right-left<10^-5时结束.

代码:

const double eps=1e-5;double f(double x){   return x*x;}double calsqrt(){    double left=1,right=2,mid;  while(right-left>eps)  {    mid=(left+right)/2;   if(f(mid)>2)  right=mid;   else  left=mid;  }  return mid; }

 浮点数二分法模板

bool check(double x) {/* ... */} // 检查x是否满足某种性质double bsearch_3(double l, double r){    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求    while (r - l > eps)    { double mid = (l + r) / 2; if (check(mid)) r = mid; else l = mid;    }    return l;}

总结:

以上就是二分查找的所有知识点了,下面就是多练题了,二分法还是用的很多的像装水问题,木棒切割,快速幂，求方程根等问题。

墨言文学成语大全