【信号与系统】连续时间信号与系统的频域分析

1、典型周期矩形脉冲傅里叶级数实现

A=1;T=2;tao=1;t=-2:0.001:2;N=input('Number of harmonic=')X0=A*tao/T;w0=2*pi/T;X=X0*ones(1,length(t));for k=1:1:N;X=X+2*X0*sinc(k*w0*tao/2/pi)*cos(k*w0*t);end plot(t,X)

n=5时

n=20时

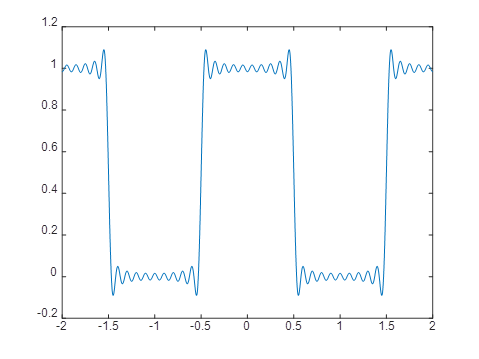
2、典型非周期信号指数信号x=exp(-2*t)的傅里叶变换

syms x tx=exp(-2*t)subplot(311);ezplot(x);title('指数信号')X=fourier(X)X=simplify(X) //化简 subplot(312) ezplot(abs(X))title('幅度谱')subplot(313)ezplot(angle(X)) //复数相角，提取相位title('相位谱')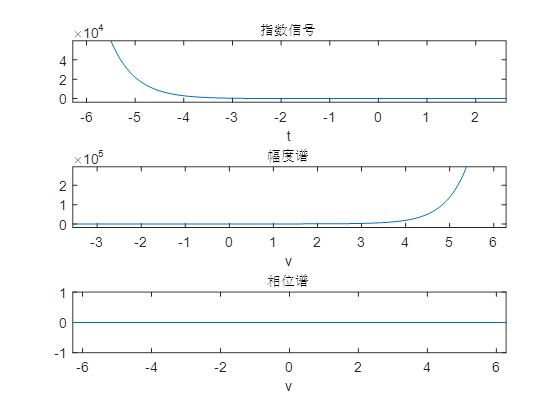 

3、验证傅里叶变换的对称性

N=3001;t=linspace(-15,15,N);f=pi*[heaviside(t+1)-heaviside(t-1)];dt=30/(N-1); M=500;w=linspace(-5*pi,5*pi,M);F=f*exp(-j*t'*w)*dt;subplot(2,2,1),plot(t,f);axis([-2,2,-1,4]);xlabel('t');ylabel('f(t)');subplot(2,2,2), plot(w,real(F));axis([-20,20,-3,7]);xlabel('w');ylabel('F(w)=F[f(t)]');f1=sinc(t/pi);F1=f1*exp(-j*t'*w)*dt;subplot(2,2,3),plot(t,f1);xlabel('t');ylabel('f1(t)-F(t)/2*pi'); subplot(2,2,4),plot(w,real(F1));axis([-2,2,-1,4]);xlabel('w');ylabel('F1(w)=F[f1(t)]=f(w)');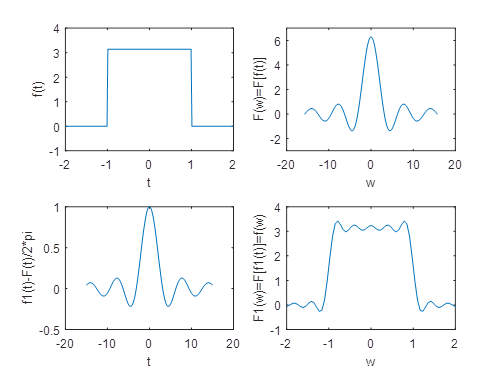

4、 x = 2exp(2t)的FFT快速算法

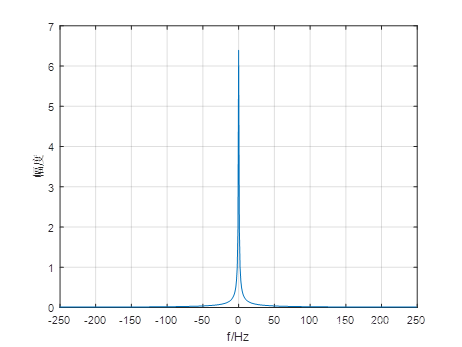
fs=500;%采样率f1=5;%信号频率f2=10;%信号频率T=1;%时宽1sn=round(T*fs);%采样点个数t=linspace(0,T,n);%时域横坐标x = 2*exp(2*t);figure(1);plot(t,x);%画时域图xlabel('t/s')grid onX = fftshift(fft(x./(n))); %用fft得出离散傅里叶变换f=linspace(-fs/2,fs/2-1,n);%频域横坐标，注意奈奎斯特采样定理，最大原信号最大频率不超过采样频率的一半figure(2)plot(f,abs(X));%画双侧频谱幅度图xlabel('f/Hz')ylabel('幅度')grid on

原信号x = 2exp(2t)

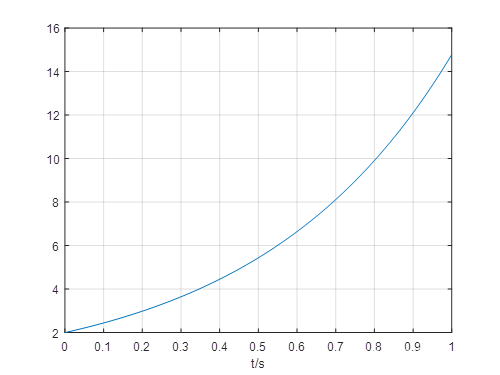
fft离散傅里叶变换

5.根据微分方程实现系统函数的幅度响应和相位响应

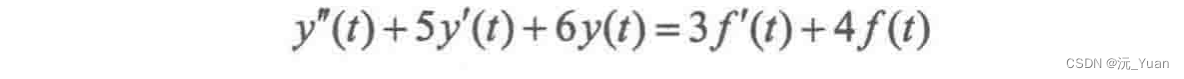
w=0:0.01:5b=[1];a=[1 2 2 1];h=freqs(b,a,w);subplot(2,1,1);plot(w,abs(h));subplot(2,1,2);plot(w,angle(h));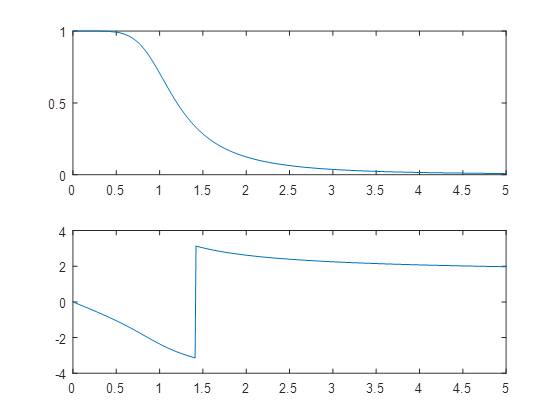

3，傅里叶变换的性质有如下：