目录

1.链表的公共节点

 2.分割链表

3.判断链表是否成环

4.链表入环的第一个节点

1.链表的公共节点

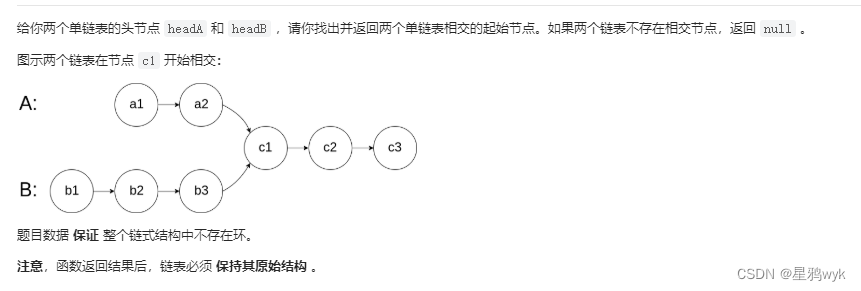
这题用到的依旧是双指针

思路1：

首先遍历两个链表分别求出它们的长度，二者的差值就是较长的链表指针先走的步数，然后两个指针同时往后移动，当二者相等的时候的节点就是链表的公共节点

代码如下：

public class Solution {    public ListNode getIntersectionNode(ListNode headA, ListNode headB) { if(headA==null||headB==null) {     return null; } int lenA=0; int lenB=0; ListNode curA=headA; ListNode curB=headB; while(curA!=null) {     lenA++;     curA=curA.next; } while(curB!=null) {     lenB++;     curB=curB.next; } int i=Math.abs(lenA-lenB); curA=headA; curB=headB; if(lenA>lenB) {  while(i>0) {      curA=curA.next;      --i;  }     } else {  while(i>0) {      curB=curB.next;      --i;  }     } while(curA!=curB && curA!=null && curB!=null) { curA=curA.next;     curB=curB.next; } if(curA==null||curB==null) {     return null; } return curB;     }}

思路2：

这题的关键是两个链表的长度不一样，所以两个指针如果要在第一个公共节点相遇 的话就需要使两个指针在节点的长度是一样的，我们不妨让A链表加上链表B的长度，链表B加上链表A的长度，这样就确保了两个指针同时出发可以在公共节点前相遇

具体实现就是A链表的指针走完A的路程之后，将其放到链表B的头节点，B中的指针同理

代码如下：

public class Solution {    public ListNode getIntersectionNode(ListNode headA, ListNode headB) { if(headA==null || headB==null) {     return null; } ListNode pa=headA; ListNode pb=headB; while(pa!=pb) {     if(pa==null) {  pa=headB;     } else {  pa=pa.next;     }     if(pb==null) {  pb=headA;     } else {  pb=pb.next;     } }//如果两个链表不相交，最后pa和pb都会是null return pa;     }}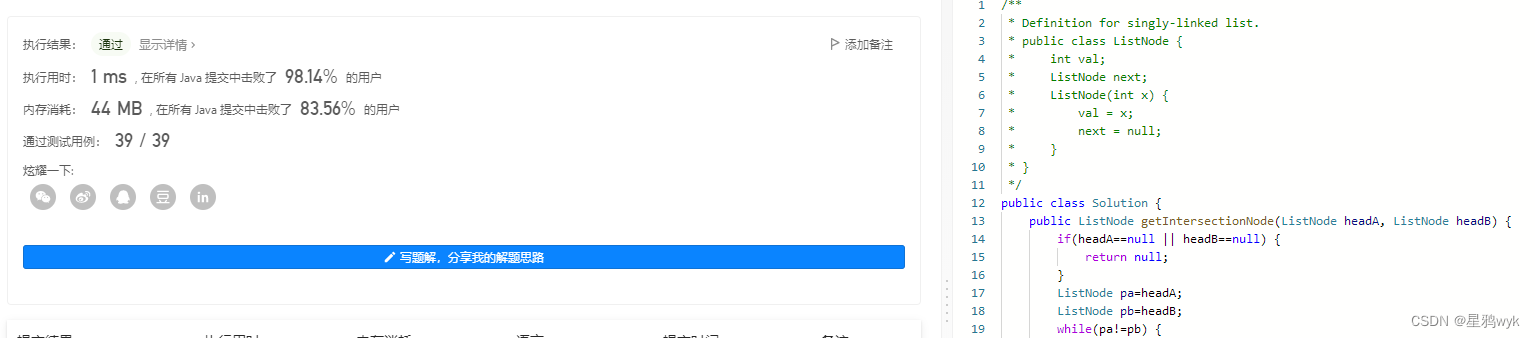

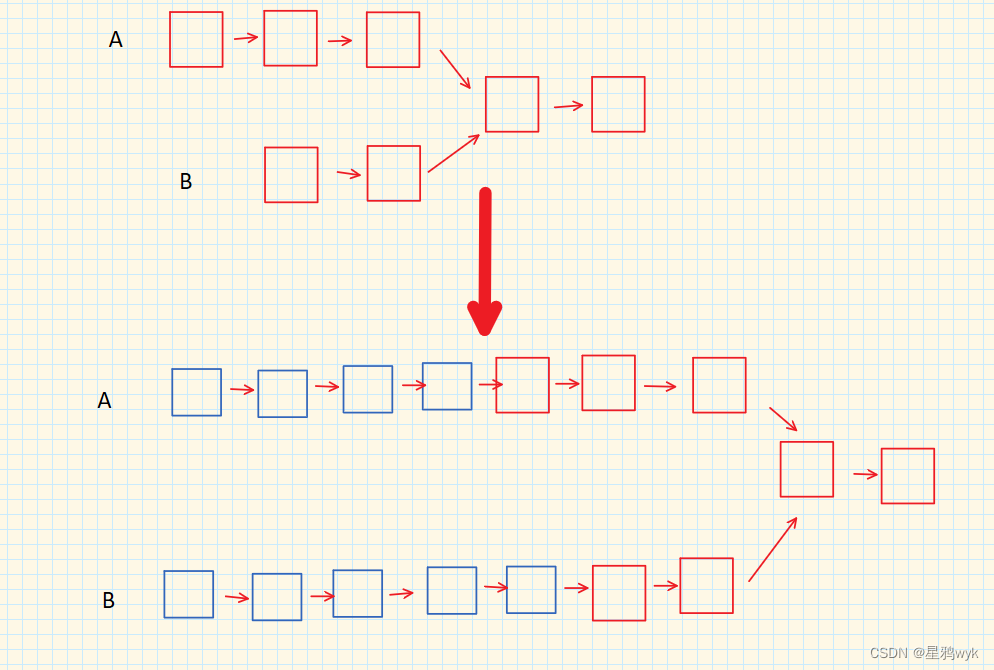
 2.分割链表

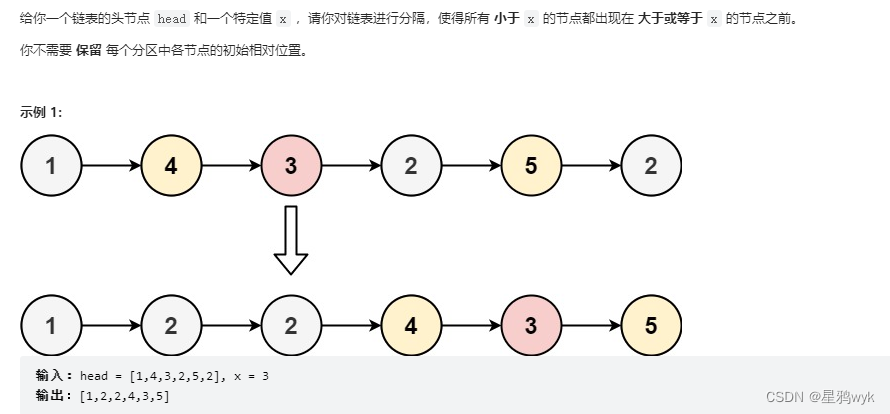
 思路：

我们先把链表换成数组来想想该怎么写

新建两个数组，一个存放小于x的值，另一个存放大于等于x的值，遍历原数组将值存进去，然后将两个新建的数组进行合并，链表也是同样的思路，注意链表为空的情况

代码如下：

class Solution {    public ListNode partition(ListNode head, int x) { ListNode head1=new ListNode(1); //题目没有提供不带参数的构造方法，返回其指向的地址即可 ListNode h1=head1; ListNode head2=new ListNode(2); ListNode h2=head2; ListNode cur=head; while(cur!=null) {     if(cur.val<x) {  h1.next=cur;  h1=h1.next;     } else {  h2.next=cur;  h2=h2.next;     }     cur=cur.next; }if(head1.next==null) { //原链表的值都不小于x的情况    return head2.next; } h1.next=head2.next; h2.next=null;//最后一个节点的地址要置空 return head1.next;    }}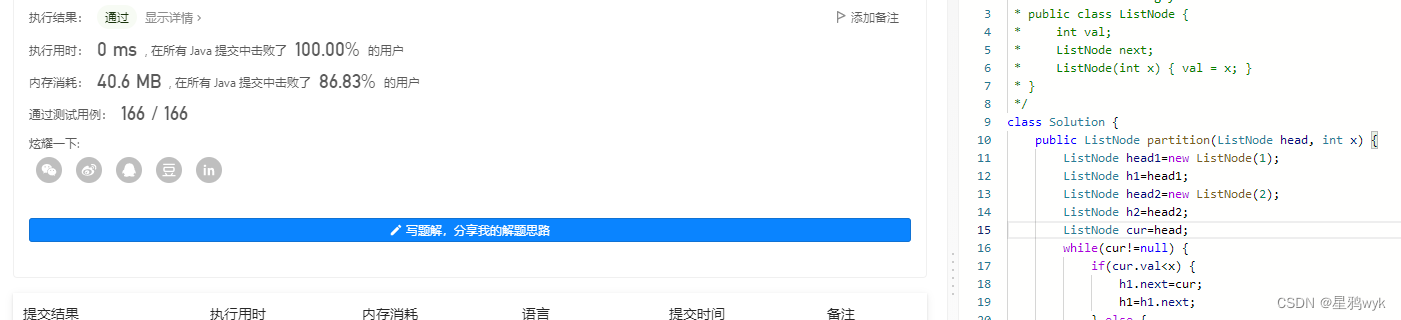

3.判断链表是否成环

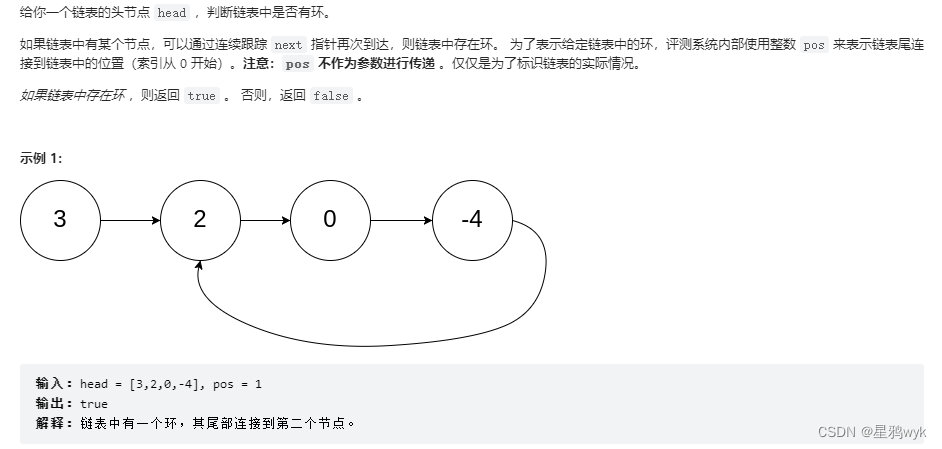
 思路：

依旧是快慢指针

fast一次走两步，slow一次走一步，如果链表有环，那么两个指针就会都进入环内，因为fast比slow快，所以fast和slow会在环内的某个位置相遇

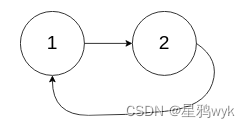
注：fast走两步是最稳妥的方法，实例中有给出如下的环

假设让fast走3步，slow走1步，二者是不会相遇的

代码如下：

public class Solution {    public boolean hasCycle(ListNode head) { if(head==null||head.next==null) {     return false; } ListNode fast=head; ListNode slow=head; while(fast!=null && fast.next!=null) {     slow=slow.next;     fast=fast.next.next;     if(fast==slow) {  return true;     } } return false;    }}

4.链表入环的第一个节点

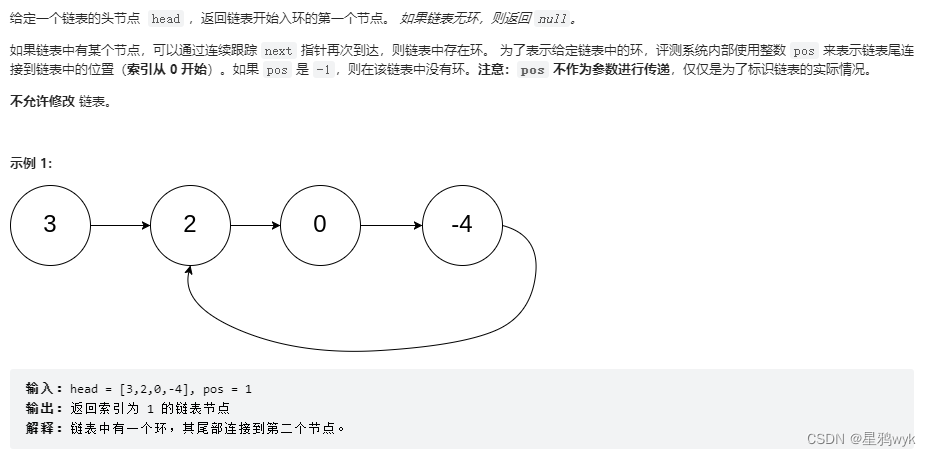
 思路：

依旧是快慢指针

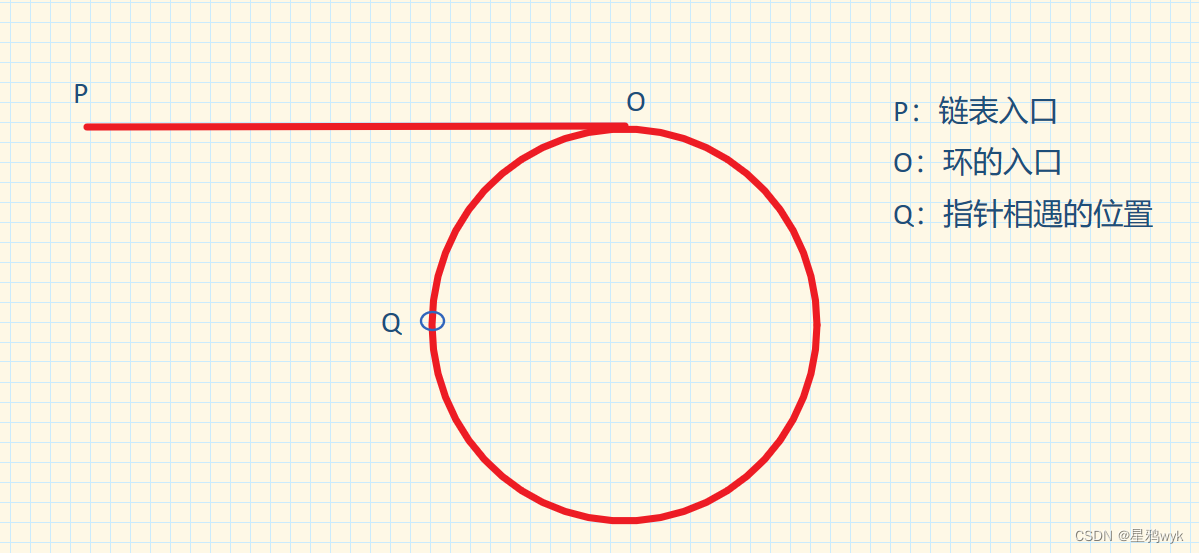
先说一个结论：

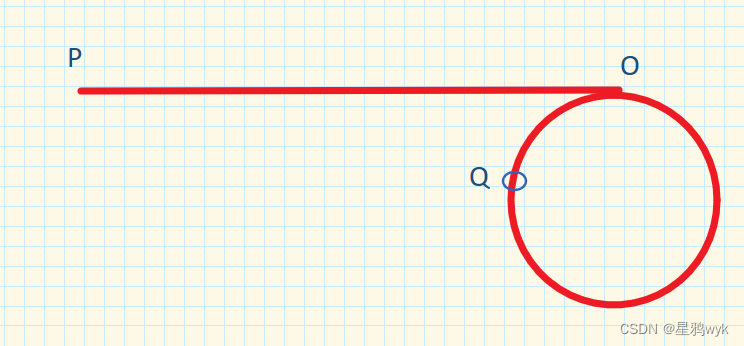
链表如果成环，那么OQ和OP的长度是相等的（后面会进行推导）

依据这个结论，我们先让fast和slow在环中相遇，然后再将slow放在链表头节点处，之后二者都是每次走一步，最后相遇的地方就是入环的第一个节点

代码如下：

public class Solution {    public ListNode detectCycle(ListNode head) { if(head==null||head.next==null) {     return null; } ListNode fast=head; ListNode slow=head; while(fast!=null && fast.next!=null) {     slow=slow.next;     fast=fast.next.next;     if(fast==slow) {  slow=head;  while(fast!=slow) {      slow=slow.next;      fast=fast.next;  }  return slow;     } } return null;    }}

推导：

为方便讲解，还是先做一些标记

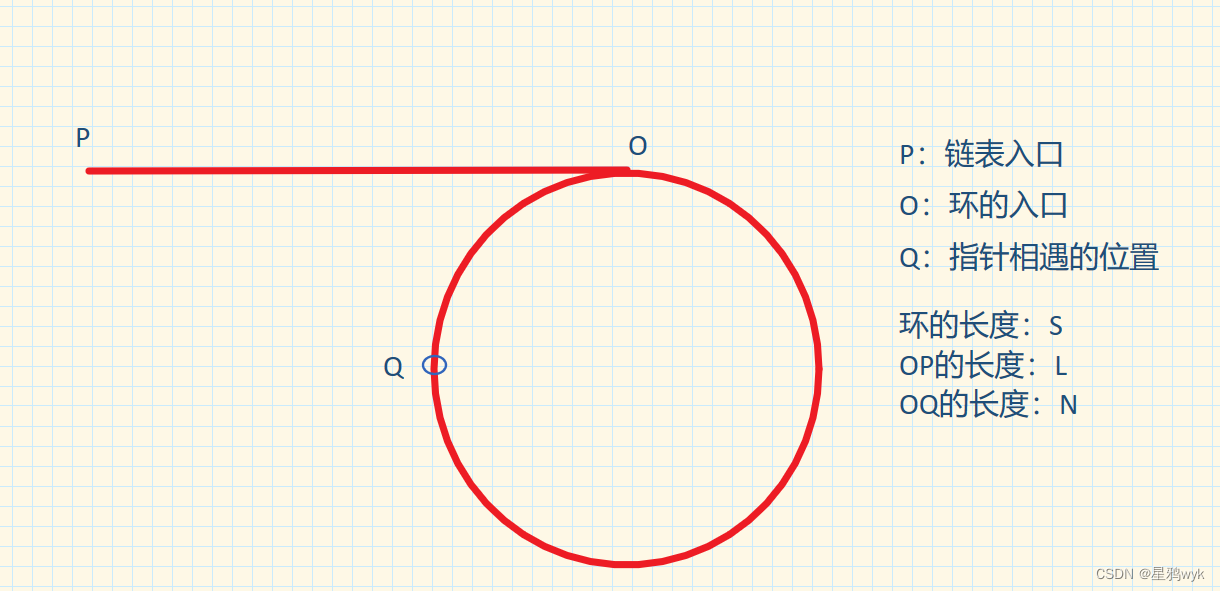
S=L的情况就不必讨论了

• S>L

 当slow到达O点的时候，此时fast走过了环的大半路程但还没有走完一圈，它们相遇的大致位置如下

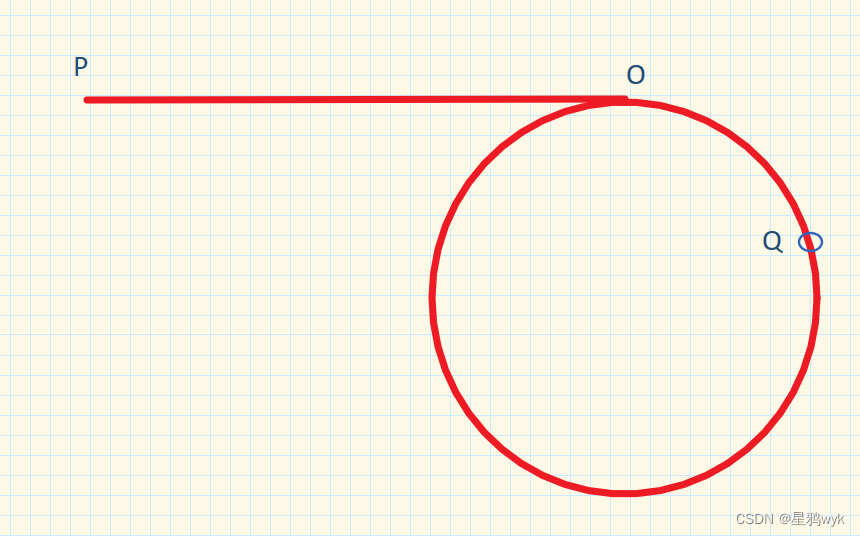
此时slow所走的路程为L+N，fast为L+N+S，又因为fast的速度是slow的两倍

所以有L+N+S=2*(L+N)

化简之后就是L=S-N

S-N是环内从Q到O的距离，这个距离和L相等

• S<L

当slow到达O点的时候，fast可能在环内走过了不止一圈，我们假设fast走过了x圈，相遇的大致位置如图

 slow的路程为L+S-N，fast为L+x*S+S-N

fast路程同样是slow的两倍：L+x*S+S-N=2*(L+S-N)

化简之后结果为L=(x-1)*S+N

前面的(x-1)*S可以省略，因为此时fast是在转圈，结果为L=N

链表的题目就到这，完