💛 前情提要💛

本章节是数据结构的栈和队列的相关知识~

接下来我们即将进入一个全新的空间，对代码有一个全新的视角~

以下的内容一定会让你对数据结构有一个颠覆性的认识哦！！！

❗以下内容以C语言的方式实现，对于数据结构来说最重要的是思想哦❗

以下内容干货满满，跟上步伐吧~

---

作者介绍：

🎓 作者： 热爱编程不起眼的小人物🐐
🔎作者的Gitee：代码仓库
📌系列文章&专栏推荐： 《刷题特辑》、 《C语言学习专栏》、《数据结构_初阶》

📒我和大家一样都是初次踏入这个美妙的“元”宇宙🌏 希望在输出知识的同时，也能与大家共同进步、无限进步🌟

---

📌导航小助手📌

• 💡本章重点
• 🍞一.栈的概念
• • 🥐Ⅰ.什么是栈
  • 🥯Ⅱ.总结
• 🍞二.栈
• • 🥐Ⅰ.结构
  • 🥐Ⅱ.LIFO原则
  • 🥐Ⅲ.实现
• 🍞三.栈插口实现
• • 🥐Ⅰ.初始化栈
  • 🥐Ⅱ.入栈操作
  • 🥐Ⅲ.出栈操作
  • 🥐Ⅳ.取栈顶数据
  • 🥐Ⅴ.判断栈是否为NULL
  • 🥐Ⅵ.获取栈内数据的个数
  • 🥐Ⅶ.栈的销毁
  • 🥯Ⅷ.总结
• 🍞四.队列的概念
• • 🥐Ⅰ.什么是队列
  • 🥯Ⅱ.总结
• 🍞Ⅴ.队列
• • 🥐Ⅰ.结构
  • 🥐Ⅱ.FIFO原则
• 🍞Ⅵ.队列插口实现
• • 🥐Ⅰ.初始化队列
  • 🥐Ⅱ.入队列操作
  • 🥐Ⅲ.出队列操作
  • 🥐Ⅳ.取队头数据
  • 🥐Ⅴ.取队尾数据
  • 🥐Ⅵ.判断队列是否为NULL
  • 🥐Ⅶ.获取队列结点个数
  • 🥐Ⅷ.队列的销毁
  • 🥯Ⅸ.总结
• 🫓总结

---

💡本章重点

• 栈的概念

• 栈的结构&实现

• 队列的概念

• 队列的结构&实现

---

🍞一.栈的概念

🥐Ⅰ.什么是栈

• 栈是一种特殊的线性表

• 只允许在固定的一端进行插入和删除元素操作

❗综上：

• 栈中的数据遵守后进先出LIFO（Last In First Out）的原则

• 即元素的先进后出的原则

🥯Ⅱ.总结

✨综上：就是栈的概念啦~

➡️简单来说：栈是一种特殊的的线性表，在插入和删除数据时都要在固定的一端进行操作，且遵循先进后出的原则

---

🍞二.栈

🥐Ⅰ.结构

• 逻辑结构
  

🥐Ⅱ.LIFO原则

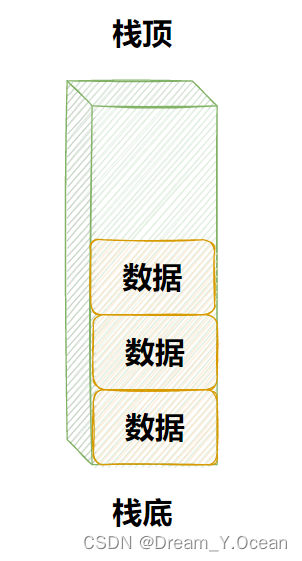
💡在栈中：

• 进行数据插入和删除操作的一端称为栈顶

• 另一端称为栈底

👉栈的操作：

• 栈的插入数据的操作叫：进栈/压栈/入栈

• 栈的删除数据的操作叫：出栈【此过程中遵循LIFO原则】

⭐通过上图，我们可知：

• 在栈中插入数据是在栈顶进行入数据的

• 在栈中删除数据也是在栈顶进行出数据的

✨有了以上对栈的概念后，我们便可以实现它啦~

🥐Ⅲ.实现

💡简单来说： 实现栈的本质就是实现栈的入栈和出栈操作【期间遵循LIFO原则】

➡️我们可以通过三种我们学过的数据结构去实现它：

• 1️⃣ 单链表：可以通过单链表去头插、头删去模拟实现栈数据的入、出

• 2️⃣带头+双向+循环链表：这个结构去实现栈的操作非常便捷，可以快速的找到栈顶和栈尾，并对栈顶实现插入和删除数据的操作

• 3️⃣顺序表：也可以实现上述的操作

👉由上述我们可知：

• 带头循环双向链表虽然便捷，但它比其它结构插入和删除时的操作要多出几条语句，所以本次不适用

• 链表与顺序表相比之下，相对而言顺序表的结构实现更优一些，虽然需要增容，但顺序表的效率一定程度上可以弥补且数组在尾上插入数据的代价比较小

✨综上：

• 我们便用顺序表去实现栈

❗所以下面我们开始实现栈的接口

---

🍞三.栈插口实现

对于数据结构的接口实现，一般围绕增、删、查、改的内容

💡如下的实现围绕此原码进行：

typedef int STDataType;typedef struct Stack{STDataType* a;int capacity; //表示容量int top; // 表示栈顶}Stack;Stack st;StackInit(&st);

🥐Ⅰ.初始化栈

1️⃣初始化栈的函数声明：

void StackInit(Stack* pst);

2️⃣初始化栈函数的实现：

void StackInit(Stack* pst){assert(pst);pst->a = (STDataType*)malloc(sizeof(STDataType) * 4);pst->top = 0;pst->capacity = 4;}

🥐Ⅱ.入栈操作

👉简单来说： 对栈顶进行插入数据

➡️实现： 即在顺序表中为尾插

❗特别注意：

• 当顺序表为NULL（空表）的时候，尾插即是在头插

• 当顺序表满了的时候，需要增容

✊动图示例：

1️⃣入栈的函数声明：

void StackPush(Stack* pst, STDataType x);

2️⃣入栈函数的实现：

void StackPush(Stack* pst, STDataType x){assert(pst);//检查是否需要增容if (pst->top == pst->capacity){STDataType* tmp = (STDataType*)realloc(pst->a,sizeof(STDataType) * pst->capacity * 2);if (tmp == NULL){printf("realloc fail\n");exit(-1);}pst->a = tmp;pst->capacity = pst->capacity * 2;}pst->a[pst->top] = x;pst->top++;}

🥐Ⅲ.出栈操作

👉简单来说： 对栈顶出一个元素

➡️实现： 即在顺序表中为尾删

❗特别注意：

• 顺序表的尾删并不是真正意义上的删除，而是通过top来控制下标从而访问不到以达到删除的效果

• 需要判断是否为NULL（空表），空表就不能做出栈操作了

✊动图示例：

1️⃣出栈的函数声明：

void StackPop(Stack* pst);

2️⃣出栈函数的实现：

void StackPop(Stack* pst){assert(pst);assert(!StackEmpty(pst)); //判断是不是 非空的pst->top--;}

🥐Ⅳ.取栈顶数据

👉简单来说： 返回栈顶的数据

➡️实现： 即返回一个顺序表中下标为top-1的数据

❗特别注意：

• 需要判断顺序表此时是否为NULL（空表），如果是则不能返回了

1️⃣返回栈顶数据的函数声明：

STDataType StackTop(Stack* pst);

2️⃣返回栈顶数据函数的实现：

STDataType StackTop(Stack* pst){assert(pst);//需要判断顺序表是不是 不为空assert(!StackEmpty(pst));return pst->a[pst->top - 1];}

🥐Ⅴ.判断栈是否为NULL

👉简单来说： 就是判断top是否为0

➡️实现： 因为top表示的是栈内的数据个数【top-1才是当前栈顶数据的下标】

• top为0，栈就为空

• 否则，栈为非空

1️⃣判断栈是否为NULL的函数声明：

bool StackEmpty(Stack* pst);

2️⃣判断栈是否为NULL函数的实现：

bool StackEmpty(Stack* pst){assert(pst);return pst->top == 0; }

🥐Ⅵ.获取栈内数据的个数

👉简单来说： 返回栈内数据个数

➡️实现： 返回top即可

1️⃣返回栈内数据个数的函数声明：

int StackSize(Stack* pst);

2️⃣返回栈内数据个数函数的实现：

int StackSize(Stack* pst){assert(pst);return pst->top; //top就是大小}

🥐Ⅶ.栈的销毁

👉简单来说： 对栈进行空间释放

➡️实现： 与顺序表的销毁操作一样

1️⃣栈的销毁的函数声明：

void StackDestory(Stack* pst);

2️⃣栈的销毁函数的实现：

void StackDestory(Stack* pst){assert(pst);free(pst->a);pst->a = NULL;pst->capacity = pst->top = 0;}

🥯Ⅷ.总结

✨综上：就是栈的接口实现的内容啦~

➡️相信大家对栈有不一样的看法了吧🧡

---

🍞四.队列的概念

🥐Ⅰ.什么是队列

• 队列是一种特殊的线性表

• 只允许在一端进行插入数据操作

• 在另一端进行删除数据操作

❗综上：

• 队列中的数据遵守后进先出FIFO（First In First Out）的原则

• 即元素的先进先出的原则

🥯Ⅱ.总结

✨综上：就是队列的概念啦~

➡️简单来说：队列是一种特殊的的线性表，在插入和删除数据时都要在不同的两端进行操作，且遵循先进先出的原则【整体与栈的规则刚好相反】

---

🍞Ⅴ.队列

🥐Ⅰ.结构

• 逻辑结构
  

🥐Ⅱ.FIFO原则

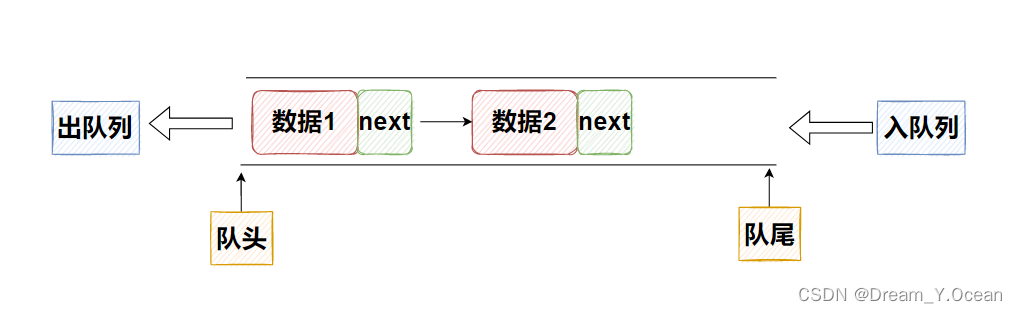
💡在队列中：

• 进行数据插入的一端称为队头

• 进行数据删除的一端称为队尾

👉队列的操作： 我们采用单链表的结构实现【因为如果使用顺序表的结构，出队列在数组头上出数据，需要整体往前移动，效率会比较低】

• 队列插入数据的操作

• 队列的删除数据的操作【此过程中遵循FIFO原则】

✨有了以上对队列的概念后，我们便可以实现它啦~

---

🍞Ⅵ.队列插口实现

对于数据结构的接口实现，一般围绕增、删、查、改的内容

💡如下的实现围绕此原码进行：

typedef struct Queue{QueueNode* head; //定义一个头指针QueueNode* tail; //定义一个尾指针}Queue;

typedef int QDataType;//定义一个结点typedef struct QueueNode{struct QueueNode* next;QDataType data;}QueueNode;

❗特别注意：

• 因为队列不像单链表需要遍历每个结点去访问每个结点的数据，所以我们只需要获取队头和队尾的数据即可

• 这也是为什么设置两个指针：头指针、尾指针

🥐Ⅰ.初始化队列

1️⃣初始化队列的函数声明：

void QueueInit(Queue* pq);

2️⃣初始化队列函数的实现：

void QueueInit(Queue* pq){assert(pq);pq->head = pq->tail = NULL;}

🥐Ⅱ.入队列操作

👉简单来说： 对队列的队尾进行插入数据

➡️实现： 即控制尾指针让新的结点尾插进来

❗特别注意：

• 当链表为NULL（空表）的时候，尾插即是在头插

✊动图示例：

1️⃣入栈的函数声明：

void QueuePush(Queue* pq,QDataType x);

2️⃣入栈函数的实现：

void QueuePush(Queue* pq, QDataType x){assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){printf("malloc fail\n");exit(-1);}newnode->data = x;newnode->next = NULL;//入队列过程：if (pq->tail == NULL){assert(pq->head == NULL);pq->head = pq->tail = newnode;}else{pq->tail->next = newnode; //链上去pq->tail = newnode; //再成为新的尾巴}}

🥐Ⅲ.出队列操作

👉简单来说： 对队列的队头删除一个元素

➡️实现： 即在链表中为头删

❗特别注意：

• 需要判断是否为NULL（空表），空表就不能做出队列操作了

✊动图示例：

1️⃣出队列的函数声明：

void QueuePop(Queue* pd);

2️⃣出队列函数的实现：

void QueuePop(Queue* pq){assert(pq);//判断是不是 非空assert(!QueueEmpty(pq)); if (pq->head->next == NULL){//只有一个结点的时候free(pq->head);pq->head = pq->tail = NULL;} else{QueueNode* next = pq->head->next;free(pq->head);pq->head = next;}}

🥐Ⅳ.取队头数据

👉简单来说： 返回队头的数据

➡️实现： 即返回链表中头指针指向的结点的数据

❗特别注意：

• 需要判断链表此时是否为NULL（空表），如果是则不能返回了

1️⃣返回队头数据的函数声明：

QDataType QueueFront(Queue* pq);

2️⃣返回队头数据函数的实现：

QDataType QueueFront(Queue* pq){assert(pq);assert(!QueueEmpty(pq));return pq->head->data;}

🥐Ⅴ.取队尾数据

👉简单来说： 返回队尾的数据

➡️实现： 即返回链表中尾指针指向的结点的数据

❗特别注意：

• 需要判断链表此时是否为NULL（空表），如果是则不能返回了

1️⃣返回队尾数据的函数声明：

QDataType QueueBack(Queue* pq);

2️⃣返回队尾数据函数的实现：

QDataType QueueBack(Queue* pq){assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;}

🥐Ⅵ.判断队列是否为NULL

👉简单来说： 就是判断头指针是否指向NULL（空）

➡️实现： 判断头指针的指向即可

1️⃣判断队列是否为NULL的函数声明：

bool QueueEmpty(Queue* pq);

2️⃣判断队列是否为NULL函数的实现：

bool QueueEmpty(Queue* pq){assert(pq);return pq->head == NULL;}

🥐Ⅶ.获取队列结点个数

👉简单来说： 返回队列结点的个数

➡️实现： 即对链表遍历一次即可

1️⃣返回队列结点个数的函数声明：

int QueueSize(Queue* pq);

2️⃣返回队列结点个数函数的实现：

int QueueSize(Queue* pq){assert(pq);int size = 0;QueueNode* cur = pq->head;while (cur){cur = cur->next;size++;}returnsize;}

🥐Ⅷ.队列的销毁

👉简单来说： 对队列进行空间释放

➡️实现： 与链表的销毁操作一样

1️⃣队列的销毁的函数声明：

void QueueDestroy(Queue* pq);

2️⃣队列的销毁函数的实现：

void QueueDestroy(Queue* pq){assert(pq);QueueNode* cur = pq->head;while (cur) {QueueNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;}

🥯Ⅸ.总结

✨综上：就是队列接口实现的内容啦~

➡️相信大家对队列有不一样的看法了吧🧡

---

🫓总结

综上，我们基本了解了数据结构中的 “栈和队列” 🍭 的知识啦~~

恭喜你的内功又双叒叕得到了提高！！！

感谢你们的阅读😆

后续还会继续更新💓，欢迎持续关注📌哟~

💫如果有错误❌，欢迎指正呀💫

✨如果觉得收获满满，可以点点赞👍支持一下哟~✨

创作打卡挑战赛 赢取流量/现金/CSDN周边激励大奖好看字体下载