且为整数

        现实中很多问题都需要求整，下面我们用Matlab来解决这个问题，我们这里使用分支定界法。

先用线性规划解出大致范围。

%初步处理clear allclcc=[40 90];%填目标函数系数a=[9,7;7,20]; %就是要一致大于或小于，然后取条件函数系数b=[56;70];%条件函数已知数部分aeq=[];%若存在一个等式限制，则填写等式系数beq=[];%等式已知数部分lb=[0;0];%没有下限ub=[inf;inf];%没有上限[x,y]=linprog(-c,a,b,aeq,beq,lb,ub);xbest=c*x%计算最优值

 这是我们利用线性规划解出的。

分枝定界法

第一步

根据上一步结果，可以暂定z上限为 356。同样也可以看出当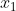,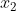分别为0时z最小，最小为0。故最大值z范围可定位。

第二步

先对分枝

4和5之间就没有整数，该方法叫做分枝

约束条件转变

<img alt="0\leq x_1    0" class="mathcode" src="https://latex.codecogs.com/gif.latex?x_2%3E0" />

%整数规划clear allclcc=[40 90];%填目标函数系数a=[9,7;7,20]; %就是要一致大于或小于，然后取条件函数系数b=[56;70];%条件函数已知数部分aeq=[];%若存在一个等式限制，则填写等式系数,没有等式约束，因此aeq,beq都为空beq=[];%等式已知数部分lb=[0;0];%下限依然都为0ub=[4;inf];%x1上限为4，x2没有上限[x,y]=linprog(-c,a,b,aeq,beq,lb,ub);x    %获取对应x1,x2best=c*x%计算最优值

运行结果：

 我们得出,,

换分割的x范围，

  0" class="mathcode" src="https://latex.codecogs.com/gif.latex?x_2%3E0" />

%整数规划clear allclcc=[40 90];%填目标函数系数a=[9,7;7,20]; %就是要一致大于或小于，然后取条件函数系数b=[56;70];%条件函数已知数部分aeq=[];%若存在一个等式限制，则填写等式系数,没有等式约束，因此aeq,beq都为空beq=[];%等式已知数部分lb=[5;0];ub=[inf;inf];[x,y]=linprog(-c,a,b,aeq,beq,lb,ub);x    %获取对应x1,x2best=c*x%计算最优值

运行结果：

 我们得出,,

现在我们可以把最优解再定界，确定范围为：

第三步

对处理，这里不细写。

 因此我们可以再次确定z范围为

第四步

对第二种情况分析

 可以看到，没有解

综合上面两个分枝，第一个仍有小数，不可取；第二个不可行解，也不可取。这样的操作称为剪枝。

 结论

第二种情况，两分枝都不可取，第一种只有一个枝可取，即最优解为：

,,

总结

开始，将要求解的整数规划问题称为问题A,将与它相应的线性规划问题称为问题B。求解情况如下:
1. B没有可行解，这时A也没有可行解，则停止
2. B 有最优解，并符合问题A的整数条件，B 的最优解即为A的最优解，则停止。
3. B有最优解，但不符合问题A的整数条件,记它的目标函数值为z,通过我上述所说的四个步骤使用分枝定界法进行分枝，剪枝,最后得出结果。