首先要理解公共子串和公共子序列

公共子串和公共子序列是两个不相同的概念, 公共子串要求字符连续, 公共子序列不要求字符连续。
比如: 字符串"ascde", “axcxdde”
最长公共子串是 “de” , 因为 "de"在两个字符串中都是连续的
最长公共子序列是 “acde”, 不要求连续, 只要满足两个字符串中子序列前后顺序的一致即可

动态规划求最长公共子序列

动态规划的核心是

• base case
• 状态转移方程
• 自下而上

我们可以通过状态转移表来帮助我们得出状态转移方程
这里我直接说结论:
我们思考一个问题, 如果我们求 字符串 s1的前 i 位子串和 s2的前 j 位子串的最长公共子序列 f(i,j), 跟我们求 s1的前 i-1 位子串和 s2的前 j-1 位子串的最长公共子序列 f(i-1,j-1) 两者之间有什么关系呢?
或者换一种说法, 如果我们知道的 f(i-1,j-1) 的结果 x, 我们如何根据 x 推得 f(i,j) 呢?

其结论就是, 我们判断 s1.charAt(i) 和 s2.charAt(j) 是否相等, 如果相等, 则 f(i,j) = f(i-1, j-1) + 1;
如果不相等, f(i,j) = max(f(i-1, j), f(i, j-1));

这个结论我就不证明了, 这不需要我们开发工程师深入探索。
如果你理解了上面的公式, 我们就可以进入编码阶段。

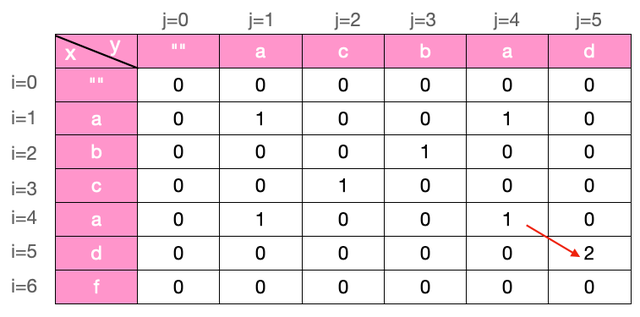
代码实现有两种思路, 一是回溯, 二是动态规划
回溯就是所谓的自上而下, 遇到分支的时候去探索每一个分支, 当遇到末尾的时候回溯到上一分支。动态规划是所谓的自下而上, 先解决子问题, 再根据子问题的结果去解决父问题。动态规划的优势在于, 通过备忘录避免对子问题的重复求解, 缺点和很显然, 用空间换时间, 占用内存。

这里我们用动态规划实现
首先我们需要解决 base case, 我的理解就是边界条件, 也就是 i=0 或者 j=0时的情况

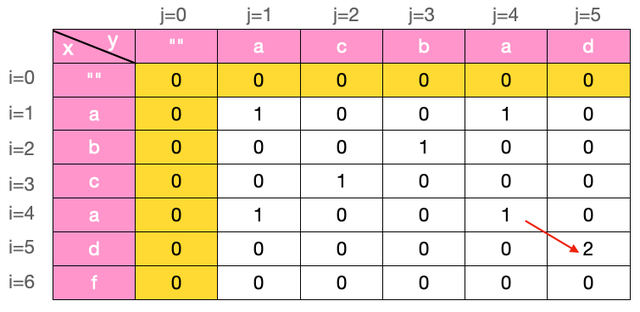
很显然, i=0时, 我们遍历j, 当s1.charAt(i) == s2.charAt(j) 时, f(0,j)=1, j=0时同理

 for (int i = 0; i < s1.length(); i++) {     if (s1.charAt(i) == s2.charAt(0)) {  arr[i][0] = 1;  max = 1;     } } for (int j = 0; j < s2.length(); j++) {     if (s1.charAt(0) == s2.charAt(j)) {  arr[0][j] = 1;  max = 1;     } }

我们把子问题的解缓存到 int[i][j] 的数组arr中, 避免重复求解
整体的题解如下

public class Test2 {    static String s1 = "eabcderfeefx";    static String s2 = "axbcdcxdxeeefx";    public static void main(String[] args) { //最长公共子串 int max = 0; int[][] arr = new int[s1.length()][s2.length()]; for (int i = 0; i < s1.length(); i++) {     if (s1.charAt(i) == s2.charAt(0)) {  arr[i][0] = 1;  max = 1;     } } for (int j = 0; j < s2.length(); j++) {     if (s1.charAt(0) == s2.charAt(j)) {  arr[0][j] = 1;  max = 1;     } } for (int i = 1; i < s1.length(); i++) {     for (int j = 1; j < s2.length(); j++) {  if (s1.charAt(i) == s2.charAt(j)) {      arr[i][j] = arr[i - 1][j - 1] + 1;      max = Math.max(max, arr[i][j]);  } else {      arr[i][j] = Math.max(arr[i][j - 1], arr[i - 1][j]);      max = Math.max(max, arr[i][j]);  }     } } System.out.println(max);    }}

动态规划求最长公共子串

求最长公共子串跟求最长公共子序列是很相似的问题
核心区别就在于 状态转移方程
最长公共子序列问题中我们探索 f(i, j) 和 f(i-1, j-1) 的公共子序列的关系
那么类比到最长公共子串,
你觉得 f(i, j) 和 f(i-1, j-1) 有什么关系呢?

有趣的一点在于, 我们求解最长公共子串时, 要求连续性, 所以 s1.charAt(i) 是否等于 s2.charAt(j), 只能决定特殊情况下 (i,j) 范围 的最长公共子串 和 (i-1, j-1) 范围 的最长公共子串的关系, 那就是这个最长公共子串必须是以 i-1/j-1 结尾的, 那么当 s1.charAt(i)==s2.charAt(j) 时, 才能满足 f(i, j) = f(i-1, j-1) + 1

也就是这里的 f(i, j) 代表的含义是以 i/j 位置为结尾的最长公共子串的长度
而当s1.charAt(i) != s2.charAt(j) 时, f(i, j) = 0

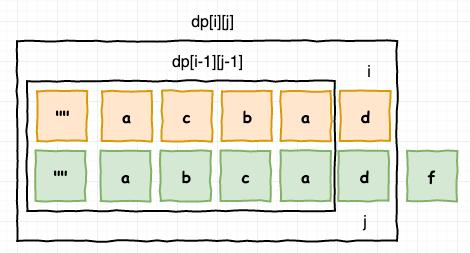
理解了上面的意思, 代码我们几乎不用调整多少
代码如下

public class Test2 {    static String s1 = "eabcderfeefx";    static String s2 = "axbcdcxdxeeefx";    public static void main(String[] args) { //最长公共子串 int max = 0; int[][] arr = new int[s1.length()][s2.length()]; for (int i = 0; i < s1.length(); i++) {     if (s1.charAt(i) == s2.charAt(0)) {  arr[i][0] = 1;  max = 1;     } } for (int j = 0; j < s2.length(); j++) {     if (s1.charAt(0) == s2.charAt(j)) {  arr[0][j] = 1;  max = 1;     } } for (int i = 1; i < s1.length(); i++) {     for (int j = 1; j < s2.length(); j++) {  if (s1.charAt(i) == s2.charAt(j)) {      arr[i][j] = arr[i - 1][j - 1] + 1;      max = Math.max(max, arr[i][j]);  } else {      //最长子串  arr[i][j]代表s1前i为和s2前j位 最长且以最后字符为结尾的公共子串的长度      arr[i][j] = 0;  }     } } System.out.println(max);    }}

空间复杂度优化

根据动态规划的无后效性, 我们可以优化算法的空间复杂度
上面的空间复杂度为 O(m*n), 因为我们记录了整个二维数组, 实际上由于无后效性的特点, 我们只需要记录上一层的结果, 可以将空间复杂度优化为 O(n)

对于各个格子中的数字，它只与其上一行的左上角格子数字有关，与上一行之前的行无关（所以在计算 i = 4 行的格子中，图中 0，1，2 行的格子无需保留），这叫无后效性。

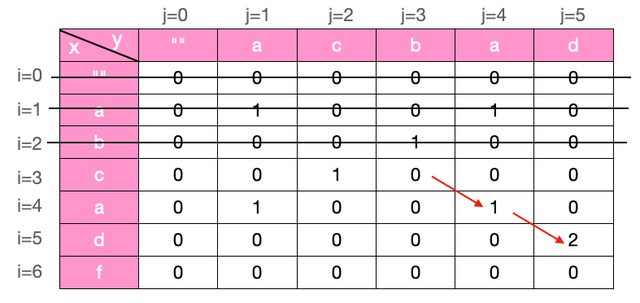
问题变形: 求出最长的公共子串/子序列

到这里, 你可以动手编码试试看。