文章目录

• 前言
• 一、哈希表
• • 1. 分类
  • 2. 什么情况下要用哈希表？
  • 3. 冲突处理
  • • • ① 拉链法
      • • 含义
        • 操作
        • • 插入一个值 x
          • 查找一个值 x
      • ② 开放寻址法
      • • 含义
        • 操作
        • • 插入一个数 x
          • 查找一个数 x
• 哈希表代码实现
• • 1. 模拟散列表
• 二、刷题

前言

        今天算法的内容是：哈希表。
 

一、哈希表

1. 分类

2. 什么情况下要用哈希表？

将一个比较庞大的值域映射到一个比较小的区间（区间范围为 0 ~ N）。

例如，操作数的 个数 是10⁵, 操作数值的 范围 是 -10^9^ ~ 10^9^。在一个比较大的值域里面，从中选出来一些数 插入，选出另一些数 查询，选出来数的个数为 10^5^，能快速的支持 插入 和 查询 这两种操作。

思想：通过一个哈希函数，函数的输入为 x（-10⁹ ~ 10⁹ 值域内的一个数），输出为 0 ~ 10⁵ 的一个数，哈希函数的作用是可以将-10⁹ ~ 10⁹ 值域内的一个数内 映射 到 0 ~ 10⁵ 的一个数。

实现： x $\in$ (-10⁹ ~ 10⁹ )，h 为哈希函数，h(x) $\in$ ( 0 ~ 10⁵ )为哈希值，h(x) = x % 10⁵。

哈希冲突：因为 x 的范围大，不同的 x 可能映射成相同的 y，即将若干不一样的数映射成了同一个数，需要处理冲突 。

3. 冲突处理

① 拉链法

含义

通过一个一维数组来存所有的哈希值，每一个位置都看作是一个 槽 ，将值映射到槽上，每一个槽上都拉一条 链，用来存储当前这个槽上已有的所有的数。

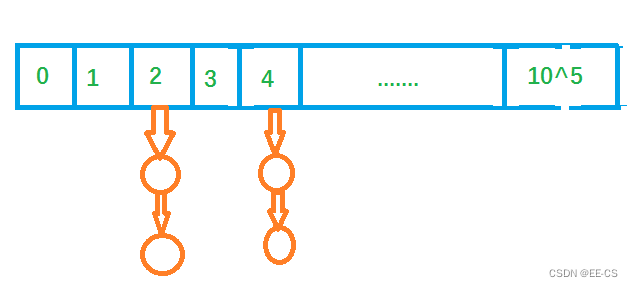
操作

在算法题中哈希表只有 插入 和 查找 这两个操作，操作的时间复杂度都是 O(1)。

插入一个值 x

求 h(x)，h(x) 对应的是哪个槽，将 x 插到这个槽对应的链（单链表）上即可。

查找一个值 x

求 h(x)，看 h(x) 对应的是哪个槽，然后遍历一下这个槽对应的单链表，判断是否存在 x 即可。

② 开放寻址法

含义

开一个一维数组，数组的长度为数据范围的 2 ~ 3 倍，h(x) = k，找到第 k 个位置看其是否有数，如果有就跳到下一个位置，直到找到一个没有数的位置将 x 插入。

操作

插入一个数 x

求 h(x) = k，找到第 k 个位置，然后从第 k 个位置开始往后找，直到找到第一个空的位置为止，然后将 x 插入。

查找一个数 x

h(x) = k，找到第 k 个位置，从第 k 个位置开始从前往后找，每一次先看一下当前位置有没有数，如果当前位置没有数说明 x 不存在，如果当前位置有数并且是 x 的话就证明找到了 x，如果当前位置有数但不是 x，那么往后看下一个位置，以此类推直到找到为止。

find 操作为核心操作。find(x)，如果 x 在哈希表中已经存在的话，返回 x 所在的位置，如果 x 在哈希表中不存在的话，返回的是 x 应该存储的位置。

哈希表代码实现

1. 模拟散列表

AcWing 840. 模拟散列表 原题链接

// 开放寻址法#include #include using namespace std;const int N = 200003, null = 0x3f3f3f3f;int h[N];int find(int x){    int t = (x % N + N) % N;    while (h[t] != null && h[t] != x)    { t ++ ; if (t == N) t = 0;    }    return t;}int main(){    memset(h, 0x3f, sizeof h);    int n;    scanf("%d", &n);    while (n -- )    { char op[2]; int x; scanf("%s%d", op, &x); if (*op == 'I') h[find(x)] = x; else {     if (h[find(x)] == null) puts("No");     else puts("Yes"); }    }    return 0;}

// 拉链法#include #include using namespace std;const int N = 100003;int h[N], e[N], ne[N], idx;void insert(int x){    int k = (x % N + N) % N;    e[idx] = x;    ne[idx] = h[k];    h[k] = idx ++ ;}bool find(int x){    int k = (x % N + N) % N;    for (int i = h[k]; i != -1; i = ne[i]) if (e[i] == x)     return true;    return false;}int main(){    int n;    scanf("%d", &n);    memset(h, -1, sizeof h);    while (n -- )    { char op[2]; int x; scanf("%s%d", op, &x); if (*op == 'I') insert(x); else {     if (find(x)) puts("Yes");     else puts("No"); }    }    return 0;}

二、刷题

LeetCode 1748. 唯一元素的和 原题链接

class Solution {public:    int sumOfUnique(vector<int>& nums) { int sum = 0; vector<int> heap(105, 0); for (auto num : nums) heap[num] ++; for (auto num : nums) {     if (heap[num] == 1)   sum += num; } return sum;    }};

LeetCode 387. 字符串中的第一个唯一字符 原题链接

class Solution {public:    int firstUniqChar(string s) { vector<int> heap(26, 0); for (auto c : s) heap[c - 'a'] ++; for (int i = 0; i < s.size(); i ++) {     if (heap[s[i] - 'a'] == 1)  return i; } return -1;    }};

LeetCode 1941. 检查是否所有字符出现次数相同 原题链接

class Solution {public:    bool areOccurrencesEqual(string s) { vector<int> heap(26, 0); for (auto c : s) heap[c - 'a'] ++; int v = heap[s[0] - 'a']; for (int i = 0; i < 26; i ++) {     if (heap[i] > 0 && heap[i] != v)   return false; } return true;    }};

LeetCode 448. 找到所有数组中消失的数字 原题链接

• 没有空间限制的情况下：开一个长度为 n的 heap数组用来标记 1-n每个数是否出现过，遍历整个 nums数组，标记一下所有出现过的数；之后再从 1-n遍历 heap数组将没有出现过的数输出；
• O(1) 的空间复杂度：对原数组进行修改，如果 x出现过，将 a[x]变成 -a[x]（标记），统计没有改变数的数量；

class Solution {public:    vector<int> findDisappearedNumbers(vector<int>& nums) { for (auto x : nums) {     x = abs(x);     if (nums[x - 1] > 0) nums[x - 1] *= -1; // 没有标记过，进行标记 } vector<int> ret; for (int i = 0; i < nums.size(); i ++) {     if (nums[i] > 0)   ret.push_back(i + 1); } return ret;    }};

LeetCode 1512. 好数对的数目 原题链接

class Solution {public:    int numIdenticalPairs(vector<int>& nums) { vector<int> heap(105, 0); int ans = 0; for (int i = 0; i < nums.size(); i ++) {     ans += heap[nums[i]];     heap[nums[i]] ++; } return ans;    }};