【深度学习】：《100天一起学习PyTorch》模型评估和选择（上）：欠拟合和过拟合

• ✨本文收录于【深度学习】：《100天一起学习PyTorch》专栏，此专栏主要记录如何使用PyTorch实现深度学习笔记，尽量坚持每周持续更新，欢迎大家订阅！
• 🌸个人主页：JoJo的数据分析历险记
• 📝个人介绍：小编大四统计在读，目前保研到统计学top3高校继续攻读统计研究生
• 💌如果文章对你有帮助，欢迎✌关注、👍点赞、✌收藏、👍订阅专栏

参考资料：本专栏主要以沐神《动手学深度学习》为学习资料，记录自己的学习笔记，能力有限，如有错误，欢迎大家指正。同时沐神上传了的教学视频和教材，大家可以前往学习。

• 视频：动手学深度学习
• 教材：动手学深度学习

文章目录

• 【深度学习】：《100天一起学习PyTorch》模型评估和选择（上）：欠拟合和过拟合
• 1.基本概念
• • 1.1训练误差和泛化误差
  • 1.2训练集、验证集和测试集
  • 1.3 交叉验证
  • 1.4模型复杂度
• 2. 多项式回归
• • 2.1 三次多项式回归（正常拟合）
  • 2.2 一元线性回归（underfitting）
  • 2.3 10次多项式（过拟合）
• 3.总结

1.基本概念

机器学习的任务是发现一种泛化的模式，通过训练集发现总体的规律，从而在未知的数据集上也能展现较好的精度。但是如何判断我们的模型不是单纯的记住了数据，而是真的发现了一种规律呢？因为，我们往往只能从有限样本集训练模型，当收集更多的数据时，会发现这些数据的预测结果和之前的关系完全不同。下面我们介绍一些机器学习评估模型的一些基本概念。

1.1训练误差和泛化误差

• 训练误差：模型在训练集上的误差
• 泛化误差：模型误差的期望

在现实情况，我们永远不能准确计算出泛化误差，因此， 在实际中，我们只能通过将模型应用于一个独立的测试集来估计泛化误差。

1.2训练集、验证集和测试集

• 训练集：用于训练模型，得到模型参数
• 验证集：用于选择模型，调整超参数
• 测试集：用于评估模型

在训练数据时，我不希望用到测试集的数据，因为这样的话测试集得到的评估结果是很容易过拟合的。因此我们需要将数据集分为训练集、验证集和测试集，但是在实际应用是，验证集和测试集往往区分的不是很清楚。因此，很多时候，在实际中只设置了训练集和验证集。因此，我们在后续主要关注验证集的误差。

1.3 交叉验证

我们讨论了训练误差和验证误差。我们常常用交叉验证的方法来计算验证误差：

• 留一法交叉验证
  留一法交叉验证，每次将一个样本作为验证集，剩下的n-1个样本作为训练集:(x2 ,y2 ) , . . . , (xn ,yn ) {(x_2,y_2),...,(x_n,y_n)} (x2​,y2​),...,(xn​,yn​)。拟合模型。如下图所示：
  
  我们相当于做了n次模型训练，然后将这n次拟合的平均验证误差来估计某一个具体模型的验证误差。第一次训练得到的验证误差为：M SE1 = (y1 − y ^ 1 )2 MSE_1=(y_1-\hat{y}_1)^2 MSE1​=(y1​−y^​1​)2。重复n次得到：M SE2 , . . . , M SEn MSE_2,...,MSE_n MSE2​,...,MSEn​。最后我们取平均值得到LOOCV估计的测试MSE:

CV ( n ) =1n ∑ i = 1 n M SEi . CV_{(n)}=\frac{1}{n}\sum_{i=1}^{n}MSE_i. CV(n)​=n1​i=1∑n​MSEi​.

• K折交叉验证

K折交叉验证的思路是将数据集随机平均的分为K组。第一组作为验证集，剩下的k-1组作为训练集。当k=n时，留一法交叉验证可以看做是K折交叉验证。和留一法交叉验证类似， M S E 1 MSE_1 MSE1​可以看做是第一次训练时，验证组的平均误差。重复k次，我们可以得到k-折交叉验证的验证误差：
CV ( k ) =1k ∑ i = 1 k M SEi . CV_{(k)}=\frac{1}{k}\sum_{i=1}^{k}MSE_i. CV(k)​=k1​i=1∑k​MSEi​.
下图给出了5折交叉验证的示意图：

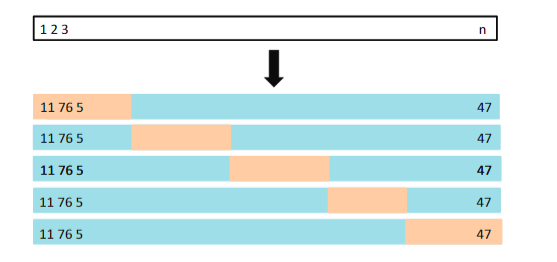
1.4模型复杂度

在得到训练的模型后，计算其训练误差，验证误差。往往会出现两种情况，一种是过拟合，一种是欠拟合

• 欠拟合(underfitting)：欠拟合是指模型在训练集上表现的也不好，模型不能很好的拟合训练集
• 过拟合(overfitting)：模型在训练集上表现很好，但是在测试集上表现的较差
• 正则化(regularization)：正则化可以用于处理过拟合问题

当模型出现欠拟合时候，我们可以考虑使用更复杂的模型来进行训练，当模型过拟合时，需要减少模型的复杂度。具体关系如下图所示：

一般来说，当数据集很多时，使用较复杂的模型；当数据集较少时，使用交简单的模型。
下面我们以多项式回归为例来具体看看这些指标情况

2. 多项式回归

经过上述一些概念的介绍，下面通过一个多项式的具体例子来看一下,首先多项式回归定义如下：
y =β0 +β1 X +β2 X2 +β3 X3 + . . . +βn Xn y = \beta_0 + \beta_1X+\beta_2X^2+\beta_3X^3+...+\beta_nX^n y=β0​+β1​X+β2​X2+β3​X3+...+βn​Xn
==当 β 2 , . . . , β n \beta_2,...,\beta_n β2​,...,βn​都为0时，就是一个简单的一元线性回归，因此高次多项式是可以包含低次多项式回归的。==说明高次多项式模型更复杂。下面我们以一个三次多项式的数据为例，分别拟合不同的多项式回归模型，观察其训练误差和验证误差的情况

import mathimport numpy as npimport torchfrom torch import nnfrom torch.utils import datafrom IPython import display

生成一个模拟数据集，其真实的关系是三次多项式回归

max_degree = 20  # 多项式的最大阶数n_train, n_test = 100, 100  # 训练和测试数据集大小true_w = np.zeros(max_degree)  # 设置wtrue_w[0:4] = np.array([5.1, 1.2, -3.1, 5.1])features = np.random.normal(size=(n_train + n_test, 1))np.random.shuffle(features)poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))for i in range(max_degree):    poly_features[:, i] /= math.gamma(i + 1)  # labels的维度:(n_train+n_test,)labels = np.dot(poly_features, true_w)labels += np.random.normal(scale=0.1, size=labels.shape)

下面将多维数组转换为张量（tensor）

true_w, features, poly_features, labels = [torch.tensor(x, dtype=    torch.float32) for x in [true_w, features, poly_features, labels]]

接下来需要先定义一些基本的函数，大家可以直接下载d2l库导入，在沐神的教材上都有，但是有的时候安装d2l报错，因此如果大家不想安装d2l的话，可以参考一下下面这些函数，大家也可以自己将这些函数写入自己的包中方便导入。

# 定义数据迭代器函数def load_array(data_arrays, batch_size, is_train=True):     """构造一个PyTorch数据迭代器"""    dataset = data.TensorDataset(*data_arrays)#将数据转换为tensor    return data.DataLoader(dataset, batch_size, shuffle=is_train)

# 定义一个类来接收变量class Accumulator:  #@save    """在n个变量上累计"""    def __init__(self, n): self.data = [0.0] * n    def add(self, *args): self.data = [a + float(b) for a, b in zip(self.data, args)]    def reset(self): self.data = [0.0] * len(self.data)    def __getitem__(self, idx): return self.data[idx]

# 定义准确率函数def accuracy(y_hat, y):  #@save    """计算预测正确的数量"""    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: y_hat = y_hat.argmax(axis=1)    cmp = y_hat.type(y.dtype) == y    return float(cmp.type(y.dtype).sum())

# 计算误差函数def evaluate_loss(net, data_iter, loss):  #@save    """评估给定数据集上模型的损失"""    metric = Accumulator(2)  # 损失的总和,样本数量    for X, y in data_iter: out = net(X) y = y.reshape(out.shape) l = loss(out, y) metric.add(l.sum(), l.numel())    return metric[0] / metric[1]

# 训练函数def train_epoch(net, train_iter,loss,updater):    """三个变量，训练损失，训练准确度，样本数"""    net.train()    metric = Accumulator(3)    for X,y in train_iter: y_hat = net(X) l = loss(y_hat,y) if isinstance(updater, torch.optim.Optimizer):#如果是pytorch内置优化器     updater.zero_grad()     l.mean().backward()     updater.step() else:     """自己定义的优化器"""     l.sum().backward()     updater(X.shape[0]) metric.add(float(l.sum()),accuracy(y_hat,y),y.numel())    return metric[0]/metric[2], metric[1]/metric[2]

# 定义坐标轴函数def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):    """设置matplotlib的轴"""    axes.set_xlabel(xlabel)    axes.set_ylabel(ylabel)    axes.set_xscale(xscale)    axes.set_yscale(yscale)    axes.set_xlim(xlim)    axes.set_ylim(ylim)    if legend: axes.legend(legend)    axes.grid()# 定义保存函数def use_svg_display():  #@save    """使用svg格式在Jupyter中显示绘图"""    display.set_matplotlib_formats('svg')

# 定义一个动画绘制类    class Animator:  #@save    """在动画中绘制数据"""    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,   ylim=None, xscale='linear', yscale='linear',   fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,   figsize=(3.5, 2.5)): # 增量地绘制多条线 if legend is None:     legend = [] plt.show() self.fig, self.axes = plt.subplots(nrows, ncols, figsize=figsize) if nrows * ncols == 1:     self.axes = [self.axes, ] # 使用lambda函数捕获参数 self.config_axes = lambda: set_axes(     self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend) self.X, self.Y, self.fmts = None, None, fmts    def add(self, x, y): # 向图表中添加多个数据点 if not hasattr(y, "__len__"):     y = [y] n = len(y) if not hasattr(x, "__len__"):     x = [x] * n if not self.X:     self.X = [[] for _ in range(n)] if not self.Y:     self.Y = [[] for _ in range(n)] for i, (a, b) in enumerate(zip(x, y)):     if a is not None and b is not None:  self.X[i].append(a)  self.Y[i].append(b) self.axes[0].cla() for x, y, fmt in zip(self.X, self.Y, self.fmts):     self.axes[0].plot(x, y, fmt) self.config_axes() display.display(self.fig) display.clear_output(wait=True)    

# 定义训练函数def train(train_features, test_features, train_labels, test_labels,   num_epochs=400):    loss = nn.MSELoss(reduction='none')#设置损失函数为MSE    input_shape = train_features.shape[-1]    # 不设置偏差，因为我们已经在多项式中已经设置好了    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))#定义线性神经网络    batch_size = min(10, train_labels.shape[0])#确定batch    train_iter = load_array((train_features, train_labels.reshape(-1,1)),    batch_size)#训练集    test_iter = load_array((test_features, test_labels.reshape(-1,1))   ,batch_size)#测试集    trainer = torch.optim.SGD(net.parameters(), lr=0.01)#训练集，使用SGD训练模型    animator = Animator(xlabel='epoch', ylabel='loss', yscale='log',xlim=[1, num_epochs], ylim=[1e-3, 1e2],legend=['train', 'test'])#图形相关设置    for epoch in range(num_epochs): train_epoch(net, train_iter, loss, trainer)   if epoch == 0 or (epoch + 1) % 20 == 0:     animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),#计算训练误差并绘制  evaluate_loss(net, test_iter, loss)))#计算测试误差并绘制    print('weight:', net[0].weight.data.numpy())

2.1 三次多项式回归（正常拟合）

因为我们生成的数据集是3次多项式回归得到的，因此使用三次多项式回归拟合结果会很精确

train(poly_features[:n_train, :4], poly_features[n_train:, :4],      labels[:n_train], labels[n_train:])

weight: [[ 5.1068187  1.2157811 -3.1099443  5.064199 ]]

可以看出，随着训练次数的增加，训练误差和验证误差都不断下降到小于0.01，并且验证误差和验证误差基本一致

2.2 一元线性回归（underfitting）

下面我们使用一元线性回归来拟合数据，由于我们知道真实的数据集是三次关系的，此时使用一元线性回归无法进行精确拟合，会导致模型的bias较大，训练误差和验证误差都很大

# 从多项式特征中选择前2个维度，即1和xtrain(poly_features[:n_train, :2], poly_features[n_train:, :2],      labels[:n_train], labels[n_train:])

weight: [[3.8188436 3.0646155]]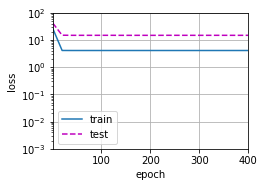

从上图可以看出，和我们预计得到的结果一致，由于模型太简单，连训练集上也不能很好的拟合，导致训练误差和验证误差都很大

2.3 10次多项式（过拟合）

下面我们使用10次多项式来进行拟合，由于模型的复杂度太高，会导致模型出现过拟合，验证集上的误差会随着训练次数增加会先下降再上升

# 从多项式特征中选取所有维度train(poly_features[:n_train, :11], poly_features[n_train:, :11],      labels[:n_train], labels[n_train:], num_epochs=500)

weight: [[ 5.0872297   1.2546227  -2.9732502   4.719495   -0.47507587  1.4278368  -0.05434499  0.30877623  0.28959352  0.18821514  0.06768304]]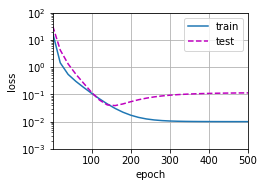

从上图可以看出，和我们预计的一致，验证误差先减小后增大，如果我们提前结束训练的话，能够得到还不错的结果，这种后续中会介绍

3.总结

本章的介绍到此介绍，如果文章对你有帮助，请多多点赞、收藏、评论、关注支持！！