leetcode_Offer51_数组中的逆序对

Offer51_数组中的逆序对

解题思路：利用归并排序

逆序指的是数组中前面元素的 > 后面的元素

而在归并排序的merge操作中，当前面数组的元素 > 后面数组的元素时才合并，因此我们只需要在发生合并的过程中统计一下逆序对的个数

并且只有当两个子数组还存在元素且第一个子数组的元素arr[i] > arr[j]才有可能构成逆序对

且每个arr[j]对应逆序对的个数恰好为第一个数组从i开始到结束的剩余元素个数

统计过程：

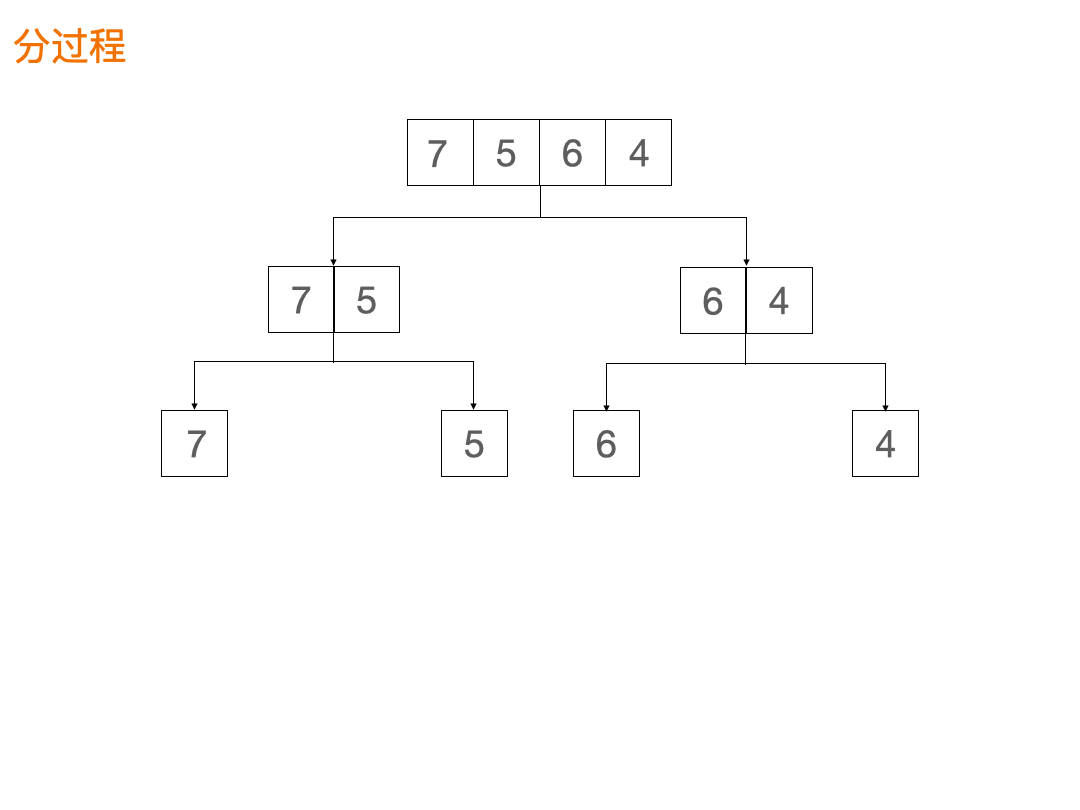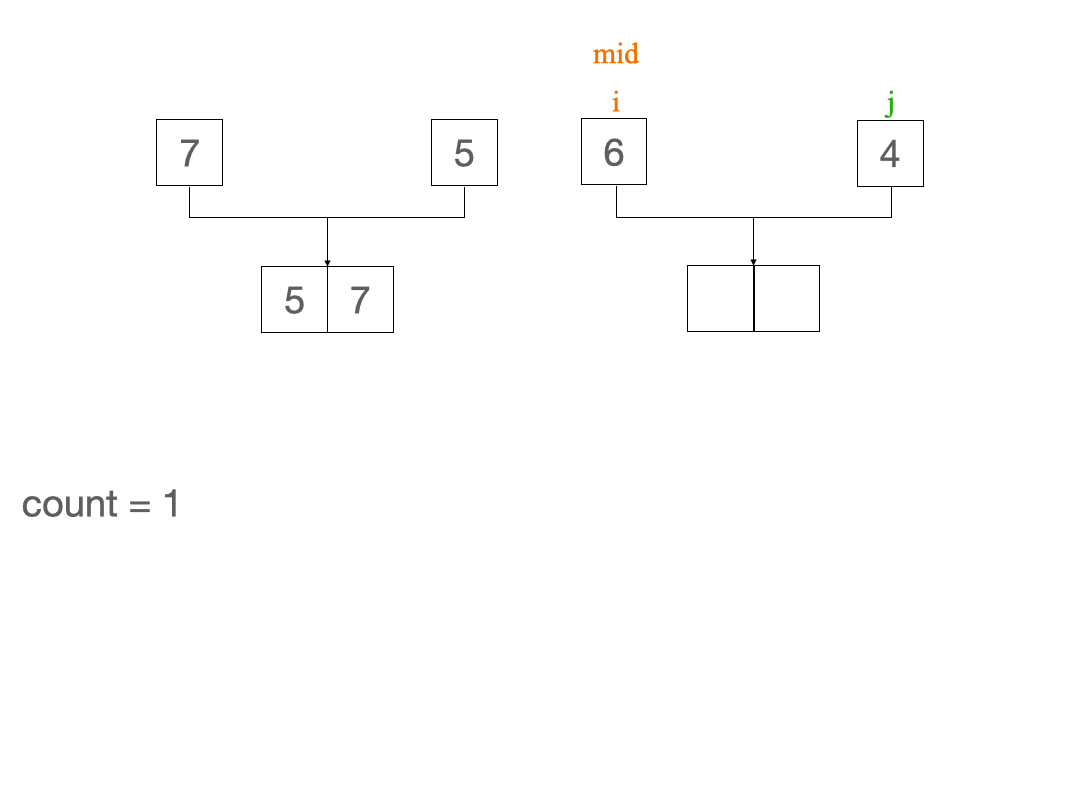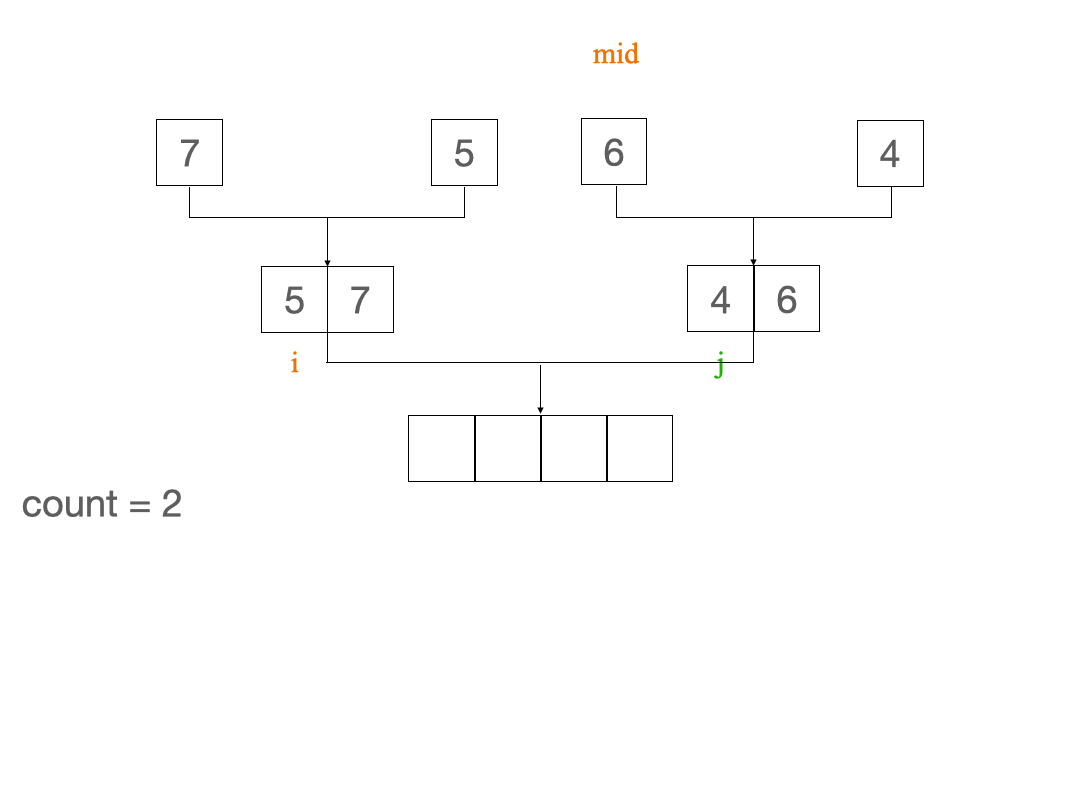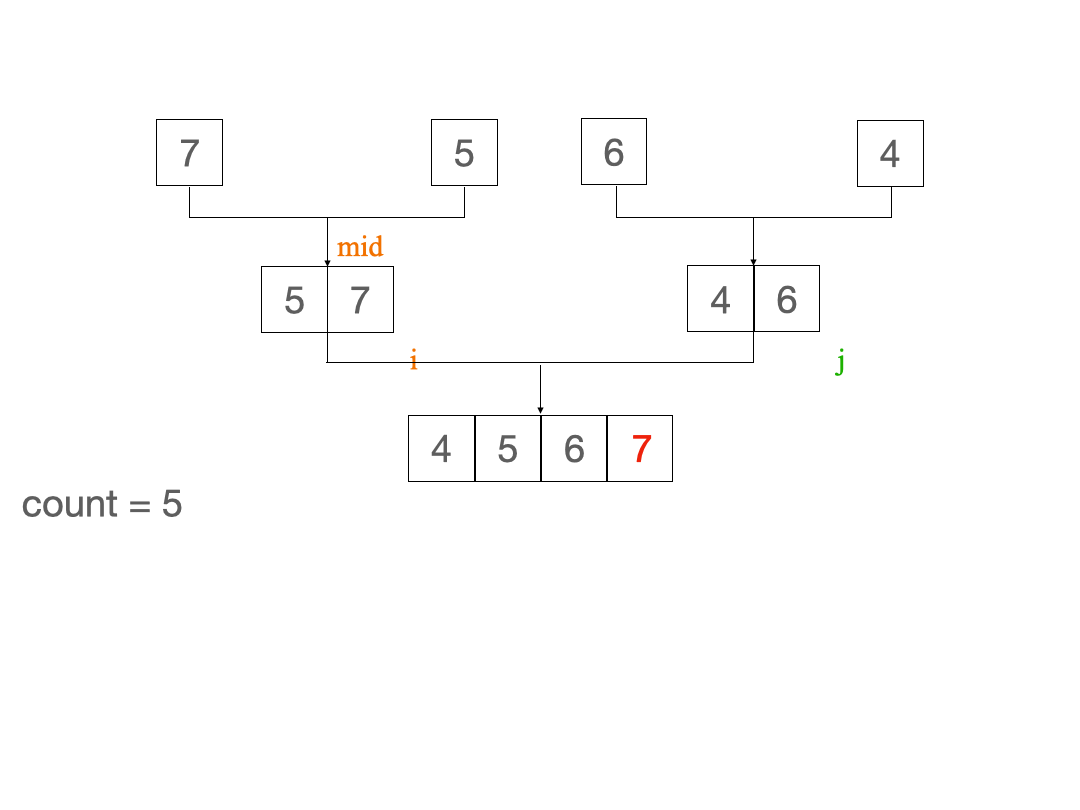
代码示例：

public int Off51_ReversePairs(int[] nums){    return reverseParisInternal(arr, 0, nums.length - 1);}//在数组的[l, r]区间上进行归并排序，返回排序后的逆序对个数private int reverseParisInternal(int[] nums, int l, int r) {    //数组为空或者只有一个元素，一定不构成逆序对    if(l >= r){ return 0;    }    int mid = l + (r - l) / 2;//获得中间位置    //求出两个左右子数组的逆序对个数    int count = reversePairsInternal(nums, l, mid) + reversePairsInternal(nums, mid + 1, r);    //前数组的元素都小于等于后数组的元素时，说明数组有序，因此直接返回count    if(nums[mid] <= nums[mid + 1]){ return count;    }    //当数组还未有序，还存在逆序对    return count += meger(aums, l, mid, r);}//合并两个子数组，返回合并后的逆序对个数private int merge(int[] nums, int l, int mid, int r) {    int[] aux = new int[r - l  + 1];    for(int i = 0; i < aux.length; i++){ aux[i] = nums[i + l];    }    int i = l;    int j = mid + 1;    int count = 0;    for(int k = l; k <= r; k++){ if(i > mid){     //前数组遍历结束     nums[k] = aux[j - l];     j++; }else if(j > r){     //后数组遍历结束     nums[k] = aux[i - l];     i++; }else if(aux[i - l] <= aux[j - l]){     nums[k] = arux[i - l];     i++; }else{     nums[k] = aux[j - l];     count += mid - i + 1;     j++; }    }    return count;}