九日集训day1【刷题】【九日集训】

0.前言 🐱

今天是英雄哥九日集训的第一天，因为白天有事耽搁了，只能晚上回来做一做必做题先了，明天再补上选做题。
今晚打算早点睡，打算明天5点起来看看英雄哥的直播。
不得不佩服，英雄哥是真牛啊，这么早起，太肝了。

1.两整数之和

1. 在不考虑进位的情况下，其无进位加法结果为 a^b
2. 而所有需要进位的位为 a&b 进位后的结果为(a&b) << 1

于是，我们可以将整数 a和 b 的和，拆分为 a 和 b 的无进位加法结果与进位结果的和。

又我们知道有符号整数用补码来表示，所以上述思路也可以推广到 0 和负数。

举个例子：

3：0011 5：0101

1：按位与，左移0 0 1 0需要进位    2：按位异或  0 1 1 0    3：1和2按位与，左移   0 1 0 0 需要进位    4：1和2按位异或      0 1 0 0    5：3和4按位与，左移    1 0 0 0需要进位    6：3和4按位异或  0 0 0 0    7：5和6按位与，左移0 0 0 0无需进位    8：5和6按位异或  1 0 0 0 得到结果为8

class Solution{public:    int getSum(int a, int b)    { while (b) {     int c = ((unsigned int)(a & b)) << 1; //两数相与再左移恰好就是进位的相加     a ^= b;   //两数异或是不进位的相加     b = c; } return a;    }};

2.不用加号的加法

其实就是同一道题哈哈。

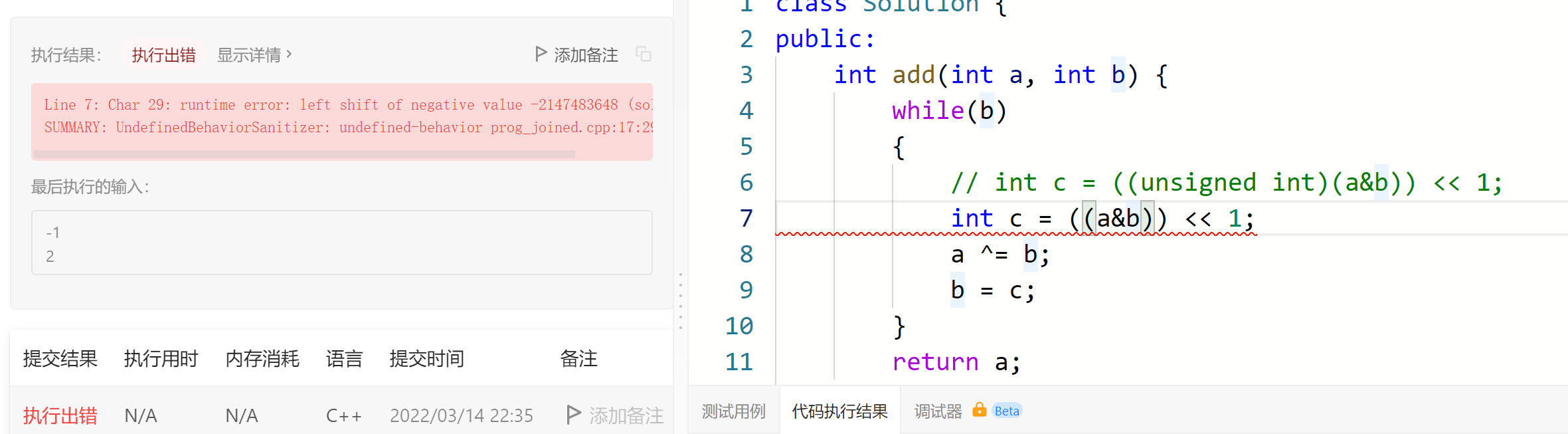
注意

异或之后的结果需要强转成无符号类型，因为力扣上的编译器不支持有符号位左移32位，有符号最高位是符号位。

3.不用加减乘除做加法

依旧是相同的题(#^ . ^#)

4.面试题 08.05. 递归乘法

利用递归，把大问题拆成一个个小问题。

class Solution{public:    int multiply(int A, int B)    { //考虑*0的情况 if (A == 0 || B == 0) {     return 0; } //利用递归，把3*3 拆成 3 + 3*2 return A + multiply(A, B - 1);    }};