两个经典的函数递归问题:青蛙跳台和贝诺塔
前言:对于函数递归,我个人认为算是C语言中难点之一,函数递归的思想就是把大问题转换成小问题-----大事化小;但是有时候这个化解问题的思想却很难把握;下面让我们一起来学习一下函数递归的两个经典问题:青蛙跳台和贝诺塔。并且函数递归一定要有两个必要条件:
1.存在限制条件,当不满足这个限制条件的时候,递归便不再继续;
2.每次递归调用之后越来越接近这个限制条件;函数递归的思想是:大事化小!!并且函数递归有一个回朔的过程。
目录
经典问题一:青蛙跳台
1.解析:
2.具体代码:
3.代码解析:
经典问题二:汉诺塔问题
1.解析:
2.具体代码:
3.代码分析:
经典问题一:青蛙跳台
题目:一只青蛙可以跳上一级台阶,也可以跳上两级台阶。求该青蛙跳上一个n级台阶总共有多少种跳法?
1.解析:
首先我们要在草稿纸上动动笔找一下规律,我们不难发现:
1级台阶:1种跳法==========》1
2级台阶:2种跳法==========》1+1 或 2
3级台阶:3种跳法==========》1+1+1 或 1+2 或 2+1
4级台阶:5种跳法==========》1+1+1+1 或 1+1+2 或 2+1+1 或 1+2+1 或 2+2:
....................................................
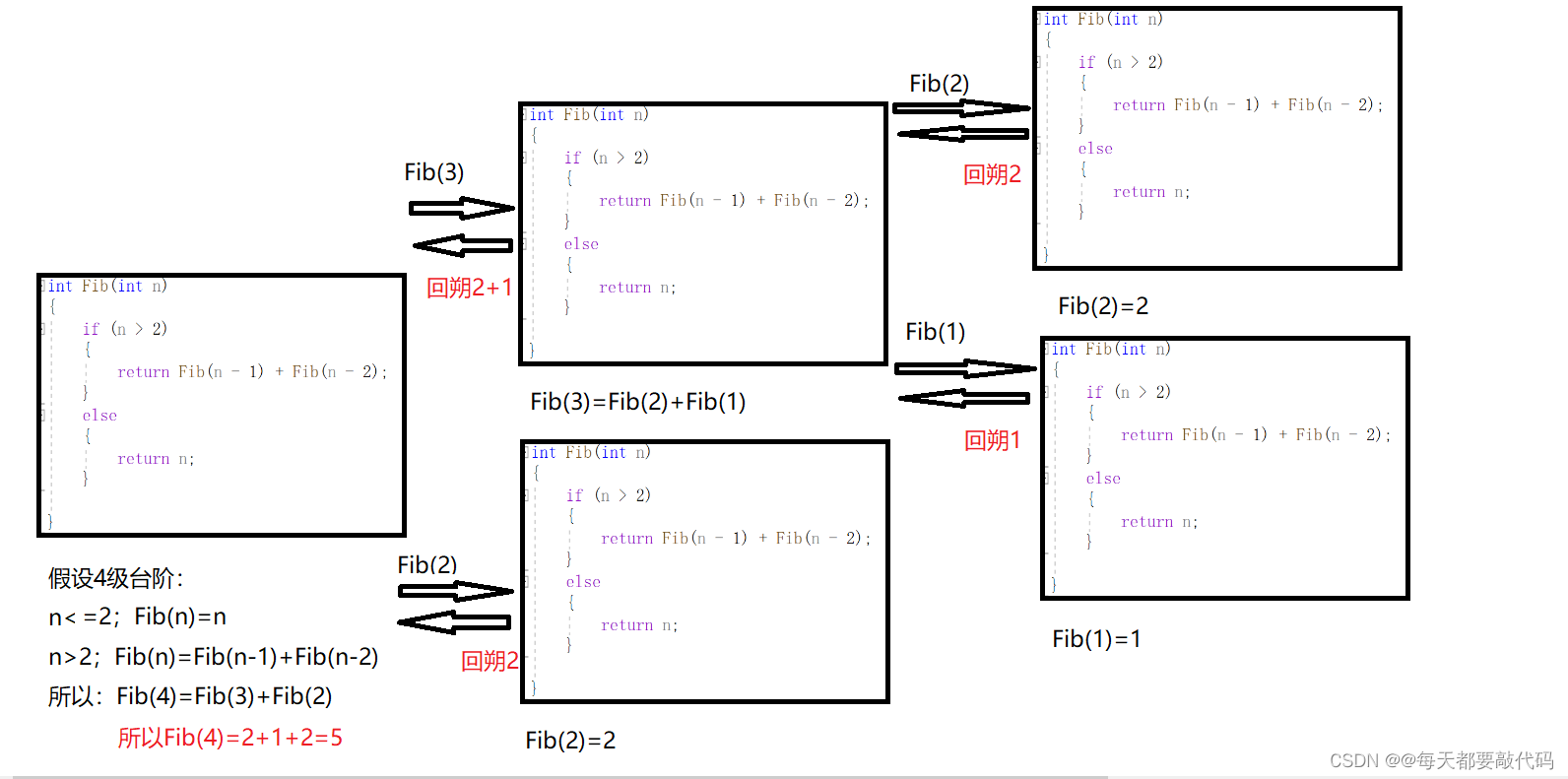
我们多写几组不难发现规律:从3级台阶开始,它跳法的值=前两次跳法值的和;例如:3级跳法数=2级跳法数+1级跳法数;4级跳法数=3级跳法数+2级跳法数...........我们发现,青蛙跳台问题,其实也就是斐波那契数列问题!!!
所以我们就可以写一个函数递归;这个函数名(暂定为Fib);假设有(暂定为n级)台阶;如果n>2;就递归函数Fib(n)=Fib(n-1)+Fib(n-2)====》return Fib(n-1)+Fib(n-2);如果n<=2;就直接return n就可以啦====》因为1级台阶是1种跳法,2级台阶是2种跳法,刚好是对应的。
2.具体代码:

3.代码解析:
有了第一步的解析;我们很容易就能读懂代码,在这里我只说一点:
递归回朔的过程;为了方便,假入为4级台阶:
经典问题二:汉诺塔问题
题目:总共有三个柱子,在一根柱子上,从下往上按照大小顺序摞着n片圆盘。我们需要按大小顺序重新摆放在另一根柱子上。并且规定,在移动过程,小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。假如我们先考虑3片圆盘:
1.解析:
对于汉诺塔问题,我个人觉得思路容易理解,但是如果细思每一个步骤,感觉就很难理解了;所以我现在就是在一种抽象的思维理解它,而不是细思它的每一步挪动;假设有三个柱子分别为:柱子A、柱子B、柱子C;A柱子是起始柱,B是辅助柱,C是终点柱:
假如只有1个圆盘:就可以直接从柱A移动到柱C===》A->C===》移动1次
假如有2两个圆盘:就需要先把最上面小的移动到柱B,再把大的移动到C,最后再把B上的那个小的移动到C===》A->B、A->C、B->C===>移动了3次
假如有3两个圆盘:
1. 就需要先把最上面小的移动到柱C,再把中的移动到B,最后再把C上的那个小的移动到B,再把A上的大的移动到C,通过这个步骤就可以把A柱最下面的大的移动到C柱上;
2. 接下来我们就需要把B柱上的小和中,移动到C柱上,把小移动到A柱,把中移动到C柱;
3. 再把A柱上的小移动到C柱===》A->C A->B C->B A->C B->A B->C A->C===>移动了7次
.........................................................................................
下面的就不在写了,不然我自己都要迷了;这里你可能还是不太明白,所以在代码分析上我会通过画图的方式让你加深理解;我们可以总结一下简单规律,假如有n片圆盘,则需要移动
-1次;这个数字是很庞大的,假如有64个圆盘,你每秒移动一次,那你需要移动多久?不妨自己动手算算,数字大的超乎你的想象!!!
2.具体代码:
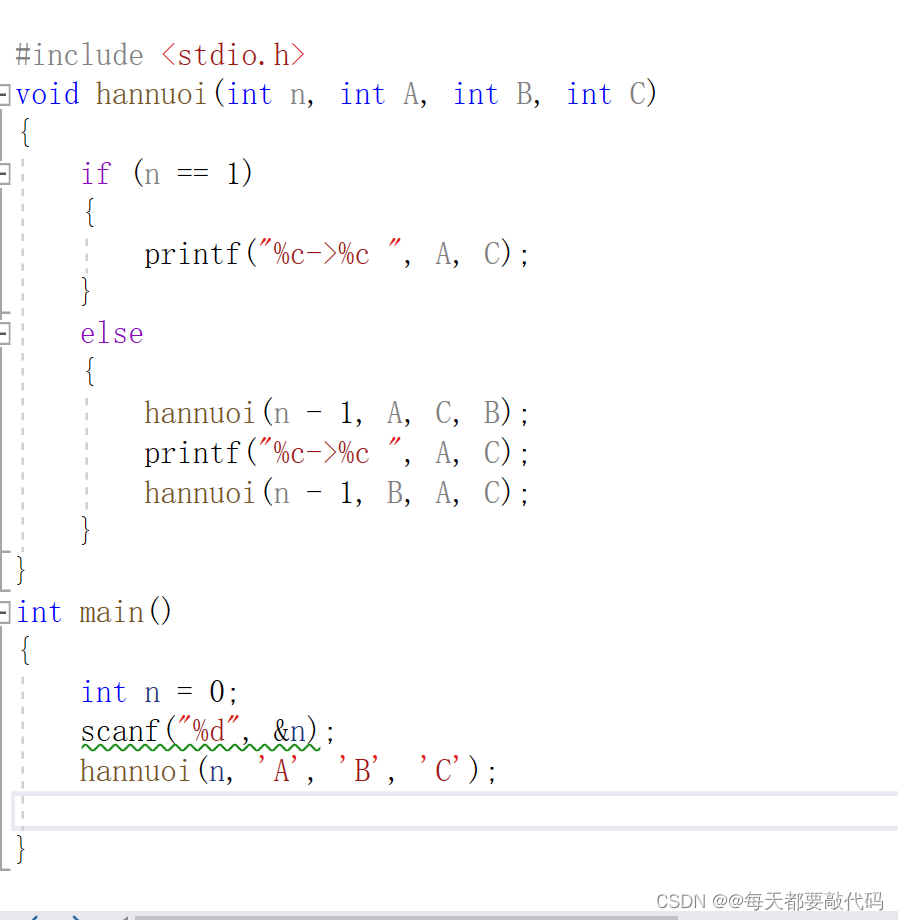
3.代码分析:
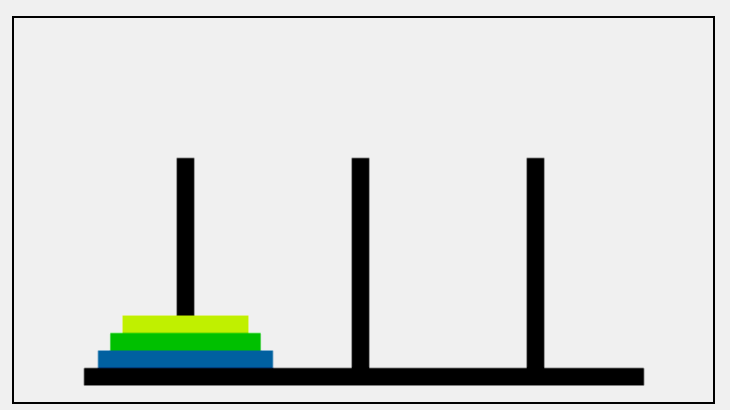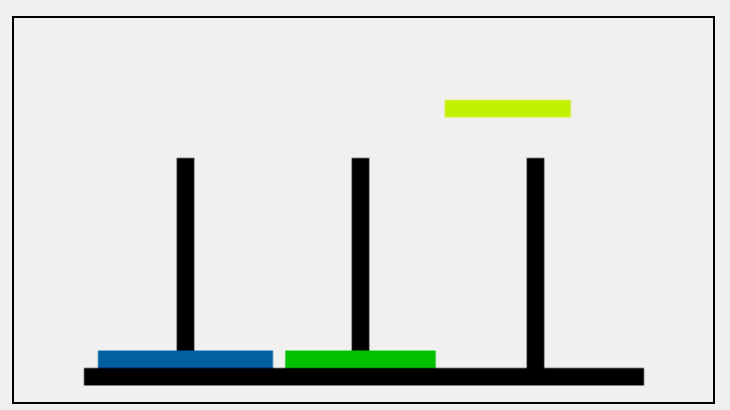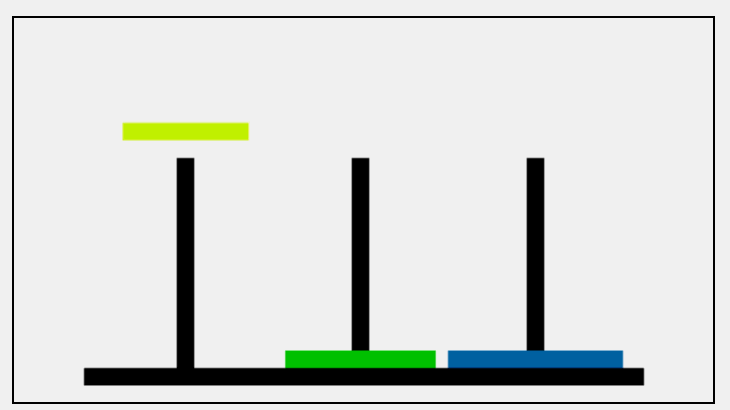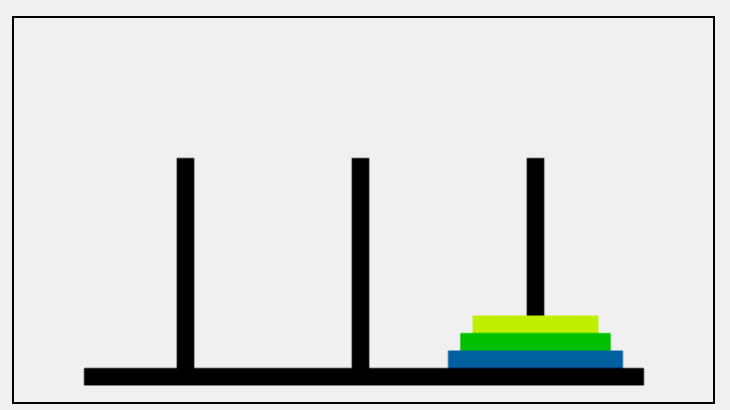
不知道大家发现没有,汉诺塔递归的奥妙所在,假设有三个柱子A、B、C;有三个圆盘为:小、中、大;从上往下看就是从小到大的规律全部都在圆盘A上:
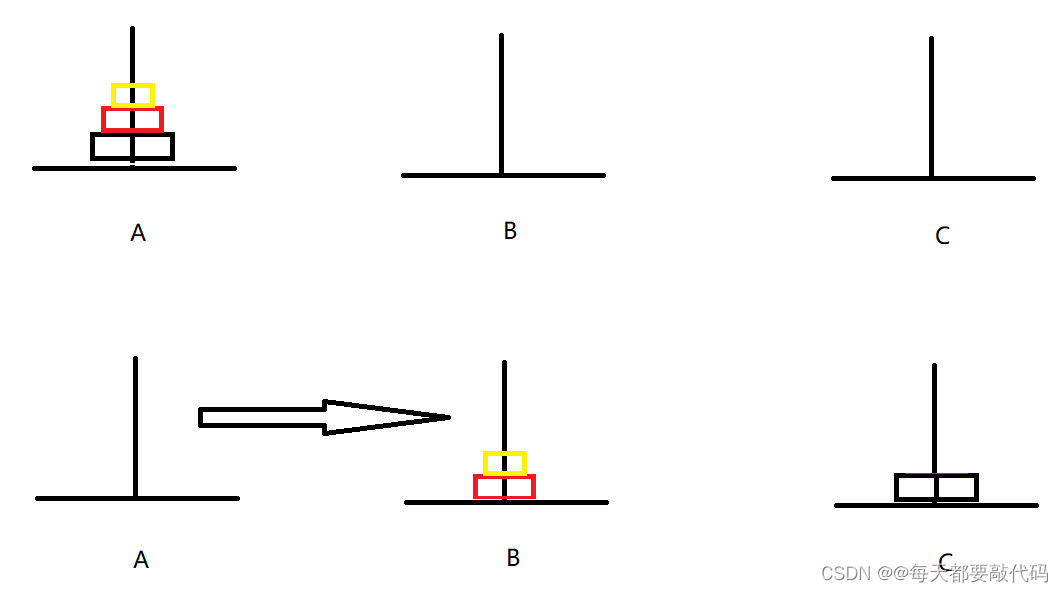
第一步:先把小的移动到C,即A->C;再把中的移动到B,即A->B;再把小的移动到B,即C->B;最后在把大的移动到C,即A->C;第一步结束!!! 总结一下就是A->C A->B C->B A->C;
是不是就相当于把小和中当做一个整体借助C柱移动到B柱,然后把大直接移动到C柱;下面通过图来理解一下:
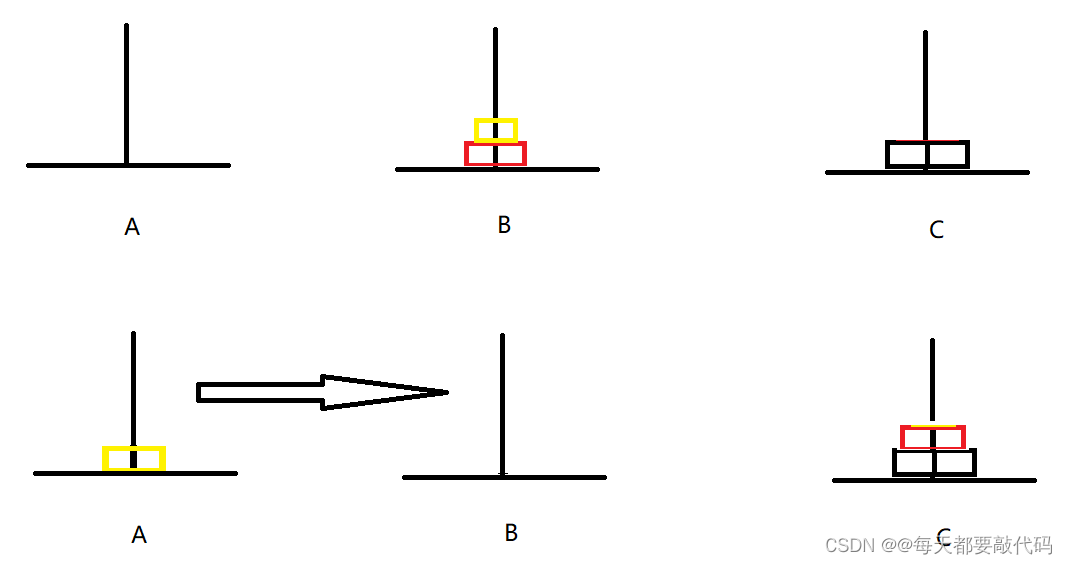
第二步:把B柱上的小中移动到C上,先把小移动到A,即B->A;在把中移动到B,即B->C;总结一下就是B->A B->C;
是不是就相当于把中借助A柱移动到C柱;下面通过图来理解一下:
第三步:就可以把小直接移动到C上就可以啦,即A->C;下面通过图来理解一下:
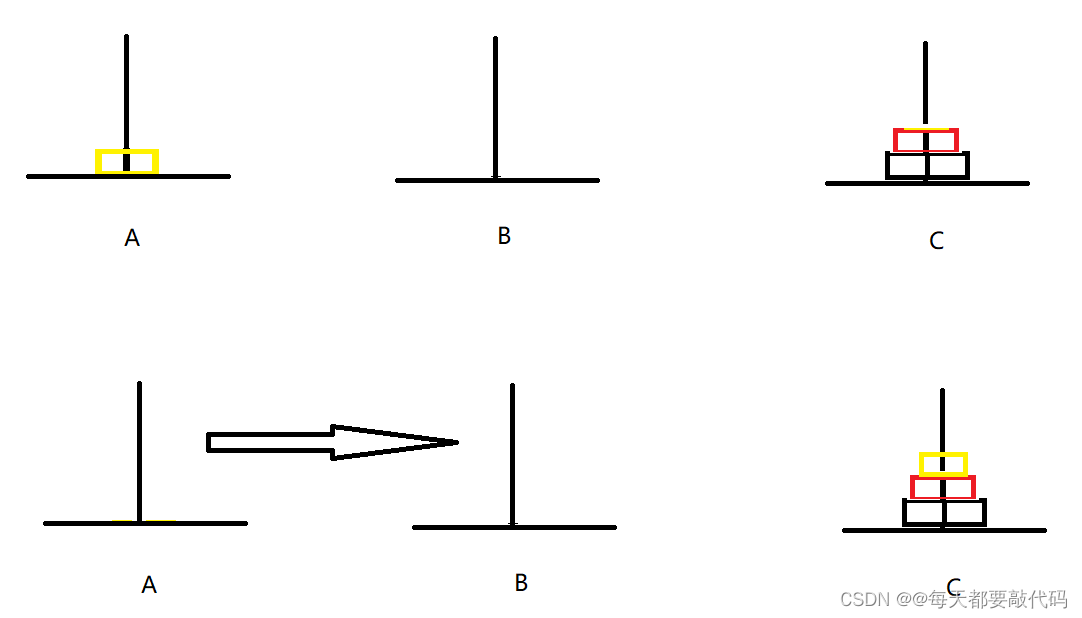
我们会发现汉诺塔的递归主要分为三个步骤:
第一步:需要先判断,如果只有一个圆盘,那么直接从A柱移动到C柱;
第二步:如果n>2;那么直接把n-1个圆盘借助于C柱移动到B柱;在把剩下的一个直接移动到C柱;
第三步:最后在在把B柱上的n-1个圆盘,借助于A柱移动到C柱;

总结:作为函数递归的两个经典例题,我们要多动手画图,分析一下它递归的过程,多刷题,培养这种递归思想,一起加油吧!!!