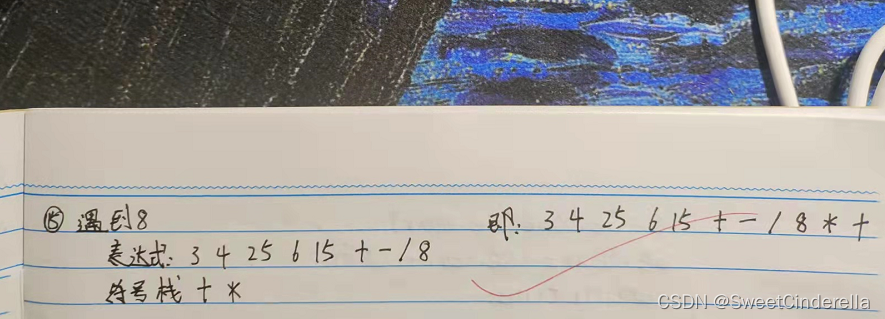中缀表达式转换成后缀表达式知识简介 求3+4/(25-(6+15))*8的后缀表达式
中缀表达式转换成后缀表达式,你是不是也觉得这事儿有点烧脑?别担心,小菜今天来跟你聊聊这个话题!
引言:中缀表达式,就是我们平时写数学题的那个样子,比如"3 + 4 × (2 + 5)"。而把它转成后缀表达式就是要把运算符放在后面,比如"3 4 2 5 + × +"。这看起来好像很简单,但其实要处理运算符的优先级和括号的问题,稍微不注意就会搞砸哦!
相关问题:为什么要转成后缀表达式?是不是有什么好处?
相关答案:好处可多了!首先,计算机处理后缀表达式比中缀表达式方便,因为它不需要考虑运算符优先级和括号的问题。其次,转换过程还能帮助我们理解运算符的优先级规则。比如,加减乘除的优先级是怎么样的,括号又扮演什么角色。
扩展思考:比如,"3 + 4 × (2 + 5)",按照规则,先处理括号里的部分,对吧?那乘法又要在加法之前算。所以,转换后的后缀表达式应该是"3 4 2 5 + × +"。但如果不小心搞错了运算符的顺序,那结果肯定不对哦!
解决办法:记住几个关键词:操作数直接输出,括号特殊处理,运算符按优先级入栈。举个栗子,当遇到左括号(,直接扔进栈里,等到遇到右括号),再把中间的运算符都倒出来。要是遇到运算符,记得比较优先级,低的先出栈!
小彩蛋:如果你觉得转换后的表达式不对,可以再检查一下栈里的运算符顺序。是不是该先出的没出,或者不该出的出错了?比如,遇到加法和乘法,先出乘法对不对?对的,因为乘法优先级高嘛!
中缀表达式转换成后缀表达式
此方法需要遵循几个规则:
(1)如果读入操作数,则直接放入输出字符串;
(2)如果读入一般运算符如+-*/,则放入堆栈,但是放入堆栈之前必须要检查栈顶,并确定栈顶运算符的优先级比放入的运算符的优先级低;如果放入的优先级较低,则需要将栈顶的运算符放入输出字符串;
(3)如果读入(,因为左括号优先级最高,因此放入栈中,但是注意,当左括号放入栈中后,则优先级最低;
(4)如果读入),则将栈中运算符取出放入输出字符串,直到取出(为止,注意:()不输出到输出字符串;
(5)顺序读完表达式,如果栈中还有操作符,则弹出,并放入输出字符串
————————————————
原文链接:https://blog.csdn.net/xiazdong/article/details/7272693
个人理解将中缀表达式转换为算数表达式方法如下:
1,建立符号栈。
2,依次读取每一个数值。
(1)如果是数字直接输出到表达式中;
(2)如果是运算符需要看情况而定。
如果是‘( ’ 直接入栈即可。
如果是‘ )’ 将()中的运算符出栈并输出,两个括号‘()’只出栈不输出。
如果是+-*/等其他符号,入栈后,将前面的符号出栈并输出,直到遇到比当前符号优先级更低的符号或者是‘(’。一入栈若前面的运算符比当前符号优先级更低的符号或者是‘(‘直接入栈当前符号即可。
3,将符号栈中的依次出栈。
引用一个例题:
例 : 3+(2-5)*6/3
遇到 3 是数字输出
表达式 : 3
符号栈 :
遇到”+” 号 , 利用法则iii ,栈中没有优先级更低的符号, 直接入栈
表达式 : 3
符号栈 : +
遇到”(” , 利用 法则i, 直接入栈
表达式 : 3
符号栈 : + (
遇到”2” 输出
表达式 : 3 2
符号栈 : + (
遇到 “-” , 利用法则iii , 遇到”(“, 没有出栈符号, 直接入栈
表达式 : 3 2
符号栈 : + ( -
遇到”5” 输出
表达式 : 3 2 5
符号栈 : + ( -
遇到”)” 利用法则ii , 将”-“号出栈输出, “(” 出栈
表达式 : 3 2 5 -
符号栈 : +
遇到”*” 利用法则ii , “*” 比”+”的优先级低, 所以遇到优先级更低的符号, 不用出栈, 将”*”入栈
表达式 : 3 2 5 -
符号栈 : + *
遇到”6” 输出
表达式 : 3 2 5 - 6
符号栈 : + *
遇到”/” 利用法则ii , “/” 与”*”的优先相同, 就是说”*”不是优先级更低的符号, 所以出栈输出, 继续 “+”比”/”的优先级低, 不用出栈, 将”/”入栈
表达式 : 3 2 5 - 6 *
符号栈 : + /
遇到”3” 输出
表达式 : 3 2 5 - 6 * 3
符号栈 : + /
扫描完成 将符号栈内的符号依次输出
表达式 : 3 2 5 - 6 * 3 / +
————————————————
版权声明:上述例题为CSDN博主「凌波ling」的原创文章
原文链接:https://blog.csdn.net/u012507347/article/details/52245233
求3+4/(25-(6+15))*8的后缀表达式