第十二届蓝桥杯省赛 第一场 C++ B组 题解 (全)
第十二届蓝桥杯
A 空间
问题描述
小蓝准备用 256MB 的内存空间开一个数组,数组的每个元素都是 32 位 二进制整数,如果不考虑程序占用的空间和维护内存需要的辅助空间,请问 256MB 的空间可以存储多少个 32 位二进制整数?
思路:
int,四个字节,不知道可以用sizeof,
1MB=1024KB,1KB=1024B;
code:
#include #define int long long#define rep(i, l, r) for (int i = l; i <= r; ++i)using namespace std;typedef long long ll;const int N = 2e6 + 7;const int mod = 1e9 + 7;signed main() { cout << 256 * 1024 * 1024 / 4 << endl; return 0;}//答案:67108864B 卡片
题目描述:
小蓝有很多数字卡片,每张卡片上都是数字 0 到 9。 小蓝准备用这些卡片来拼一些数,他想从 1 开始拼出正整数,每拼一个,就保存起来,卡片就不能用来拼其它数了。
小蓝想知道自己能从 1 拼到多少。
例如,当小蓝有 30 张卡片,其中 0 到 9 各 3 张,则小蓝可以拼出 1 到 10, 但是拼 11 时卡片 1 已经只有一张了,不够拼出 11。
现在小蓝手里有 0 到 9 的卡片各 2021 张,共 20210 张,请问小蓝可以从 1 拼到多少?
思路:循环暴力,如果当前数不能构成,就结束。
#include #define int long long#define rep(i, l, r) for (int i = l; i <= r; ++i)using namespace std;typedef long long ll;const int N = 2e6 + 7;const int mod = 1e9 + 7;int a[11];void solve() { for (int i = 0; i < 10; i++) { a[i] = 2021; } for (int i = 1; i; i++) { int tmp = i; while (tmp) { if (a[tmp % 10] > 0) a[tmp % 10]--; else { cout << i - 1 << endl; return; } tmp /= 10; } }}signed main() { solve(); return 0;}//3181C 直线
【问题描述】
在平面直角坐标系中,两点可以确定一条直线。如果有多点在一条直线上, 那么这些点中任意两点确定的直线是同一条。
给定平面上2×3个整点{(x,y)|0 ≤ x < 2,0 ≤ y < 3,x ∈ Z,y ∈ Z},即横坐标 是0到1 (包含0和1)之间的整数、纵坐标是0到2 (包含0和2)之间的整数 的点。这些点一共确定了 11 条不同的直线。
给定平面上20×21个整点{(x,y)|0 ≤ x < 20,0 ≤ y < 21,x ∈ Z,y ∈ Z},即横 坐标是0到19 (包含0和19)之间的整数、纵坐标是0到20 (包含0和20)之 间的整数的点。请问这些点一共确定了多少条不同的直线。
思路:一条直线,由斜率和一点就能确定。所以,暴力枚举每两个点算斜率和直线。但是double精度不够导致算得不太一样。
#include using namespace std;set<pair<double, double> > ss; //普通的直线set<double> dx,dy; //两种特殊的直线struct point{ double x, y;};void solve(point a,point b){ if(a.x==b.x) //平行于y轴 dx.insert(a.x); else if(a.y==b.y) //平行于x轴 dy.insert(a.y); else //计算表达式y=kx+bb { double k = (b.y - a.y) / (b.x - a.x); // double bb = a.y - k * a.x; //错误解 double精度丢失 //正解 运用两个点的坐标提升精度 double bb = (a.y * b.x - a.x * b.y) / (b.x - a.x); ss.insert(pair<double, double>(k, bb)); }}int main(){ vector<point> v; for (int i = 0; i <= 19;i++) { for (int j = 0; j <= 20;j++) { point temp = {i * 1.0, j * 1.0};//转换为double v.push_back(temp); } } int len = v.size(); for (int i = 0; i < len;i++) //枚举所有的直线 { for (int j = i + 1; j < len;j++) { solve(v[i], v[j]); } } cout << dx.size() + dy.size() + ss.size(); //三种直线集合个数求和 return 0;}//答案:40257D 货物摆放
【问题描述】
小蓝有一个超大的仓库,可以摆放很多货物。
现在,小蓝有 n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝 规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、 宽、高。
小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上 分别堆 L、W、H 的货物,满足 n = L × W × H。
给定 n,请问有多少种堆放货物的方案满足要求。
例如,当 n = 4 时,有以下 6 种方案:1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 × 1 × 1。
请问,当 n = 2021041820210418 (注意有 16 位数字)时,总共有多少种
思路:
就是找三个因子相乘会等于 给定的数,先预处理所有的因子,然后枚举所有因子,满足则ans++。
code:
#include #define sc(x) scanf("%lld", &(x))#define pr(x) printf("%lld\n", (x))#define rep(i, l, r) for (int i = l; i <= r; ++i)using namespace std;typedef long long ll;const int N = 1e5 + 7;const int mod = 1e9 + 7;#define int long longsigned main() { vector<ll> arr; ll n=2021041820210418; for(ll i=1;i<=n/i;i++){ if(n%i==0){ if(i*i!=n) arr.push_back(i),arr.push_back(n/i); else arr.push_back(i); } } cout<<arr.size()<<endl; int len=arr.size(); int ans=0; for(int i=0;i<len;i++){ for(int j=0;j<len;j++){ for(int k=0;k<len;k++){ if(arr[i]*arr[j]*arr[k]==n) ans++; } } } cout<<ans<<endl;}//2430E 路径
【问题描述】
小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图 中的最短路径。
小蓝的图由 2021 个结点组成,依次编号 1 至 2021。
对于两个不同的结点 a, b,如果 a 和 b 的差的绝对值大于 21,则两个结点 之间没有边相连;如果 a 和 b 的差的绝对值小于等于 21,则两个点之间有一条 长度为 a 和 b 的最小公倍数的无向边相连。
例如:结点 1 和结点 23 之间没有边相连;结点 3 和结点 24 之间有一条无 向边,长度为 24;结点 15 和结点 25 之间有一条无向边,长度为 75。
请计算,结点 1 和结点 2021 之间的最短路径长度是多少。
思路:
这个题目采用的Dijkstra算法求最短路的问题。2021个节点,边权为最小公倍数。
最小公倍数:
a 和 b 的最小公倍数 lcm(a,b)=a*b/gcd(a,b);
Dijkstra算法采用邻接矩阵的方式存图,dist[i] 表示 1 节点到 i 节点的最短路距离。
int dijkstra() { memset(dist, 0x3f, sizeof dist); dist[1] = 0; // 将 1 号点的距离初始化为 0 for (int i = 0; i < n; i++) { int t = -1; // t = -1 表示还没有确定 for (int j = 1; j <= n; j++) { if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j; } st[t] = true; // 将 t 加入到当前已确定最短距离的点的集合中 // 用 t 更新其出边所到达的点到源点的最短距离 for (int j = 1; j <= n; j++) { dist[j] = min(dist[j], dist[t] + g[t][j]); } } if (dist[n] == 0x3f3f3f3f) return -1; return dist[n];}Code:
#include#include#includeusing namespace std;const int N = 2030;int g[N][N];int dist[N];bool st[N];int gcd(int m, int n) {return n ? gcd(n, m % n) : m;}int dijkstra() {memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < 2021; i++) {int t = -1;// 找出距离源点最近的点 for (int j = 1; j <= 2021; j++) {if (!st[j] && (t == -1 || dist[j] < dist[t])) t = j;}st[t] = true;// 遍历 t 的所有出边for (int j = 1; j <= 2021; j++) {dist[j] = min(dist[j], dist[t] + g[t][j]);} }return dist[2021];}int main() {memset(g, 0x3f, sizeof g);for (int i = 1; i <= 2021; i++) {for (int j = 1; j <= 2021; j++) {if (i != j && j - i <= 21) g[i][j] = i * j / gcd(i, j); }}cout << dijkstra() << endl;return 0;}//答案:10266837F 时间显示
【问题描述】
小蓝要和朋友合作开发一个时间显示的网站。在服务器上,朋友已经获取 了当前的时间,用一个整数表示,值为从 1970 年 1 月 1 日 00:00:00 到当前时 刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。小蓝不用显示出年月日,只需要 显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
思路:
水题,随便写写就行了。1s=1000ms;
对3600取模,对60取模。
#include #include #include using namespace std;typedef long long LL;int main(){ LL n; cin >> n; n /= 1000; n %= 86400; int h = n / 3600; n %= 3600; int m = n / 60; int s = n % 60; printf("%02d:%02d:%02d\n", h, m, s); return 0;}G 砝码称重
【问题描述】
你有一架天平和 N 个砝码,这 N 个砝码重量依次是 W1, W2, · · · , WN。 请你计算一共可以称出多少种不同的重量? 注意砝码可以放在天平两边。
思路:
动态规划,线性DP。
状态表示:
d p [ i ] [ j ] dp[i][j] dp[i][j] 表示从前i个中选,称出重量为 j 的方案数。
递推方程:
第 j 个物品有三种选择,不选,选择放入左边,选择放入右边。
dp[i][j]=dp[i-1][j]||dp[i-1][abs(j-w)]||dp[i-1][j+w];Code:
#include using namespace std;const int N = 110, M = 2e5 + 10;int sum;int n;int w[N];bool f[N][M];int main() { cin>>n; for (int i = 1; i <= n; i++) { scanf("%d", &w[i]); sum+=w[i]; } f[0][0]=true; for (int i = 1; i <= n;i++) for (int j = 0; j <=sum;j++) f[i][j]=f[i-1][j]||f[i-1][j+w[i]]||f[i-1][abs(j-w[i])]; //只要有一个非空,f[i][j]就非空 int ans = 0; for (int i = 1; i <=sum;i++) if(f[n][i])ans++;//不为零说明可以选出这个质量的砝码 cout << ans; return 0;}H 杨辉三角形
【问题描述】
下面的图形是著名的杨辉三角形:
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下 数列:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, …
给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
思路:
找规律题。
组合数和杨辉三角:第i行第j列的数都是组合数C(i, j) (i,j从0开始)
C(n, 1) = n --> 对应从左向右看斜着的第二列! —> 一定有解
由于杨辉三角左右对称(C(a, b) == C(a, a-b)),又由于找第一次出现,因此一定在左边,右边可以直接删掉!
1 ---> C(0, 0) 1 1 2 ---> C(2, 1) 1 3 ---> C(2n, n) 1 4 6 ---> C(4, 2) 1 5 101 6 15 20 ---> C(6, 3) n最大1e9,C(34, 17) > 1e9, C(32, 16) < 1e9,因此只要枚举前16个斜行即可! 性质:
每一斜行从上到下递增
每一横行从中间到两边依次递减
因此我们直接从中间对称轴倒序二分找起即可!
C(r, k)对应第 (r + 1) * r / 2 + k + 1 个数
code:
#include #include #include using namespace std;typedef long long LL;int n;LL C(int a, int b)//暴力计算组合数{ LL res = 1; for (int i = a, j = 1; j <= b; i --, j ++ ) { res = res * i / j; if (res > n) return res; } return res;}bool check(int k){ LL l = k * 2, r = max((LL)n, l); while (l < r)//斜行二分, { LL mid = l + r >> 1; if (C(mid, k) >= n) r = mid; else l = mid + 1; } if (C(r, k) != n) return false;//找不到下一行 cout << r * (r + 1) / 2 + k + 1 << endl;//找到输出 return true;}int main(){ cin >> n; //枚举每一斜行 for (int k = 16; ; k -- ) if (check(k)) break; return 0;}I 双向排序
【问题描述】

思路:
算法:栈 + 找规律
这题也是思维题,赛后找规律才找出来,不需要用线段树或者 SplaySplay,只用一个栈也可以写
如果暴力用 sortsort 的话会超时
假设这是我们的原序列

优化一: 由于一开始的序列是升序的,所以如果一开始的操作是后缀操作的话是没有意义的,序列是不会改变的,所以我们从前缀操作开始看,红色为将要操作的前缀序列

如果有连续的前缀操作,我们发现只需要进行最长的一个前缀操作即可,因为短的前缀操作后,长的还是要进行操作,为何不直接进行最长的前缀操作呢,后缀操作同理,我们把所有的操作节点存进栈,有两个成员变量,一个是当前操作是前缀操作还是后缀操作,另一个是操作的边界
优化二: 若进行到下图这种情况时
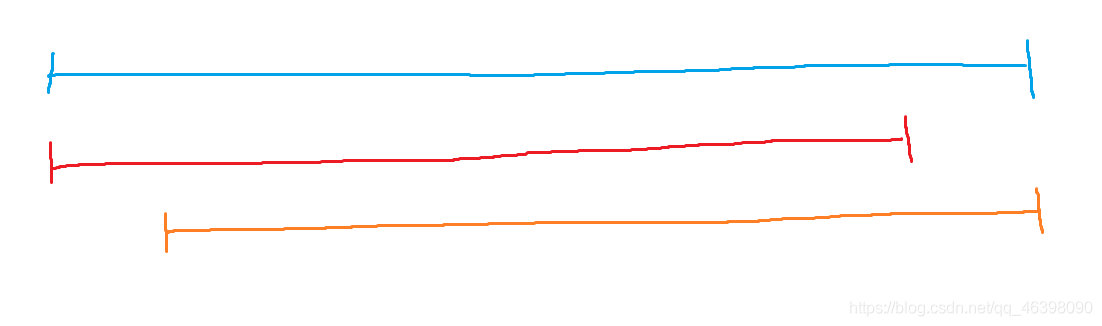
蓝色为原序列,红色为最长连续前缀,橙色为最长连续后缀
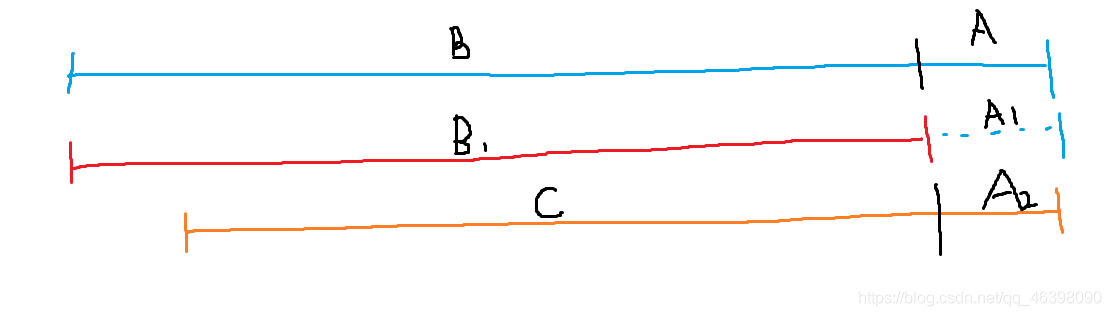
从下图我们发现
- 原序列 A 段严格大于 B 段
- A 段 == A1 段, B 段 == B1 段
- 所以 A1 段严格大于 B1 段
- A2段 == A1 段
- 所以 A2 段严格大于 C 段,所以后缀升序操作(橙色)只需要操作 C 段即可
对于前缀操作同理 ,只需要操作 C 段即可
优化三: 当出现下面这种情况时
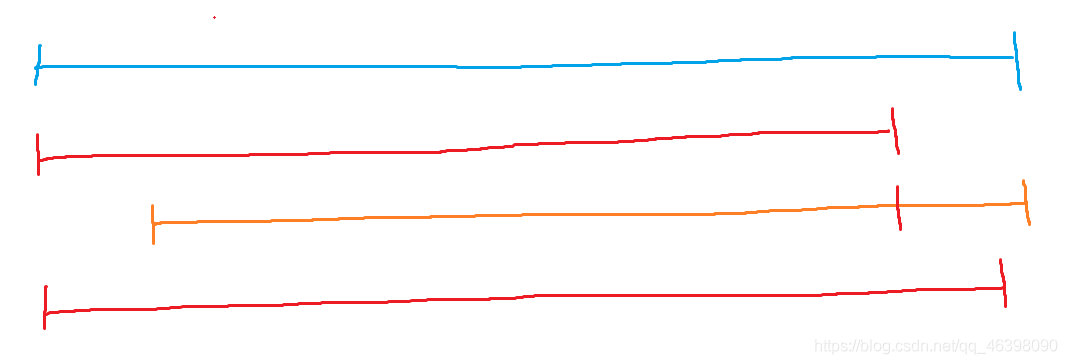
也就是在进行一次前缀操作和后缀操作后,下一次的前缀操作在上一次的前缀操作的节点后,这个时候我们可以把前两次操作给删去,直接进行这一次的前缀操作,因为上一次的后缀操作和前缀操作都包含在了这一次的前缀操作内,前两次操作等于是没用的,所以我们只需要保留当前操作即可
另外,我们可以发现在我们一次次操作的过程中,操作的区间是在慢慢变小的,每次操作的时候,序列总有一部分是不需要进行操作的,我们也就可以用一个变量来递减的填入数组中
暂时还没理解透,存一个代码:
#include #include #include #define x first#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 100010;int n, m;PII stk[N];int ans[N];int main(){ scanf("%d%d", &n, &m); int top = 0; while (m -- ) { int p, q; scanf("%d%d", &p, &q); if (!p) { while (top && stk[top].x == 0) q = max(q, stk[top -- ].y); while (top >= 2 && stk[top - 1].y <= q) top -= 2; stk[ ++ top] = {0, q}; } else if (top) { while (top && stk[top].x == 1) q = min(q, stk[top -- ].y); while (top >= 2 && stk[top - 1].y >= q) top -= 2; stk[ ++ top] = {1, q}; } } int k = n, l = 1, r = n; for (int i = 1; i <= top; i ++ ) { if (stk[i].x == 0) while (r > stk[i].y && l <= r) ans[r -- ] = k -- ; else while (l < stk[i].y && l <= r) ans[l ++ ] = k -- ; if (l > r) break; } if (top % 2) while (l <= r) ans[l ++ ] = k -- ; else while (l <= r) ans[r -- ] = k -- ; for (int i = 1; i <= n; i ++ ) printf("%d ", ans[i]); return 0;}