NC234866 缆车 （思维，图论，最近公共祖先）

传送门：登录—专业IT笔试面试备考平台_牛客网

题目描述

牛妹：“冬天到了，我们一起去坐缆车吧！”

景区有  n个景点，入口在编号为 1 的景点的位置，景区内有  单向缆车，从编号为 1 的景点可以通过缆车到达任意一个其它的景点。

具体来说所有景点中的道路形成了一个树状结构，树根则是编号为 1 的景点，每条树边都是从父亲指向儿子的单向边。

景区改造开始了，景区现在的管理员牛牛规划出了  个结点用于改造，它将指定一个景点  作为去向这  个景点的中转景点（当然，中转景点本身也可能处在这待改造的  个景点中），景区领导打算投资新建一条单向缆车路线使得从景点  出发可以到达这  个景点，要求从  开始 分别 去向规划出的  个景点中的每一个的乘坐缆车数量的和最小，现在需要你帮牛牛计算新建一条缆车之后出从中转点出发最小的乘坐缆车数量和是多少。

输入描述:

第一行一个整数  代表景点个数。

接下来  - 1 行每行两个整数  代表有一条从景点  驶向景点  的有向缆车路线。

接下来一行两个整数   代表规划出的景点个数以及指定的中转景点。

接下来一行  个整数代表规划出的景点编号。

保证输入数据形成一颗树。

     景区编号 

输出描述:

一行一个整数代表最小的从中转点去向选定  个景点的乘坐缆车数量的和。

示例1

输入

复制10 1 2 1 4 1 3 2 5 7 8 8 10 2 7 3 6 6 9 4 7 5 8 6 4

101 21 41 32 57 88 102 73 66 94 75 8 6 4

输出

复制9

9

说明

图形如下：

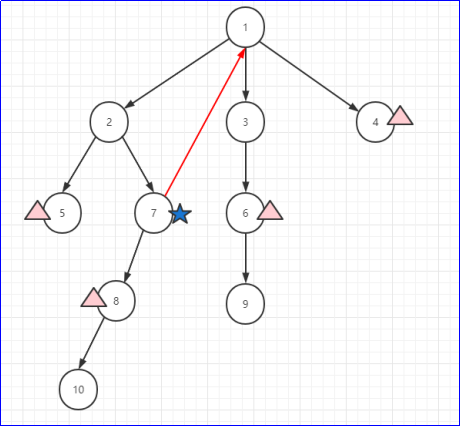
添加如图所示红线后便使得每个 集合内的点通过中转点（这里是点7）后可以到达且游览总和最小。

路径共有四条：

7 -- 1 -- 2 -- 5

7 -- 8

7 -- 1 -- 3 -- 6

7 -- 1 -- 4

所以使用缆车和为：3 + 1 + 3 + 2 = 9。

示例2

输入

复制10 1 2 1 4 1 3 2 5 7 8 8 10 2 7 3 6 6 9 4 6 5 8 6 10

101 21 41 32 57 88 102 73 66 94 65 8 6 10

输出

复制9

9

说明

从点 6 连向点 2 显然最优，总路径长为 9 。

（此例由网友赛后发现的 hack 数据）

 题解：

        题意为让你从星星点到别的点联一条线，使星星点到三角点的距离和最小。

        我们可以分两种情况讨论：

        1：星星点是所有三角点的祖先结点。那么我们直接在星星点的子树遍历一遍，找连线最短的点就行了；减少的距离为该点的三角点个数*（星星点到该点距离-1）（都是单向边）；

        2：不是的话，我们就得找三角点子树外所有点的LCA，然后连一条线，总距离为

sum[星星点]+sum[LCA]+num[LCA] 。

        sum为该点子树内所有三角点到该点的距离。num为该点子树内三角点的个数。

ps：这里用了题解的偷懒lca，按照定义O(n)求得，其实可以倍增O(log(n))求，但是我懒得写了。

/*keep on going and never give up*/#includeusing namespace std;#define int long long#define ll long long#define fast std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);inline int read(){    int x=0,k=1; char c=getchar();    while(c'9'){if(c=='-')k=-1;c=getchar();}    while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();    return x*k;}const int maxn=3e5+10;const int mod=998244353;int n,m,k,a[maxn],num[maxn],sum[maxn],dep[maxn];vectore[maxn];void dfs(int now,int fa,int d,bool f){if(f&&now==k) return ;num[now]+=a[now];dep[now]=d;for(auto v:e[now]){if(v==fa) continue;dfs(v,now,d+1,f);num[now]+=num[v];sum[now]+=num[v]+sum[v];}return ;}signed main(){n=read();for(int i=1;i<=n-1;i++){int x1=read(),y1=read();e[x1].push_back(y1);e[y1].push_back(x1);}m=read(),k=read();for(int i=1;i<=m;i++) a[read()]++;dfs(1,0,0,0);if(num[k]==m){//情况一int ma=0;for(int i=1;idep[k]){ma=max(ma,num[i]*(dep[i]-dep[k]-1ll));}}cout<<sum[k]-ma<<endl;}else{//情况二int ans=sum[k],numk=num[k];for(int i=1;i<=n;i++) num[i]=sum[i]=0;dfs(1,0,0,1);int l=-1,md=-1;for(int i=1;imd){md=dep[i];l=i;}}cout<<ans+sum[l]+num[l]<<endl;} return 0^0;}