昨天上课学到的 贪心法
❤写在前面:
❤博客主页:努力的小鳴人
❤系列专栏:算法
❤欢迎小伙伴们,点赞👍关注🔎收藏🍔一起学习!
❤如有错误的地方,还请小伙伴们指正!🌹

目录
- 一、贪心法概述
-
- 🔥实际意义
- 🔥基本思想
- 🔥解题步骤
- 二、会场安排问题
-
- 🔥问题描述
- 🔥算法设计
- 🔥贪心策略
- 🔥算法描述与实现
-
- 👌算法实现
- 🔥算法正确性证明
- 三、单源最短路径问题
-
- 🔥问题描述
- 🔥算法设计
-
- 👌Dijkstra算法思想
- 🔥求解步骤
- 🔥算法实现
一、贪心法概述
贪心法是最接近人们日常思维的一种解题策略
🔥实际意义
简单、直接、高效便是贪心法的三大特点
对于很多相当广泛的问题通常能够产生最优解,就算不能得到问题的最优解,贪心法也能够得到最优解比较好的近似解,进而它在多项式复杂程度的非确定性问题(NP)的求解中的作用越来越重要,近年来在一些竞赛中也常常出现(例:ACM程序设计竞赛),需要参赛选手经过思考得出高效的贪心算法
🔥基本思想
从问题的某一个初始解出发,在每一个阶段都根据贪心策略来做出当前最优的决策,逐步逼近给定的目标,尽可能快地求得更好的解。当达到算法中的某一步不能再继续前进时,算法终止
结论:
每个阶段面临选择时, 贪心法都做出对眼前来讲是最有利的选择
选择一旦做出不可更改,即不允许回溯
根据贪心策略来逐步构造问题的解
🔥解题步骤
- 分解:将原问题分解为若干个相互独立的阶段
- 解决:对于每个阶段依据贪心策略进行贪心选择,求出局部的最优解
- 合并:将各个阶段的解合并为原问题的一个可行解。影响时间复杂性的因素
二、会场安排问题
🔥问题描述
设有n个会议的集合C={1,2,…,n},其中每个会议都要求使用同一个资源(如会议室),而在同一时间内只能有一个会议使用该资源。每个会议i都有要求使用该资源的起始时间bi和结束时间ei,且bi < ei 。如果选择了会议i使用会议室,则它在半开区间[bi, ei)内占用该资源。如果[bi, ei)与[bj , ej)不相交,则称会议i与会议j是相容的。会场安排问题要求在所给的会议集合中选出最大的相容活动子集,也即尽可能地选择更多的会议来使用资源
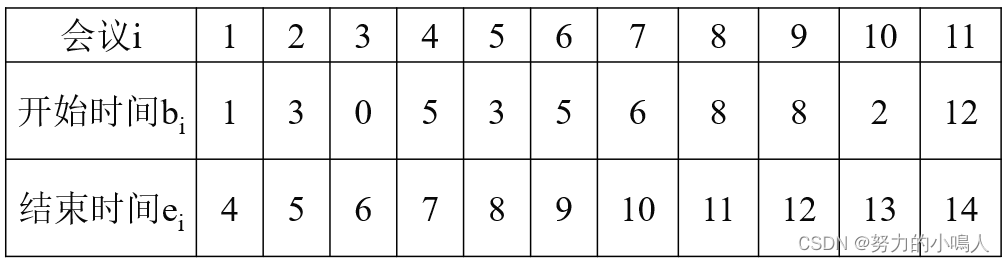
例:
设有11个会议等待安排,用贪心法找出满足目标要求的会议集合
这些会议按结束时间的非减序排列如下表(11个会议按结束时间的非减序排列表):
🔥算法设计
- 步骤1:初始化。开始时间存B;结束时间存E中且按照结束时间的非减序排序,B相应调整;集合A存储解,会议i如果在集合A中,当且仅当A[i]=true;
- 步骤2:根据贪心策略,首令A[1]=true;
- 步骤3:依次扫描每一个会议,如果会议i的开始时间不小于最后一个选入A中的会议的结束时间,则将会议i加入A中;否则,放弃,继续检查下一个会议与A中会议的相容
与上解题步骤对应
🔥贪心策略
选择最早开始时间且不与已安排会议重叠的会议
选择使用时间最短且不与已安排会议重叠的会议
选择具有最早结束时间且不与已安排会议重叠的会议
🔥算法描述与实现
算法描述:时间的数据类型限定为整型
Void GreedySelector(int n,int b[ ],int e[ ],bool A[ ]){ //b中元素按⾮递减序排列,a中对应元素做相应调整; int I,j; C[1]=true; //初始化选择会议的集合C,只包含会议1; j=1;i=2; //从第⼆(i)个会议开始寻找与会议1(j)相容的会议; while(i<=n) if(a[i]>=b[j]) {C[i]=true;j=I;} elseC[i]=false;} 👌算法实现
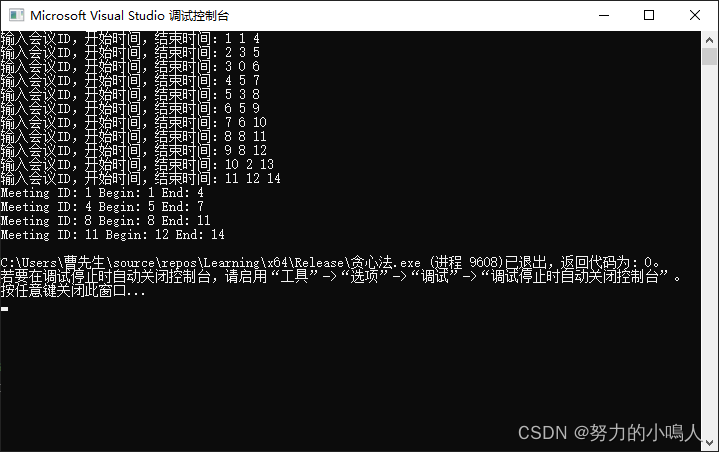
这边我用C实现
#include#pragma warning(disable:4996)#define N 11struct Meeting {int id;int begin;int end;};int main(){Meeting list[N], temp;int k = 0;for (int i = 0; i < N; i++){//输入会议ID,开始时间和结束时间printf("输入会议ID,开始时间,结束时间:");scanf("%d %d %d", &list[i].id, &list[i].begin, &list[i].end);}//Sort meetings according to the end time.for (int i = 0; i < N - 1; i++){for (int j = 0; j < N - i - 1; j++){if (list[j].end > list[j + 1].end){temp = list[j];list[j] = list[j + 1];list[j + 1] = temp;}}}for (int i = 0; i < N; i++){if (i == 0){printf("Meeting ID: %d Begin: %d End: %d\n", list[i].id, list[i].begin, list[i].end);}else{//会议结束的时间尽的可能早if (list[i].begin >= list[k].end){printf("Meeting ID: %d Begin: %d End: %d\n", list[i].id, list[i].begin, list[i].end);k = i;}}}getchar();}例题运行结果:
🔥算法正确性证明
●问题存在从贪心选择开始的最优解
贪心选择性质
采用归纳法
●一步一步的贪心选择能够得到问题的最优解
最优子结构性质
采用反证法
三、单源最短路径问题
🔥问题描述
给定一个有向带权图 G=(V,E),其中每条边的权是一个非负实数。另外,给定V中的一个顶点,称为源点。现在要计算从源点到所有其它各个顶点的最短路径长度,这里的路径长度是指路径上经过的所有边上的权值之和
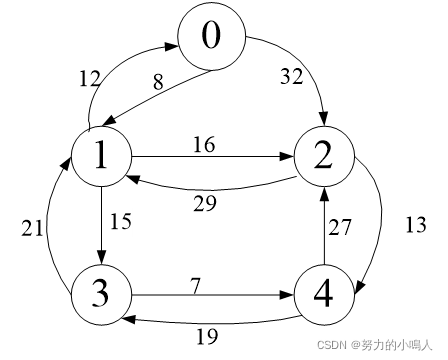
例:
在下图所示的有向带权图中,求源点0到其余顶点的最短路径及最短路径长度
🔥算法设计
- u:源点。集合S中的顶点到源点的最短路径的长度已经确定,集合V-S中所包含的顶点到源点的最短路径的长度待定
- 特殊路径:从源点出发只经过S中的点到达V-S中的点的路径
- 贪心策略:选择特殊路径长度最短的路径,将其相连的V-S中的顶点加入到集合S中
👌Dijkstra算法思想
按各个顶点与源点之间路径长度的递增次序,生成源点到各个顶点的最短路径的方法,即先求出长度最短的一条路径,再参照它求出长度次短的一条路径,依此类推,直到从源点到其它各个顶点的最短路径全部求出为止
🔥求解步骤
- 步骤1:设计合适的数据结构。带权邻接矩阵C,即如果E,令C[u][x]=的权值,否则,C[u][x]=无穷;采用数组dist来记录从源点到其它顶点的最短路径长度;采用数组p来记录最短路径;
- 步骤2:初始化。令集合S={u},对于集合V-S中的所有顶点x,设置dist[x]=C[u][x];如果顶点i与源点相邻,设置p[i]=u,否则p[i]=-1;
- 步骤3:在集合V-S中依照贪心策略来寻找使得dist[x]具有最小值的顶点t,t就是集合V-S中距离源点u最近的顶点
- 步骤4:将顶点t加入集合S中,同时更新集合V-S;
- 步骤5:如果集合V-S为空,算法结束;否则,转步骤6;
- 步骤6:对集合V-S中的所有与顶点t相邻的顶点x,如果dist[x]>dist[t]+C[t][x],则dist[x]=dist[t]+C[t][x]并设置p[x]=t,转步骤3
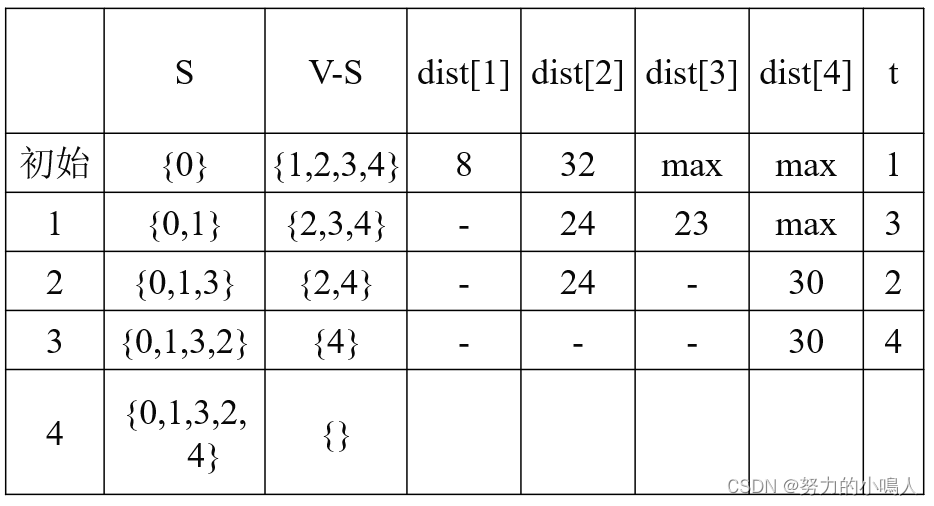
🔥算法实现
Dijkstra迭代过程:
代码实现:
package atCSDN;/ * Description: * Created by 努力的小鸣人 * Date:2022/4/18 * Time:18:17 * 不积跬步,无以至千里 */import java.util.Scanner;public class greedy{ public static void main(String[] args) { Scanner input = new Scanner(System.in); System.out.print("请输入图的顶点和边的个数(格式:顶点个数 边个数):"); int n = input.nextInt(); //顶点的个数 int m = input.nextInt(); //边的个数 System.out.println(); int[][] a = new int[n + 1][n + 1]; //初始化邻接矩阵 for(int i = 0; i < a.length; i++) { for(int j = 0; j < a.length; j++) { a[i][j] = -1; //初始化没有边 } } System.out.println("请输入图的路径长度(格式:起点 终点 长度):"); //总共m条边 for(int i = 0; i < m; i++) { //起点,范围1到n int s = input.nextInt(); //终点,范围1到n int e = input.nextInt(); //长度 int l = input.nextInt(); if(s >= 1 && s <= n && e >= 1 && e <= n) { //无向有权图 a[s][e] = l; a[e][s] = l; } } System.out.println(); //距离数组 int[] dist = new int[n+1]; //前驱节点数组 int[] prev = new int[n+1]; int v =1 ;//顶点,从1开始 dijkstra(v, a, dist, prev); } / * 单源最短路径算法(迪杰斯特拉算法) * @param v 顶点 * @param a 邻接矩阵表示图 * @param dist 从顶点v到每个点的距离 * @param prev 前驱节点数组 */ public static void dijkstra(int v, int[][] a, int[] dist, int[] prev) { int n = dist.length; / * 顶点从1开始,到n结束,一共n个结点 */ if(v > 0 && v <= n) { //顶点是否放入的标志 boolean[] s = new boolean[n]; //初始化 for(int i = 1; i < n; i++) { //初始化为 v 到 i 的距离 dist[i] = a[v][i]; //初始化顶点未放入 s[i] = false; //v到i无路,i的前驱节点置空 if(dist[i] == -1) { prev[i] = 0; } else { prev[i] = v; } } //v到v的距离是0 dist[v] = 0; //顶点放入 s[v] = true; //共扫描n-2次,v到v自己不用扫 for(int i = 1; i < n - 1; i++) { int temp = Integer.MAX_VALUE; //u为下一个被放入的节点 int u = v; //这个for循环为第二步,观测域为v的观测域 //遍历所有顶点找到下一个距离最短的点 for(int j = 1; j < n; j++) { //j未放入,且v到j有路,且v到当前节点路径更小 if(!s[j] && dist[j] != -1 && dist[j] < temp) { u = j; //temp始终为最小的路径长度 temp = dist[j]; } } //将得到的下一节点放入 s[u] = true; //这个for循环为第三步,用u更新观测域 for(int k = 1; k < n; k++) { if(!s[k] && a[u][k] != -1) { int newdist=dist[u] + a[u][k]; if(newdist < dist[k] || dist[k] == -1) {dist[k] = newdist;prev[k] = u; } } } } } for(int i = 2; i < n; i++) { System.out.println(i + "节点的最短距离是:" + dist[i] + ";前驱点是:" + prev[i]); } }}🎁总结:码字动脑不易,三连就是对我最大的支持!
👌 作者算是一名Java初学者,文章如有错误,欢迎评论私信指正,一起学习~~
😊如果文章对小伙伴们来说有用的话,点赞👍关注🔎收藏🍔就是我的最大动力!
🚩不积跬步,无以至千里,书接下回,欢迎再见🌹


