【动态规划】01背包问题+回溯查找背包物品(保姆级、入门级)
目录
一、0-1背包问题
二、问题分析
1、确定备忘录的具体含义
2、状态转移方程
3、初始化
4、遍历顺序及输出
5、回溯法求解最大价值时的背包物品
三、总结
四、完整代码
五、结语
一、0-1背包问题
给定种物品(每种物品均只有一个)和一背包。物品i的重量是
,其价值为
,背包的最大容量为
。怎样选择装入背包中的物品,使得其总价值最大?
例如:现有4种物品,其对应的重量和价值如图所示,另有一最大容量为5的背包,求该背包所能装下物品的最大价值?
| 物品 | 重量 | 价值 |
| 0 | 2 | 4 |
| 1 | 1 | 3 |
| 2 | 4 | 6 |
| 3 | 3 | 5 |
二、问题分析
1、确定备忘录的具体含义
dp[i][j]:任取第0~i件物品,放入容量为j的背包,能得到的最大价值例:dp[1][2]=3的含义:任取物品0~物品1,放入容量为2的背包,能得到的最大价值(取物品1放入背包,其价值最大,为3)dp[i][j] 的定义十分重要,状态方程的书写、数组初始化、遍历顺序和输出结果都必须严格按照该定义进行书写
2、状态转移方程
对于物品,它只有放与不放两种状态,当它能放入背包时,状态转移方程只需取两种状态的最大值; 否则,取不放入时的最大价值。

if (j < w[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);3、初始化
从状态转移方程可知,欲求dp[i][j],需先确定dp[i-1][j]和dp[i-1][j-w[i]]的值(即需保证dp[i][j]的左上角数据已经处理完成),故我们需对第0行和第0列进行初始化.
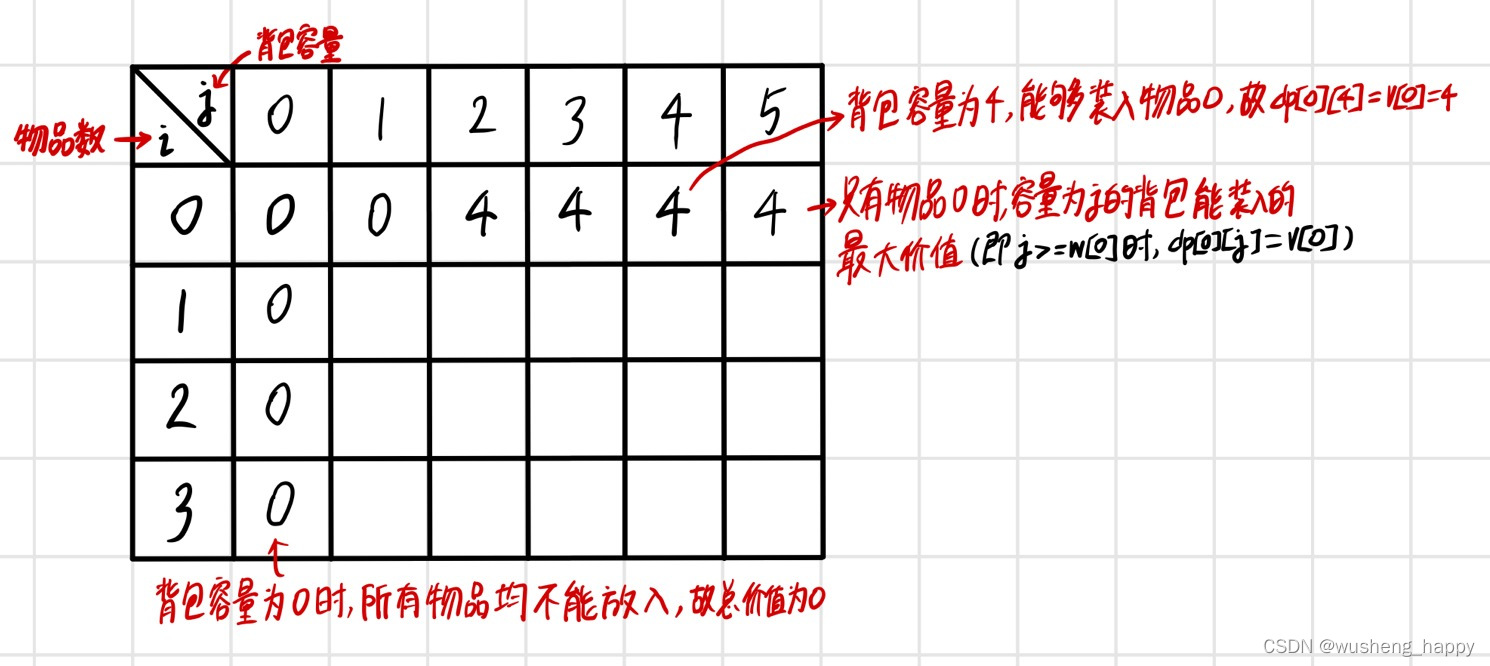
//初始化第0列(即背包容量为0)for (i = 0; i < n; i++)dp[i][0] = 0;//初始化第0行(即只有物品0)for (j = w[0]; j <= max_weight; j++) {if (w[0] <= j) dp[0][j] = v[0];elsedp[0][j] = 0;}4、遍历顺序及输出
遍历顺序:求解dp[i][j]只需提前知道其左上角的数据,故以下两种遍历方式均可。
1、先遍历背包再遍历物品(即物品数固定,背包容量逐增至最大,物品再加1)
2、先遍历物品再遍历背包(即背包容量固定,物品数逐增至最大,背包容量再加1)
输出:dp[n-1][max_weight]: n件物品任取,放入容量为max_weight的背包,所得的最大价值。

//先遍历物品再遍历背包for (i = 1; i < n; i++) { //遍历物品for (j = 1; j <= max_weight; j++) { //遍历背包if (j < w[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);}}//先遍历背包再遍历物品for (j = 1; j <= max_weight; j++) { //遍历背包for (i = 1; i < n; i++) { //遍历物品if (j < w[i])dp[i][j] = dp[i - 1][j];elsedp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);}}5、回溯法求解最大价值时的背包物品
由状态转移方程(dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]))可知,当dp[i][j]dp[i-1][j]时,物品i被放入背包中(判断条件),当dp[i][j]=0时,背包中已经没有物品(结束条件)。

//回溯法求解装入物品i--; j--; //循环结束后,i=n,j=max_weight+1,故使用dp[n - 1][max_weight]须自减1cout << "最大价值时的背包物品为:" <=0) { if (dp[i][j] != dp[i - 1][j]) {cout << "物品" << i << endl;j -= w[i]; //装入物品i后背包的最大容量}i--; //物品i已经处理完成,接下来讨论物品i-1}1、 使用dp[i][j](最大价值)前一定要对i,j进行处理,否则,运行时会抛出异常;
2、结束条件一定要加上i>=0,否则,运行结果可能会出现物品-1等错误。
3、该法得到的结果只为其中的一组最优解,可能还存在其他最优解,例如:当我们装入物品0(2,4)和物品3(3,5)时,其最大价值也为9.
三、总结
1、0-1背包问题是背包问题的基础。深入了解0-1背包问题(每件物品只有一个)是掌握完全背包问题(每件物品有无数个)、多重背包问题(不同物品数量不同)和分组背包(物品分为多组,每组最多选一个)的关键;
2、使用dp[i][j]数组时,一定要注意数组的界限问题,避免越界访问造成错误。比如:刚开始的时候,我认为背包不存在容量为0的情况,故没有将第一列初始化为0,导致输出出错,将dp[i][j]全部打印出来后,才知道是dp[1][1]出错了,因为dp[1][1]=max(dp[0][1],dp[0][0]+v[0]),需要用到dp[0][0],造成越界。所以,检验算法的正确性,可以先人工求解出dp[i][j]数组,再用程序将其打印出来,这样有利于我们快速找到问题所在。
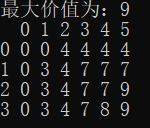
转换表(打印)
| 转换表(人工) | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 0 | 0 | 0 | 4 | 4 | 4 | 4 |
| 1 | 0 | 3 | 4 | 7 | 7 | 7 |
| 2 | 0 | 3 | 4 | 7 | 7 | 9 |
| 3 | 0 | 3 | 4 | 7 | 8 | 9 |
3、背包问题一定要先明确辅助数组的具体含义再确定转换方程,根据转换方程来确定初始化、遍历顺序和输出结果。
四、完整代码
#include#includeusing namespace std;const int max_weight = 5;const int n = 4;int main() {int i, j;int w[n] = { 2,1,4,3 }; //重量int v[n] = { 4,3,6,5 }; //价值int dp[n][max_weight+1];//辅助数组//初始化第0列(即背包容量为0)for (i = 0; i < n; i++)dp[i][0] = 0;//初始化第0行(即只有物品0)for (j = 1; j <= max_weight; j++) {if (w[0] <= j) dp[0][j] = v[0];elsedp[0][j] = 0;}//状态转移//先遍历物品再遍历背包for (i = 1; i < n; i++) { //遍历物品for (j = 1; j <= max_weight; j++) { //遍历背包if (j < w[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);}}//输出cout << dp[n - 1][max_weight] << endl;//回溯法求解装入物品i--; j--; //循环结束后,i=n,j=max_weight+1,故使用dp[n - 1][max_weight]须自减1cout << "最大价值时的背包物品为:" <=0) { if (dp[i][j] != dp[i - 1][j]) {cout << "物品" << i << endl;j -= w[i]; //装入物品i后背包的最大容量}i--; //物品i已经处理完成,接下来讨论物品i-1}return 0;}运行结果:

五、结语
当你想在你的代码中找到一个错误时,这很难;当你认为你的代码是不会有错误时,这就更难了。——Steve McConnell 《代码大全》
永远学习!永远进步!
码字不易,求个三连!
有问题也可以在评论区留言,有错误也欢迎各位大佬斧正,感激不尽!
关注我!后续会继续更新动态规划的问题分析,帮助你全面掌握!