点分治详解 ( 数据结构 )
啦啦啦,更新啦~
学习笔记:
前置知识:树的重心、线段树等类似数据结构。
点分治是一种十分高效的树上路径查询的数据结构,能在复杂度内查询所有路径信息。
它与线段树和分块的思想十分相似,用已求出的信息来帮助处理之后需要求的信息。
那么在树上呢,我们就可以先dfs一遍,然后用求出的dis信息来求解路径信息。
那么我们把所有的路径分为两种:经过当前根节点的和不经过当前根节点的。后者可以递归根节点转化为前者。
具体语境下求的东西不一样,这里介绍模板中距离小于k和等于k的做法。
算法流程:
1:首先选定最初的根节点。既然我们要对每个根节点递归地求解,并且每个根节点都要对所有子节点扫一遍,为了减少复杂度,我们尽量让每个根节点均摊总复杂度。那么这个节点就符合重心的定义了。(像极端情况下:链式图从中间开始和从两边开始复杂度差两倍)
2:在此根节点下计算题意相关路径信息。
3:递归实现1,2步骤。
这么说肯定有点抽象,我们结合两道例题来看看具体实战情况~
例题:
【模板】点分治1 - 洛谷
这题问的是典型的两点距离恰好为k的情况。
代码分为三个部分:
一:求重心
void get_root(int u,int fa,int total){siz[u]=1;maxp[u]=0;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;get_root(v,u,total);siz[u]+=siz[v];maxp[u]=max(siz[v],maxp[u]);}maxp[u]=max(maxp[u],total-siz[u]);if(!root||maxp[u]<maxp[root]){root=u;}}~
2:计算相关路径信息
本题我们求路径恰好为k的点对。那么我们每到一个根节点就求出所有点到根节点的距离dis,如果两个点的dis之和为k,即为解之一。但是其中包含所有点分治必须考虑的问题:就是去掉不符题意的部分答案。在这道题中,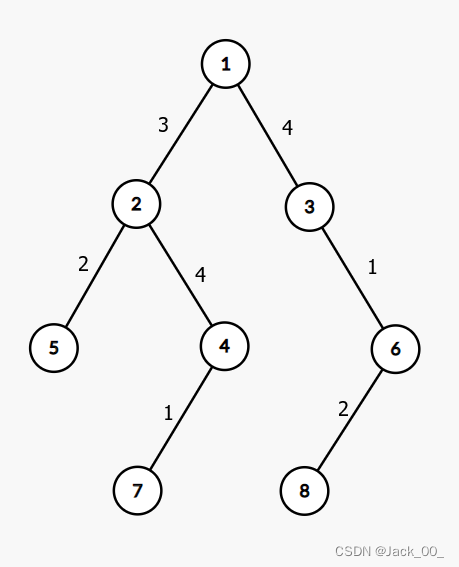
假如k==8,1节点为根节点,那么我们 2-1-3-6这条路径是符合的,但是1-2-4-7是不符合的,但是我们计算时都会把他们计算在内,不难发现不符合的都是路径上所有点都存在根节点的某一子树内。此时我们计算dis时用一个数组a存下每个点的编号,用距离dis排序,并用b数组存下每个节点存在于根节点的哪个子树。我们对a排序之后,用双指针扫一遍,看看是否存在路径恰为k且不在当前根节点的同一子树内。
bool cmp(int x,int y){return d[x]<d[y];}void get_dis(int u,int fa,int dis,int from){a[++tot]=u;d[u]=dis;b[u]=from;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;get_dis(v,u,dis+e[i].w,from);}}void calc(int u){//每一个根节点都要算一次当前的dis,并求出a,d,b数组;tot=0;a[++tot]=u;d[u]=0;b[u]=u;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(vis[v])continue;get_dis(v,u,e[i].w,v);}sort(a+1,a+tot+1,cmp);//排序后双指针扫一遍for(int i=1;i<=m;i++){int l=1,r=tot;if(ok[i])continue;while(lquery[i]) r--;//大了变小;else if(d[a[l]]+d[a[r]]<query[i]) l++;//小了变大;else if(b[a[l]]==b[a[r]]){//恰好相等但是位于同一子树;if(d[a[r]]==d[a[r-1]])r--;else l++;}else{//符合所有条件。ok[i]=true;break;}}}}3:递归1,2步骤求解。
每次找重心只会进行次(每棵子树大小不超过当前树大小一半),每次找到重心计算总计
复杂度,所以总计
复杂度,十分优秀。
void solve(int u){vis[u]=true;calc(u);for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(vis[v])continue;root=0;get_root(v,0,siz[v]);solve(root);}}总代码;
/*keep on going and never give up*/#includeusing namespace std;#define int long long#define MAX 0x3f3f3f3f#define fast std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);#define N 10001int n,m,query[101];int tot=0,head[N],maxp[N],siz[N],root,d[N],b[N],a[N];bool vis[N],ok[101];struct node{int to,nxt,w;}e[N<<1];void add(int a,int b,int c){e[++tot].nxt=head[a];e[tot].to=b;e[tot].w=c;head[a]=tot;}void get_root(int u,int fa,int total){siz[u]=1;maxp[u]=0;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;get_root(v,u,total);siz[u]+=siz[v];maxp[u]=max(siz[v],maxp[u]);}maxp[u]=max(maxp[u],total-siz[u]);if(!root||maxp[u]<maxp[root]){root=u;}}bool cmp(int x,int y){return d[x]<d[y];}void get_dis(int u,int fa,int dis,int from){a[++tot]=u;d[u]=dis;b[u]=from;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;get_dis(v,u,dis+e[i].w,from);}}void calc(int u){tot=0;a[++tot]=u;d[u]=0;b[u]=u;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(vis[v])continue;get_dis(v,u,e[i].w,v);}sort(a+1,a+tot+1,cmp);for(int i=1;i<=m;i++){int l=1,r=tot;if(ok[i])continue;while(lquery[i]) r--;else if(d[a[l]]+d[a[r]]>n>>m;for(int i=1;i>u>>v>>w;add(u,v,w);add(v,u,w);}for(int i=1;i>query[i];maxp[0]=n;get_root(1,0,n);solve(root);for(int i=1;i<=m;i++){if(ok[i])cout<<"AYE"<<endl;else cout<<"NAY"<<endl;}}Tree - 洛谷
求路径<=k的。
第二题与第一题大体相似,主要区别在第二部分的去除不符信息:
void get_dis(int u,int fa,int dis){a[++tot]=dis;d[u]=dis;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;get_dis(v,u,dis+e[i].w);}}int calc(int u,int w){tot=0;d[u]=w;get_dis(u,0,d[u]);sort(a+1,a+tot+1);int l=1,r=tot,res=0;while(l<r){if(a[l]+a[r]<=k){res+=r-l;l++;}else r--;}return res;}void solve(int u){vis[u]=1;ans+=calc(u,0);for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(vis[v])continue;ans-=calc(v,e[i].w);//容斥root=0;get_root(v,0,siz[v]);solve(root);}}我们容斥一下,用总的减去当前子树下各自子树下路径小于k的。这里我们对每个子树再calc一次,但是初始dis设为子树根节点到当前重心根节点距离,这样就能完美求出位于同一子树下的路径数量。这么搞搞就行了。
完整代码:
/*keep on going and never give up*/#includeusing namespace std;#define int long long#define MAX 0x3f3f3f3f#define fast std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);#define N 100010int n,m,query[101];int tot=0,head[N],maxp[N],siz[N],root,d[N],ans,a[N],k;bool vis[N],ok[101];struct node{int to,nxt,w;}e[N<<1];void add(int a,int b,int c){e[++tot].nxt=head[a];e[tot].to=b;e[tot].w=c;head[a]=tot;}void get_root(int u,int fa,int total){siz[u]=1;maxp[u]=0;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;get_root(v,u,total);siz[u]+=siz[v];maxp[u]=max(siz[v],maxp[u]);}maxp[u]=max(maxp[u],total-siz[u]);if(!root||maxp[u]<maxp[root]){root=u;}}void get_dis(int u,int fa,int dis){a[++tot]=dis;d[u]=dis;for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa||vis[v])continue;get_dis(v,u,dis+e[i].w);}}int calc(int u,int w){tot=0;d[u]=w;get_dis(u,0,d[u]);sort(a+1,a+tot+1);int l=1,r=tot,res=0;while(l<r){if(a[l]+a[r]<=k){res+=r-l;l++;}else r--;}return res;}void solve(int u){vis[u]=1;ans+=calc(u,0);for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(vis[v])continue;ans-=calc(v,e[i].w);root=0;get_root(v,0,siz[v]);solve(root);}}//路径>n;for(int i=1;i>u>>v>>w;add(u,v,w);add(v,u,w);}cin>>k;get_root(1,0,n);solve(root);cout<<ans;}

