算法笔记(四)——大整数运算(附带模板)
未来属于那些相信梦想,并愿意为之付诸行动的人![]() 。
。


![]()
![]()
大整数的存储
大整数的四则运算
高精度加法
高精度减法
高精度与低精度的乘法
高精度与低精度的除法
对一道A+B的题目,如果A和B的范围在int范围内,那么相信大家很快就能写出程序。但是如果A和B是有着1000个数位的整数,恐怕就没有办法用已有的数据类型来表示了。这时就只能老实的去模拟加减乘除的过程了.
大整数的存储
很简单,使用数组即可。例如定义int型数组d[1000],那么这个数组中的每一位就代表了存放的整数的每一位.如将整数12456存储到数组中,则有d[0]=6,d[1]=5,d[2]=4,d[3]=3,d[4]=2,d[5]=1;即整数的高位存储在数组的高位,整数的低位存储在数组的低位。不反过来存储的原因是,在进行运算的时候都是从整数的低位到高位进行枚举的,顺位存储和这种思维组合。但是也会由此产生一个需要注意的问题:把整数按字符串%s读入的时候,实际上是逆序存储,因此在读入之后需要在另存为致d[]数组的时候反转一下.
接下来主要介绍四个运算:1.高精度加法;2.高精度减法;3.高精度的乘法;4. 高精度的除法;
大整数的四则运算
高精度加法

加法步骤:将该位上的两个与进位相加,得到的结果取个位数作为该位结果,取十位数作为新的进位。
代码:
vector Add(vector& A,vector& B){ vector c; int t=0; for(int i=0;i<A.size()||i<B.size();i++) { if(i<A.size()) t+=A[i]; if(i<B.size()) t+=B[i]; c.push_back(t%10);//取个位作为结果 t/=10;//取十位进行进位 } if(t) c.push_back(1); return c;}上面大概十行代码,非常简介,因此不需要对高精度有所畏惧,只要懂的原理并写过一次基本上就可以记住.
下面我以例题演示完整代码 :
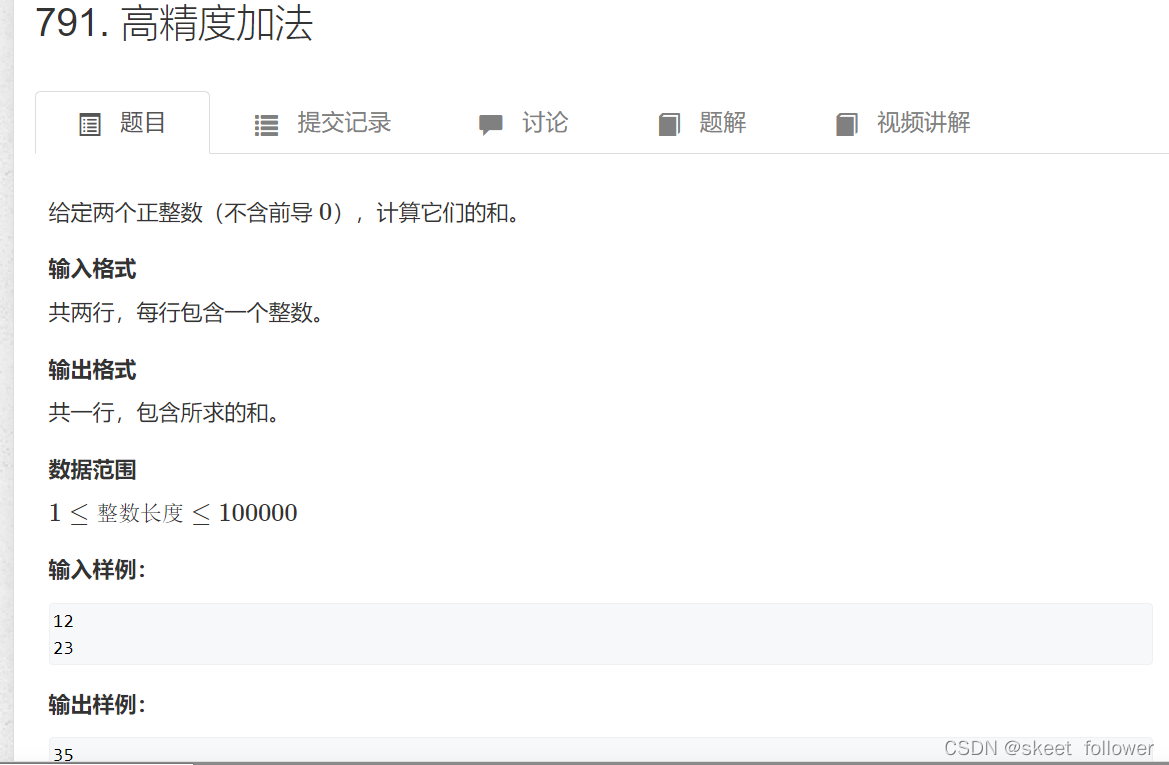
#include#includeusing namespace std;vector Add(vector& A,vector& B){ vector c; int t=0; for(int i=0;i<A.size()||i<B.size();i++) { if(i<A.size()) t+=A[i]; if(i<B.size()) t+=B[i]; c.push_back(t%10); t/=10; } if(t) c.push_back(1); return c;}int main(){ string a,b;//位数过大,用字符串形式输入 vectorA,B; cin>>a>>b;//123+89 for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0');//将其转化成整型,从低位到高位依次存储到vector中 for(int i=b.size()-1;i>=0;i--)B.push_back(b[i]-'0'); auto c=Add(A,B);//A+B相加 for(int i=c.size()-1;i>=0;i--)//因为是低位开始相加的,输出应该逆序 { printf("%d",c[i]); } return 0;}上面针对的两个对象都是非负整数。如果有一方是负的,可以在转换到数组这一步时去掉符号,然后采用高精度减法;如果两个都是负的,就去掉负号后用高精度加法,最后再把负号加回去即可.
高精度减法

减法步骤:对某一步,比较被减位和减位,如果不够减,则令被减位的高位减1,被减位加10再进行减法;如果够减,则直接减.最后一步要注意减法后高位可能有多余的0,要去除他们,但也要保证结果至少有一位数.
vector sub(vector& A,vector& B){ vector c; for(int i=0,t=0;i<A.size();i++) { t=A[i]-t; if(i=0和t<0两种情况 if(t1&&c.back()==0) c.pop_back(); return c;}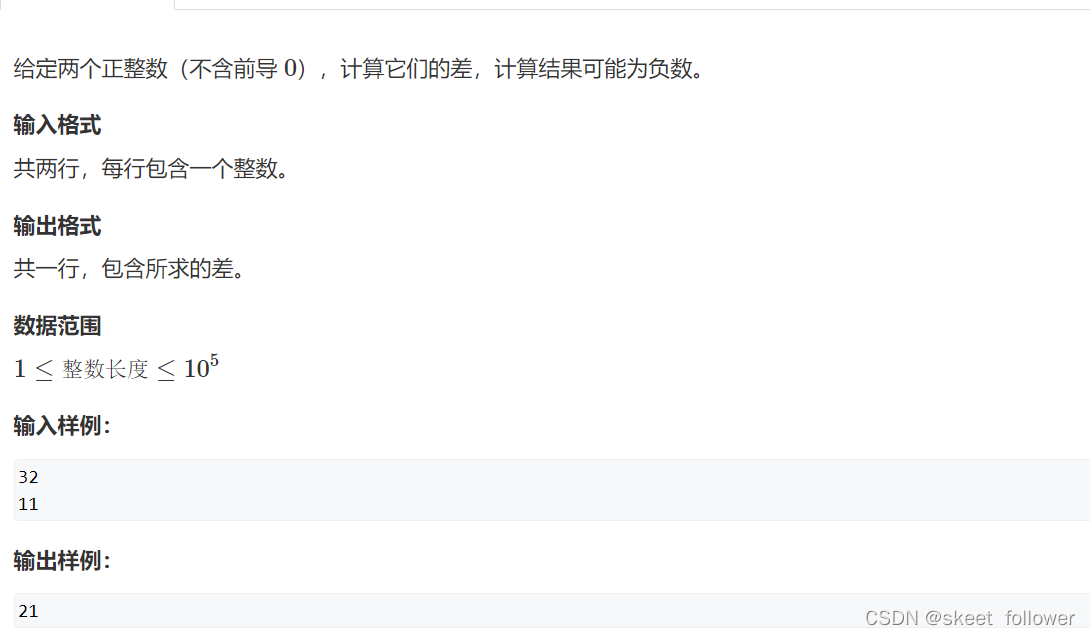
#include#includeusing namespace std;bool cmp(vector& A,vector& B){ if(A.size()!=B.size()) return A.size()>B.size(); for(int i=A.size()-1;i>=0;i--) { if(A[i]!=B[i]) { return A[i]>B[i]; } } return true;}vector sub(vector& A,vector& B){ vector c; for(int i=0,t=0;i<A.size();i++) { t=A[i]-t; if(i<B.size()) t-=B[i]; c.push_back((t+10)%10); if(t1&&c.back()==0) c.pop_back(); return c;}int main(){ //145-67 string a,b; vector A,B; cin>>a>>b; for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0'); for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0'); if(cmp(A,B)) { auto c=sub(A,B); for(int i=c.size()-1;i>=0;i--) { printf("%d",c[i]); } } else{ auto c=sub(B,A); printf("-"); for(int i=c.size()-1;i>=0;i--) { printf("%d",c[i]); } } return 0;}高精度与低精度的乘法
所谓的低精度就是可以用基本数据类型存储的数据,例如int型.这里描述的就是bign类型与Int类型的乘法,其做法和小学学的有点不一样.以147*35为例,这里把147视为高精度与bign类型,而35视为int类型,并且在下面的过程中,始终将35作为一个整体看待.
 步骤:取bign的某位与int型整体相乘,再与进位相加,所得结果的各位是作为该位结果,高位部分作为新的进位。
步骤:取bign的某位与int型整体相乘,再与进位相加,所得结果的各位是作为该位结果,高位部分作为新的进位。
vector mul(vector& A,int b){ vector c; int t=0; for(int i=0;i<A.size()||t;i++) { if(i 1 && c.back() == 0) c.pop_back(); return c;}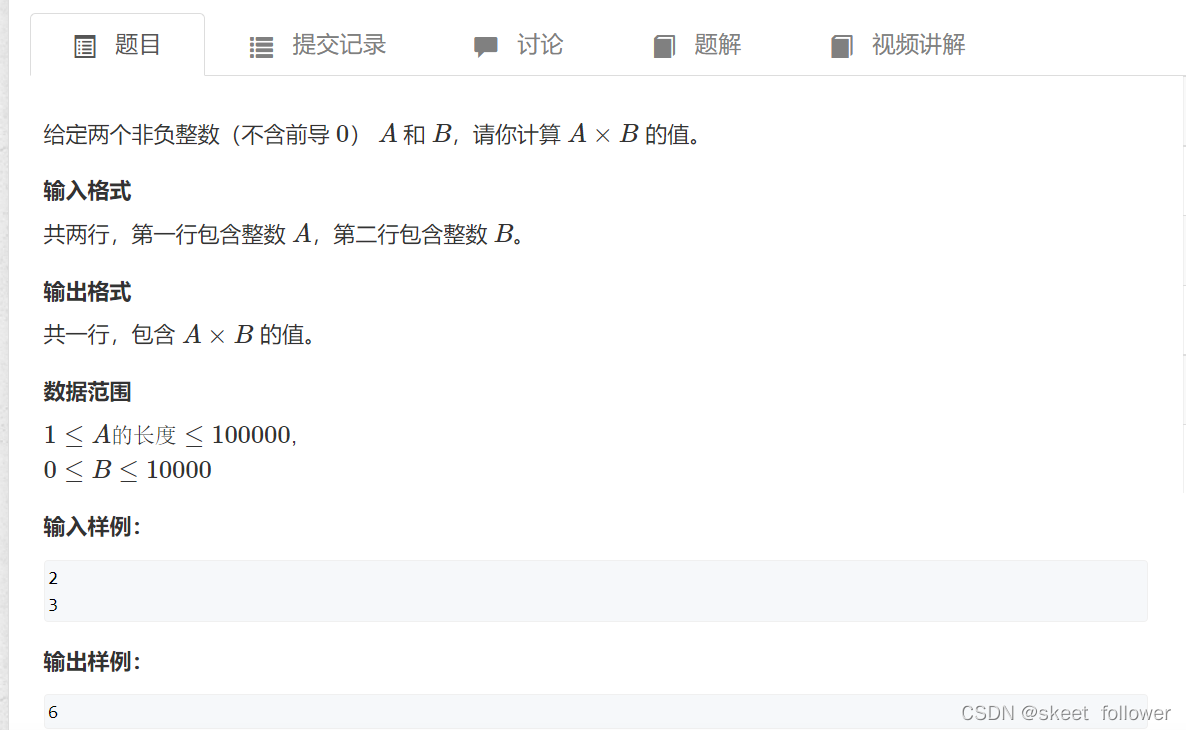 代码:
代码:
#include#includeusing namespace std;vector mul(vector& A,int b){ vector c; int t=0; for(int i=0;i<A.size()||t;i++) { if(i 1 && c.back() == 0) c.pop_back(); return c;}int main(){ string a; int b; cin>>a>>b; vector A; for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0'); auto c=mul(A,b); for(int i=c.size()-1;i>=0;i--)printf("%d",c[i]); return 0;}高精度与低精度的除法

步骤:上一步的余数除以10加上该步的位,得到该步临时的被除数,将其与除数比较:如果不够除,则该位的商为0;如果够除,则商即为对应的商,余数即为对应的余数。最后一步要注意减法后高位可能有多余的0,要去除他们呢,但也要保证结果至少有一位数
vector div(vector &A, int b, int &r){ vector C; r = 0; for (int i = A.size() - 1; i >= 0; i -- ) { r = r * 10 + A[i]; C.push_back(r / b); r %= b; } reverse(C.begin(), C.end()); while (C.size() > 1 && C.back() == 0) C.pop_back(); return C;}
代码:
#include#includeusing namespace std;vector div(vector &A, int b, int &r){ vector C; r = 0; for (int i = A.size() - 1; i >= 0; i -- ) { r = r * 10 + A[i]; C.push_back(r / b); r %= b; } reverse(C.begin(), C.end()); while (C.size() > 1 && C.back() == 0) C.pop_back(); return C;}int main(){ string a; int b; cin>>a>>b; vector A; for(int i=a.size()-1;i>=0;i--)A.push_back(a[i]-'0'); int r; auto c=div(A,b,r); for(int i=c.size()-1;i>=0;i--)printf("%d",c[i]); cout<<endl<<r<<endl; return 0;}


