一维数组中的前缀和

区域和检索——数组不可变

二维矩阵中的前缀和

二维区域和检索——矩阵不可变

一维数组中的前缀和

先看一道例题,力扣第303题。

区域和检索——数组不可变

没学过前缀和之前我们都会这样写。

class NumArray {private:    vector nums;public:    NumArray(vector& nums) { this->nums=nums;    } int sumRange(int left, int right) { int res=0; for(int i=left;i<=right;i++) {     res+=nums[i]; } return res;    }   };

这样写没问题,但是效率很低,sumRange会被频繁的调用，时间复杂度为O(n)。

而这道题如果利用前缀和来解题,时间复杂度就会降到O(1).

简单先介绍下前缀和:核心思想就是，创建一个新数组sum出来,用sum[i]记录num[0,1,,,,i-1]的和。

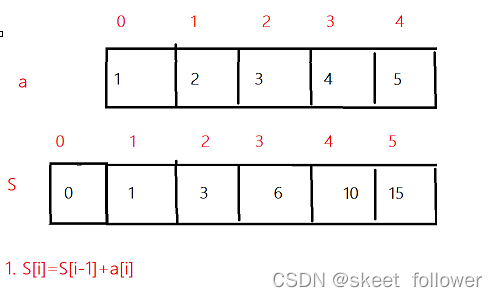
 如果我们想求索引区间[1,3]内所有元素的和,S[4]-s[1]就可以得出来,这样只需要做一次减法就可以得出来结果避免了多次for循环的调用，时间复杂度为O(1).

优化后的代码:

class NumArray {public:    vector sum;    NumArray(vector& nums) { int n=nums.size(); sum.resize(n+1);      // 计算sum的累加和 for(int i=0;i<n;i++) {     sum[i+1]=sum[i]+nums[i]; }    }     /* 查询闭区间 [left, right] 的累加和 */    int sumRange(int left, int right) {      return sum[right+1]-sum[left];    }};

趁热打铁再试一题:

#includeusing namespace std;const int N=100010;int n,m;int a[N],sum[N];int main(){    scanf("%d%d",&n,&m);    for(int i=0;i<n;i++) scanf("%d",&a[i]);    for(int i=0;i<n;i++) sum[i+1]=sum[i]+a[i];    while(m--)    { int l,r; scanf("%d%d",&l,&r); printf("%d\n",sum[r]-sum[l-1]);    }    return 0;}

前面我有一篇关于蓝桥杯的博客,里面的K倍区间就是对前缀和的应用，不过那道题对前缀和做了优化,想深入了解的可以看下:蓝桥杯——2017第八届C/C++真题[省赛][B组]_skeet follower的博客-CSDN博客

二维矩阵中的前缀和

首先介绍下二维矩阵的前缀和，这篇文章写的很好前缀和，这里我就拿大佬的思路来供我们参考学习.

步骤一：求 preSum
我们先从如何求出二维空间的 preSum[i][j]。

我们定义 preSum[i][j]preSum[i][j] 表示 从 [0,0][0,0] 位置到 [i,j][i,j] 位置的子矩形所有元素之和。
可以用下图帮助理解：

S(O, D) = S(O, C) + S(O, B) - S(O, A) + D

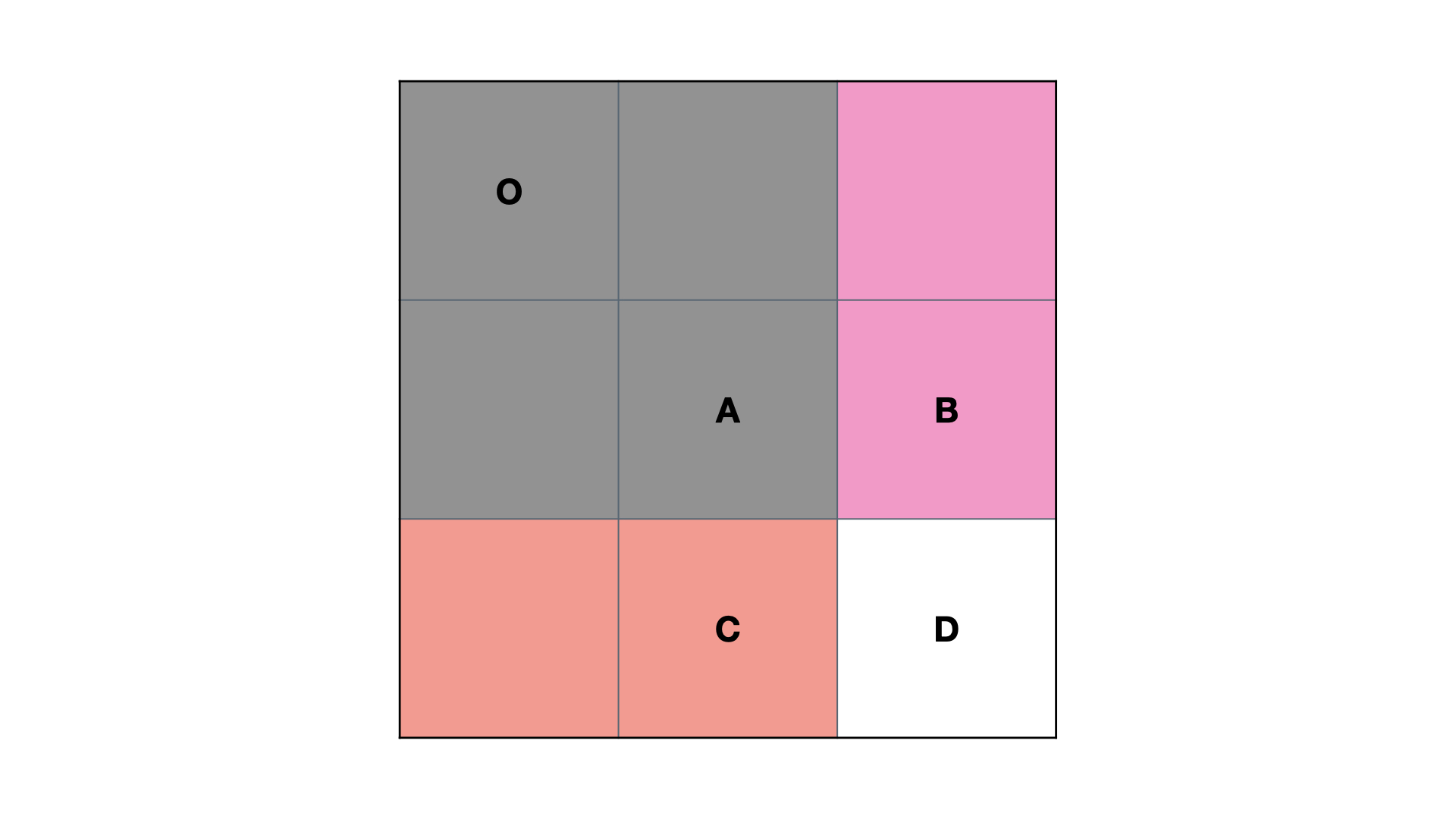
减去 S(O, A)S(O,A) 的原因是 S(O, C)S(O,C) 和 S(O, B)S(O,B) 中都有 S(O, A)S(O,A)，即加了两次 S(O, A)S(O,A)，所以需要减去一次 S(O, A)S(O,A)。

如果求 preSum[i][j]preSum[i][j] 表示的话，对应了以下的递推公式：

preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i][j]
步骤二：根据 preSum 求子矩形面积

前面已经求出了数组中从 [0,0][0,0] 位置到 [i,j][i,j] 位置的 preSum。下面要利用 preSum[i][j]preSum[i][j] 来快速求出任意子矩形的面积。

同样利用一张图来说明：

S(A, D) = S(O, D) - S(O, E) - S(O, F) + S(O, G)

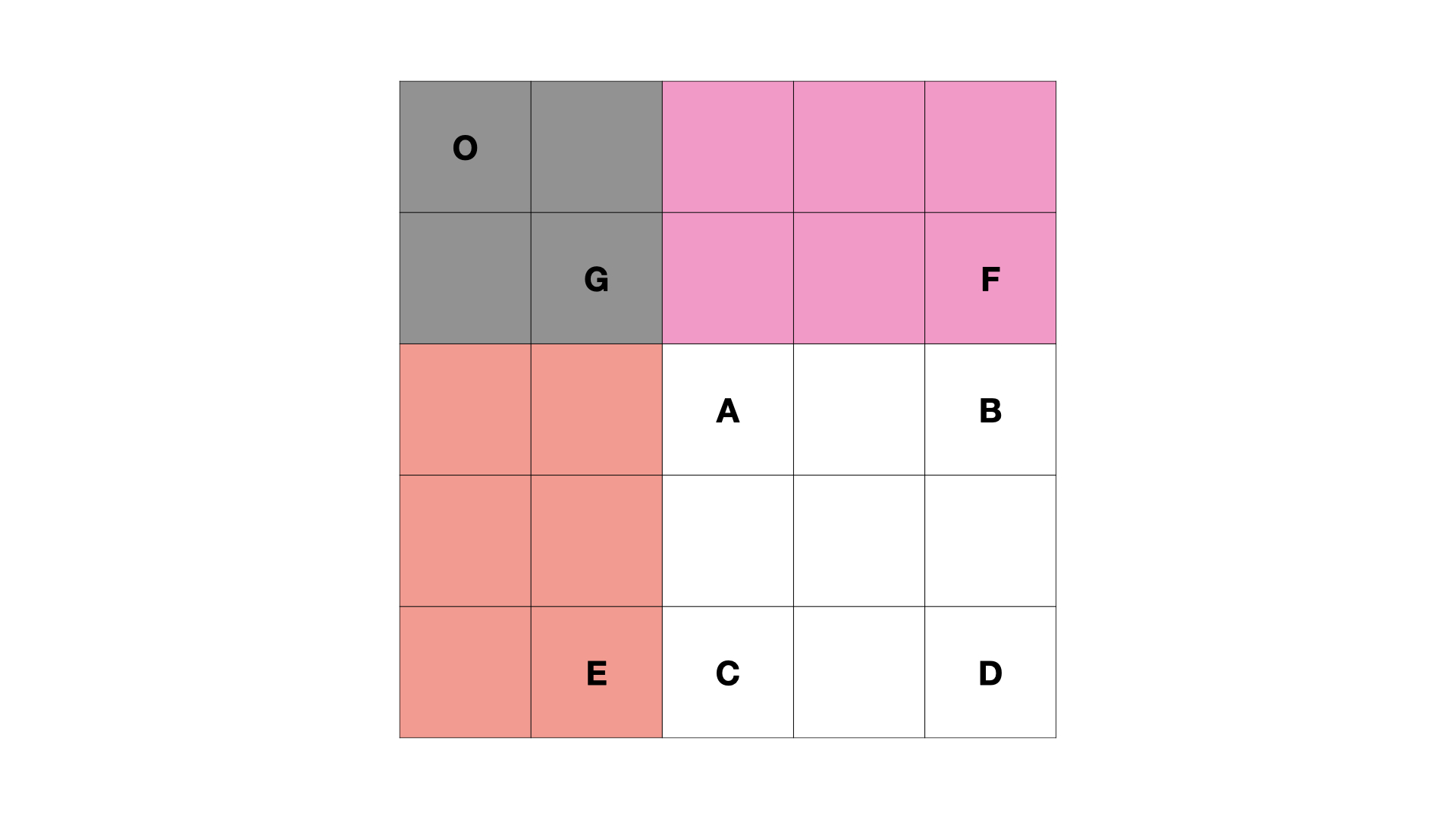
加上子矩形 S(O, G)S(O,G) 面积的原因是 S(O, E)S(O,E) 和 S(O, F)S(O,F) 中都有 S(O, G)S(O,G)，即减了两次 S(O, G)S(O,G)，所以需要加上一次 S(O, G)S(O,G)。

如果要求 [row1, col1][row1,col1] 到 [row2, col2][row2,col2] 的子矩形的面积的话，用 preSum 对应了以下的递推公式：

preSum[row2][col2] - preSum[row2][col1 - 1] - preSum[row1 - 1][col2] + preSum[row1 - 1][col1 - 1]

二维区域和检索——矩阵不可变

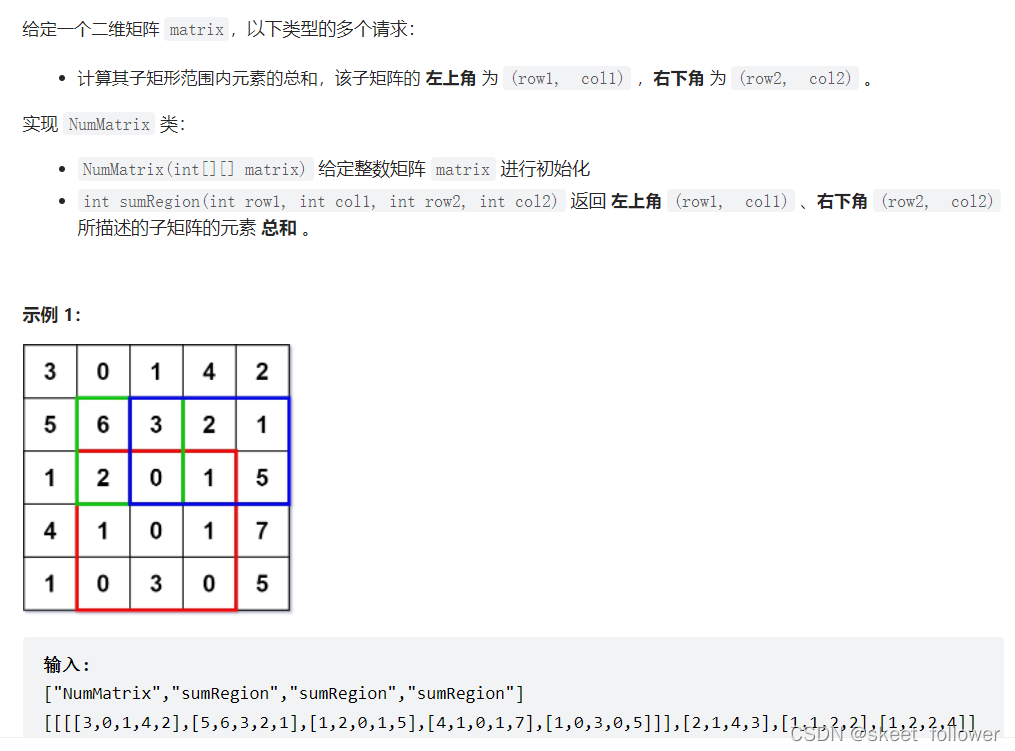
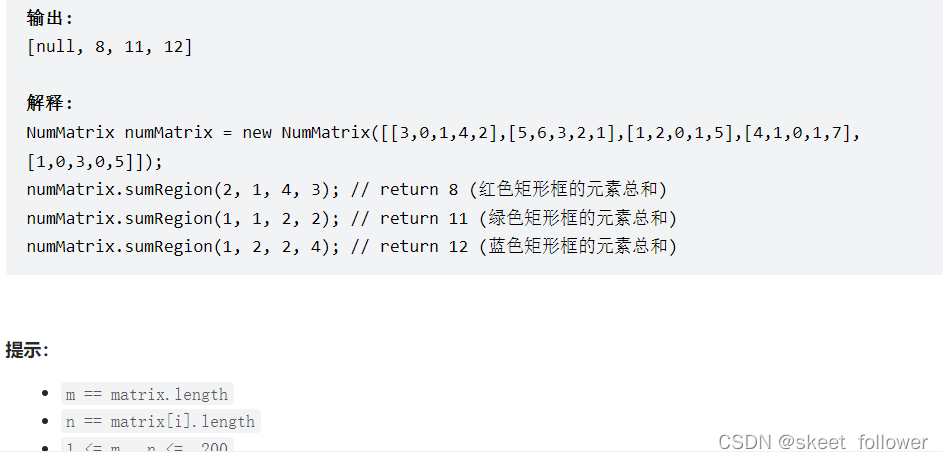
 代码

class NumMatrix {public:    vector<vector> sums;    NumMatrix(vector<vector>& matrix) { int m = matrix.size(); if (m > 0) {     int n = matrix[0].size();     sums.resize(m + 1, vector(n + 1));     for (int i = 0; i < m; i++) {  for (int j = 0; j < n; j++) {      sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];  }     } }    }    int sumRegion(int row1, int col1, int row2, int col2) { return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];    }};

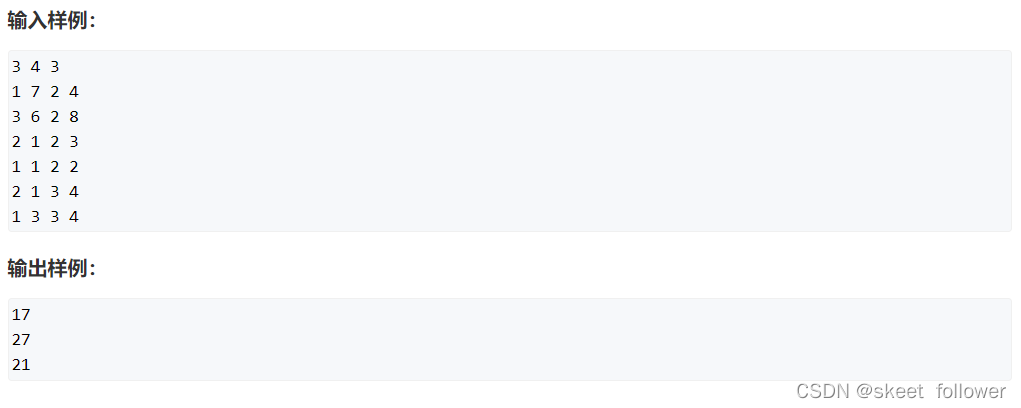 代码

#includeusing namespace std;const int N=1010;int n,m,q;int a[N][N],s[N][N];int main(){    scanf("%d%d%d",&n,&m,&q);    for(int i=1;i<=n;i++)    { for(int j=1;j<=m;j++) {     scanf("%d",&a[i][j]); }    }    for(int i=1;i<=n;i++)    { for(int j=1;j<=m;j++) {     s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]; }    }    while(q--)    { int x1,y1,x2,y2; scanf("%d%d%d%d",&x1,&y1,&x2,&y2); printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);     }    return 0;}

历史新知