数据结构-栈和队列
栈和队列
- 栈和队列的定义和特点
-
- 栈——后进先出
-
- 栈的相关概念
- 栈与一般线性表的区别
- 栈的表示与实现
-
- 栈的抽象数据类型的类型定义
- 队列 ——先进先出
- 相关案例
-
- 进制转换
- 括号匹配的检验
- 表达式求值
栈和队列的定义和特点
- 栈和队列是限定插入和删除只能在表的“端点”进行的线性表
栈——后进先出

定义:栈(stack)是一个特殊的线性表,是限定仅在一端(通常是表尾)进行插入和删除操作的线性表。
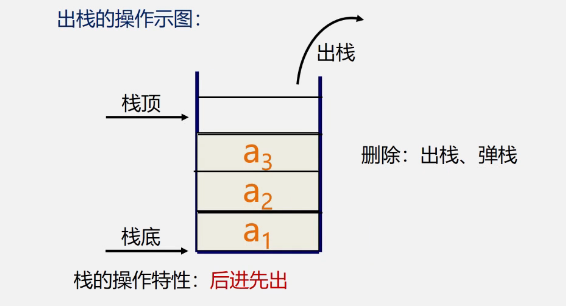
又称为后进先出(Last In First Out)的线性表,简称LIFO结构。
栈的相关概念
-
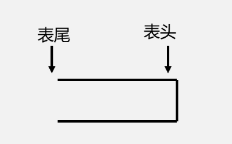
栈是仅在表尾进行插入、删除操作的线性表。
表尾(即an端)称为栈顶Top;表头(即a端)称为栈底Base

-
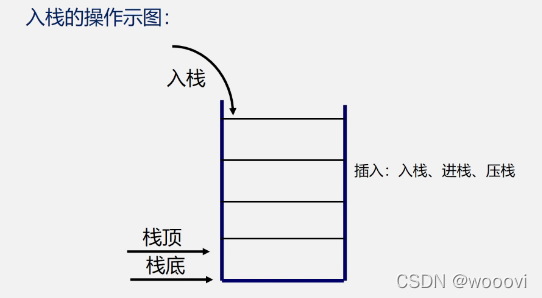
插入元素到栈顶(即表尾)的操作,称为入栈(push)。
-
从栈顶(即表尾)删除最后一个元素的操作,称为出栈(pop)。
栈与一般线性表的区别

栈的表示与实现
栈的抽象数据类型的类型定义

- lnitStack(&S) 初始化操作
操作结果:构造一个空栈S。 - DestroyStack(&S)销毁栈
操作初始条件:栈S已存在。
操作结果:栈S被销毁。 - StackEmpty(S) 判定S是否为空栈
初始条件:栈S已存在。
操作结果:若栈S为空栈,则返回TRUE,
否则FALSE。 - StackLength(S) 求栈的长度
初始条件:栈s存在。
操作结果:返回的元素个数,即栈的长度。 - GetTop(S. &e) 取栈顶元素
初始条件:栈S已存在且非空。
操作结果:用e返回S的栈顶元素。 - ClearStack(&S) 栈置空操作
初始条件:栈S已存在。
操作结果:将S清为空栈。 - Push(&S, e) 入栈操作
初始条件:栈S已存在。
操作结果:插入元素e 为新的栈顶元素。 - Pop(&s,&e) 出栈操作
初始条件:栈S已存在且非空。
操作结果:删除S的栈顶元素an,并用e返回其值。
队列 ——先进先出
解决排队问题
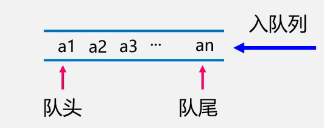
队列(queue)是一种先进先出(Frist In Frist Out ----FIFO)的线性表。在表—端插入(表尾),在另一端(表头)删除
相关案例
进制转换
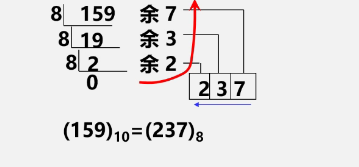
十进制整数N向其它进制数d(二、八、十六)的转换是计算机实现的基本问题
转换法则︰除以d倒取余
该转换法则对应于一个简单算法原理:
n=(n div d) * d + n mod d其中: div为整除运算,mod为求余运算
- 例 把十进制数159转成为八进制数
-
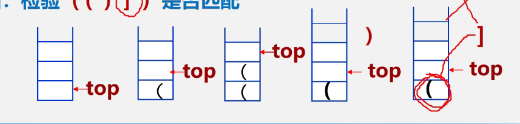
括号匹配的检验
- 假设表达式中允许包含两种括号:圆括号和方括号
- 其嵌套的顺序随意,即:
1.([] ())或〔( [][ ] )]为正确格式;
2.[ (])为错误格式;
3.( [ ())或(()])为错误格式。
例如:检验(()])是否匹配
表达式求值
- 表达式求值是程序设计语言编译中一个最基本的问题,它的实现也需要运用栈。
- 这里介绍的算法是由运算符优先级确定运算顺序的对表达式求值算法
——算符优先算法。 - 表达式的组成
- 操作数(operand):常数、变量。
- 运算符(operator):算术运算符、关系运算符和逻辑运算符。
- 界限符(delimiter):左右括弧和表达式结束符。
- 任何一个算术表达式都由操作数(常数、变量)、算术运算符(+、-、*、/)和界限符(括号、表达式结束符‘#’、虚设的表达式起始符‘#’)组成。后两者统称为算符。
- 例如: #3 * ( 7 - 2 ) #



