【蓝桥杯】一学就会的小技巧（五）：矩阵快速幂

🍎前言：

• 一学就会的小技巧（一）：前缀和
• 一学就会的小技巧（二）：差分
• 一学就会的小技巧（三）：快速幂
• 一学就会的小技巧（四）：龟速乘
• 一学就会的小技巧（六）：矩阵快速幂的应用
• 数论基础—素数筛、最大公约数、最小公倍数
• 省赛真题—K倍区间（前缀和，数学，思维）

🏅🏅前面已经介绍了快速幂这个技巧，快速幂除了可以拓展出龟速乘外，还可以用于计算矩阵的幂。矩阵快速幂在学会了快速幂的情况下很好掌握，只需要在矩阵乘法的基础上套一个快速幂模板就可以了。

题目传送门🚀🚀🚀

🍬矩阵快速幂：

👩🏻‍🏫如果你忘记了矩阵乘法，可以先来回顾一下~

• 对于矩阵matrixA[n][p]与matrixB[p][m]，$matrixA\times matrixB$可以得到一个新的矩阵matrixC[n][m]。

• 矩阵的乘法不满足交换律，即$matrixA\times matrixB$不等于$matrixB\times matrixA$。

• 两个矩阵可以相乘的条件是：前一个矩阵的列数与后一个矩阵的行数相等。

• 矩阵乘法的规则：

  

  简言之就是前行乘后列。

🍦矩阵乘法代码模板（Java）：

public static long[][] matrixMultiply(long[][] matrixA, long[][] matrixB) {int n = matrixA.length, p = matrixB.length, m = matrixB[0].length;if (p != matrixA[0].length)return null;long[][] res = new long[n][m];for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)for (int k = 0; k < p; k++)res[i][j] += matrixA[i][k] * matrixB[k][j];return res;}

👩🏻‍🏫题目要我们求矩阵的n次幂，只需要将快速幂模板里的普通乘法改为矩阵乘法，结果是一个n阶方阵$matrixC[n][n]$。

⭐需要注意的是矩阵快速幂中的结果初始值要设置为单位矩阵。

👉🏻什么是单位矩阵？

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。

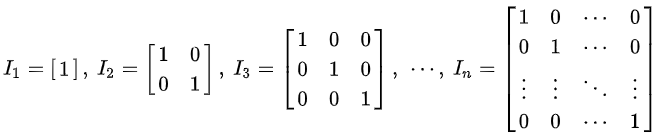
🍦AC代码（C语言）：

#includeusing namespace std;typedef long long ll;const ll m = 1e9 + 7;ll n;ll p;ll matrix[105][105];ll res[105][105] = {0};void mult1() {    ll temp[105][105] = {0};    for (int i = 0; i < n; i++) for (int j = 0; j < n; j++)     for (int k = 0; k < n; k++)  temp[i][j] = (temp[i][j] + matrix[i][k] * matrix[k][j]) % m;    for (int i = 0; i < n; i++) for (int j = 0; j < n; j++)     matrix[i][j] = temp[i][j];}void mult2() {    ll temp[105][105] = {0};    for (int i = 0; i < n; i++) for (int j = 0; j < n; j++)     for (int k = 0; k < n; k++)  temp[i][j] = (temp[i][j] + res[i][k] * matrix[k][j]) % m;    for (int i = 0; i < n; i++) for (int j = 0; j < n; j++)     res[i][j] = temp[i][j];}int main() {    scanf("%lld %lld", &n, &p);    for (int i = 0; i < n; i++) for (int j = 0; j < n; j++)     scanf("%lld", &matrix[i][j]);    for (int i = 0; i < n; i++) res[i][i] = 1;    while (p > 0) { if (p & 1 == 1)     mult2(); mult1(); p = p >> 1;    }    for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) {  printf("%lld ", res[i][j] % m); } printf("\n");    }    return 0;}

• temp[i][j] = (temp[i][j] + res[i][k] * matrix[k][j]) % m这条语句写成temp[i][j] += res[i][k] * matrix[k][j] % m提交到洛谷的OJ上过不了任何样例，算是个小坑吧，排查了好久~

• 试着用Java写了一下，提交上去直接RE了，本地调试没有任何问题，和C语言的输出结果都是一样的（无语）🙃

🍦Java模板代码：

import java.util.Scanner;public class Main {    public static final long mod = 1000000007;    public static long[][] matrixMultiply(long[][] matrixA, long[][] matrixB) { int n = matrixA.length, p = matrixB.length, m = matrixB[0].length; if (p != matrixA[0].length)     return null; long[][] ans = new long[n][m]; for (int i = 0; i < n; i++)     for (int j = 0; j < m; j++) {  for (int k = 0; k < p; k++)      ans[i][j] += (matrixA[i][k] % mod) * (matrixB[k][j] % mod) % mod;ans[i][j] = ans[i][j] % mod;     } return ans;    }    public static long[][] fastMatrixPow(long[][] matrix, long k) { int len = matrix.length; long[][] res = new long[len][len]; for (int i = 0; i < len; i++)     res[i][i] = 1; while (k > 0) {     if ((k & 1) == 1)  res = matrixMultiply(res, matrix);     matrix = matrixMultiply(matrix, matrix);     k = k >> 1; } return res;    }    public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); long k = sc.nextInt(); long[][] matrix = new long[n][n]; for (int i = 0; i < n; i++)     for (int j = 0; j < n; j++)  matrix[i][j] = sc.nextInt(); sc.close(); long[][] res = fastMatrixPow(matrix, k); for (int i = 0; i < n; i++) {     if (i != 0)  System.out.println("");     for (int j = 0; j < n; j++)  System.out.print(res[i][j] % mod + " "); }    }}

🍌🍌🍌
本文介绍了第五个小技巧——矩阵快速幂，洛谷的OJ上提交我的Java版代码直接Runtime Error，C语言倒是可以过，但是赋值语句a = a+b写成a+=b过不了样例，如果你知道为什么，欢迎在评论区留言~
🍍🍍🍍
创作不易，如果觉得本文对你有所帮助的话请动动小手，给博主点个免费的赞吧。🙇🏻‍♀️
🍉🍉🍉
@作者：Mymel_晗，计科专业大学牲一枚，请大佬们多多关照~

天天排行榜