统计学习导论(ISLR)第五章课后习题
统计学习导论(ISLR)
参考资料:
The Elements of Statistical Learning
An Introduction to Statistical Learning
统计学习导论(ISLR)(二):统计学习概述
统计学习导论(ISLR)(三):线性回归
统计学习导论(ISLR)(四):分类
统计学习导论(ISLR)(五):重采样方法(交叉验证和boostrap)
ISLR统计学习导论之R语言应用(二):R语言基础
ISLR统计学习导论之R语言应用(三):线性回归R语言代码实战
ISLR统计学习导论之R语言应用(四):分类算法R语言代码实战
ISLR统计学习导论之R语言应用(五):R语言实现交叉验证和bootstrap
统计学习导论(ISLR) 第三章课后习题
统计学习导论(ISLR) 第四章课后习题
统计学习导论(ISLR)第五章课后习题
文章目录
- 统计学习导论(ISLR)
- 第五章课后代码习题
- 5.
-
- a
- b.
- c
- d
- 6.
-
- a
- b
- c
- d
- 7.
-
- a
- b
- c
- d
- 8.
-
- a
- b
- c
- d
- e
- f
- 9.
-
- a
- b
- c
- d
- e
- f
- g
- h
第五章课后代码习题
5.
在第4章中,我们使用logistic回归在违约数据集上预测用户是否违约。我们将使用验证集方法估计该逻辑回归模型的测试误差。
a
拟合logistic回归模型
#导入相关库library(ISLR2)set.seed(7)glm.fit <- glm(default~income + balance, data=Default,family = binomial)summary(glm.fit)
Call:glm(formula = default ~ income + balance, family = binomial, data = Default)Deviance Residuals: Min1Q Median3Q Max -2.4725 -0.1444 -0.0574 -0.0211 3.7245 Coefficients:Estimate Std. Error z value Pr(>|z|) (Intercept) -1.154e+01 4.348e-01 -26.545 < 2e-16 *income2.081e-05 4.985e-06 4.174 2.99e-05 *balance 5.647e-03 2.274e-04 24.836 < 2e-16 *---Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1(Dispersion parameter for binomial family taken to be 1) Null deviance: 2920.6 on 9999 degrees of freedomResidual deviance: 1579.0 on 9997 degrees of freedomAIC: 1585Number of Fisher Scoring iterations: 8b.
使用验证集方法,估计该模型的测试误差。
# 1.划分训练集和验证集set.seed(7)train = sample(10000, 5000)# 2.在训练集上面拟合模型glm.fit = glm(default ~ income + balance, data = Default, family = binomial, subset = train)# 3.预测验证集上的结果glm.pred = rep("No", dim(Default)[1]/2)glm.probs = predict(glm.fit, Default[-train, ], type = "response")glm.pred[glm.probs > 0.5] = "Yes"# 4.计算测试误差mean(glm.pred != Default[-train, ]$default)0.0242
c
使用不同的训练集拟合三次模型比较测试误差
# 1.划分训练集和验证集train = sample(10000, 5000)# 2.在训练集上面拟合模型glm.fit = glm(default ~ income + balance, data = Default, family = binomial, subset = train)# 3.预测验证集上的结果glm.pred = rep("No", dim(Default)[1]/2)glm.probs = predict(glm.fit, Default[-train, ], type = "response")glm.pred[glm.probs > 0.5] = "Yes"# 4.计算测试误差mean(glm.pred != Default[-train, ]$default)0.027
# 1.划分训练集和验证集train = sample(10000, 5000)# 2.在训练集上面拟合模型glm.fit = glm(default ~ income + balance, data = Default, family = binomial, subset = train)# 3.预测验证集上的结果glm.pred = rep("No", dim(Default)[1]/2)glm.probs = predict(glm.fit, Default[-train, ], type = "response")glm.pred[glm.probs > 0.5] = "Yes"# 4.计算测试误差mean(glm.pred != Default[-train, ]$default)0.0272
# 1.划分训练集和验证集train = sample(10000, 5000)# 2.在训练集上面拟合模型glm.fit = glm(default ~ income + balance, data = Default, family = binomial, subset = train)# 3.预测验证集上的结果glm.pred = rep("No", dim(Default)[1]/2)glm.probs = predict(glm.fit, Default[-train, ], type = "response")glm.pred[glm.probs > 0.5] = "Yes"# 4.计算测试误差mean(glm.pred != Default[-train, ]$default)0.0274
结果显示测试误差分别为2.7%,2.72%,2.74%
d
引进student到模型中,使用验证集方法检验模型是否有提升
# 1.划分训练集和验证集set.seed(7)train = sample(10000, 5000)# 2.在训练集上面拟合模型glm.fit = glm(default ~ income + balance + student, data = Default, family = binomial, subset = train)# 3.预测验证集上的结果glm.pred = rep("No", dim(Default)[1]/2)glm.probs = predict(glm.fit, Default[-train, ], type = "response")glm.pred[glm.probs > 0.5] = "Yes"# 4.计算测试误差mean(glm.pred != Default[-train, ]$default)0.0242
从结果来看基本没有提升模型的准确性
6.
下面我们使用bootstrp来估计logistic回归系数的标准差,和glm()和summary()得出的结果进行比较。
同样适用违约数据集
a
拟合logistics回归模型并且用summar()函数得到回归洗漱
set.seed(7)glm.fit = glm(default ~ income + balance, data = Default, family = binomial)summary(glm.fit)
Call:glm(formula = default ~ income + balance, family = binomial, data = Default)Deviance Residuals: Min1Q Median3Q Max -2.4725 -0.1444 -0.0574 -0.0211 3.7245 Coefficients:Estimate Std. Error z value Pr(>|z|) (Intercept) -1.154e+01 4.348e-01 -26.545 < 2e-16 *income2.081e-05 4.985e-06 4.174 2.99e-05 *balance 5.647e-03 2.274e-04 24.836 < 2e-16 *---Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1(Dispersion parameter for binomial family taken to be 1) Null deviance: 2920.6 on 9999 degrees of freedomResidual deviance: 1579.0 on 9997 degrees of freedomAIC: 1585Number of Fisher Scoring iterations: 8b
编写函数boot.fn,得到回归系数
boot.fn = function(data, index) { coef(glm(default ~ income + balance, data = data, family = binomial, subset = index))}c
使用boot()函数计算bootstrap的回归系数估计值
library(boot)boot(Default, boot.fn, 100)Warning message:"package 'boot' was built under R version 4.0.5"ORDINARY NONPARAMETRIC BOOTSTRAP
Call:boot(data = Default, statistic = boot.fn, R = 100)
Bootstrap Statistics : original bias std. errort1* -1.154047e+01 3.279628e-03 4.032749e-01t2* 2.080898e-05 4.685383e-07 4.589626e-06t3* 5.647103e-03 -1.132436e-05 2.206669e-04d
可以看出两者结果相差不大。
7.
在R语言代码实战中我们介绍了使用cv.glm()函数计算LOOCV的测试错误率。
同样的,我们也可以只适用glm()和predic()加上for循环来实现这些结果。我们使用weekly数据集分析
a
首先拟合logistic回归模型
set.seed(7)glm.fit = glm(Direction ~ Lag1 + Lag2, data = Weekly, family = binomial)summary(glm.fit)
Call:glm(formula = Direction ~ Lag1 + Lag2, family = binomial, data = Weekly)Deviance Residuals: Min 1Q Median 3Q Max -1.623 -1.261 1.001 1.083 1.506 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 0.22122 0.06147 3.599 0.000319 *Lag1 -0.03872 0.02622 -1.477 0.139672 Lag2 0.06025 0.02655 2.270 0.023232 * ---Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1(Dispersion parameter for binomial family taken to be 1) Null deviance: 1496.2 on 1088 degrees of freedomResidual deviance: 1488.2 on 1086 degrees of freedomAIC: 1494.2Number of Fisher Scoring iterations: 4b
去除第一个观测值以外所有的数据作为训练集拟合模型
glm.fit = glm(Direction ~ Lag1 + Lag2, data = Weekly[-1, ], family = binomial)summary(glm.fit)
Call:glm(formula = Direction ~ Lag1 + Lag2, family = binomial, data = Weekly[-1, ])Deviance Residuals: Min1Q Median3Q Max -1.6258 -1.2617 0.9999 1.0819 1.5071 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 0.22324 0.06150 3.630 0.000283 *Lag1 -0.03843 0.02622 -1.466 0.142683 Lag2 0.06085 0.02656 2.291 0.021971 * ---Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1(Dispersion parameter for binomial family taken to be 1) Null deviance: 1494.6 on 1087 degrees of freedomResidual deviance: 1486.5 on 1085 degrees of freedomAIC: 1492.5Number of Fisher Scoring iterations: 4c
预测第一个数据结果
predict.glm(glm.fit, Weekly[1, ], type = "response") > 0.51: TRUE
d
编写循环,实现LOOV
# 初始化向量count = rep(0, dim(Weekly)[1])for (i in 1:(dim(Weekly)[1])) { glm.fit = glm(Direction ~ Lag1 + Lag2, data = Weekly[-i, ], family = binomial) pred_direction = predict.glm(glm.fit, Weekly[i, ], type = "response") > 0.5 true_direction= Weekly[i, ]$Direction == "Up" if (pred_direction != true_direction) count[i] = 1}490
mean(count)0.449954086317723
LOOCV的测试误差率为0.45
8.
下面模拟数据进行交叉验证
a
首先生成模拟数据
set.seed(1)x <- rnorm(100)y <- x-2*x^2+rnorm(100)在数据集中,n=100,p=2, Y = X − 2 X 2 + ϵ Y=X-2X^2+\epsilon Y=X−2X2+ϵ
b
画出X和Y的散点图
plot(x,y)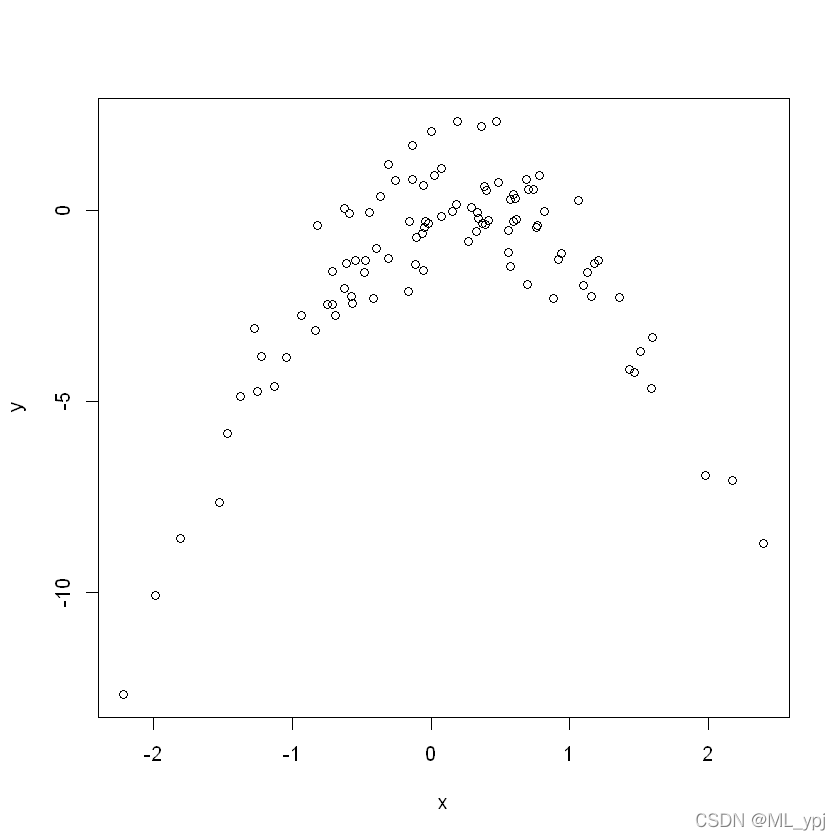
可以看出X和Y呈现二次型关系
c
计算四种拟合模型的LOOCV
# 线性回归library(boot)Data = data.frame(x, y)set.seed(1)glm.fit = glm(y ~ x)cv.glm(Data, glm.fit)$delta- 7.28816160667281
- 7.28474411546929
# 二次glm.fit = glm(y ~ poly(x, 2))cv.glm(Data, glm.fit)$delta- 0.937423637615552
- 0.937178917181123
# 三次glm.fit = glm(y ~ poly(x, 3))cv.glm(Data, glm.fit)$delta- 0.95662183010894
- 0.956253813731321
# 四次glm.fit = glm(y ~ poly(x, 4))cv.glm(Data, glm.fit)$delta- 0.953904892744804
- 0.953445283156601
可以看出在二次模型中,测试误差率降低很多,在更高次的模型中模型的测试误差没有明显下降,反而还升高了
d
set.seed(7)glm.fit = glm(y ~ x)cv.glm(Data, glm.fit)$delta- 7.28816160667281
- 7.28474411546929
# 二次glm.fit = glm(y ~ poly(x, 2))cv.glm(Data, glm.fit)$delta- 0.937423637615553
- 0.937178917181124
# 三次glm.fit = glm(y ~ poly(x, 3))cv.glm(Data, glm.fit)$delta- 0.95662183010894
- 0.956253813731322
# 四次glm.fit = glm(y ~ poly(x, 4))cv.glm(Data, glm.fit)$delta- 0.953904892744804
- 0.9534452831566
e
可以看出二次型的拟合效果最好,因为它最接近我们的真实关系
f
summary(glm.fit)
Call:glm(formula = y ~ poly(x, 2))Deviance Residuals: Min1Q Median3Q Max -1.9650 -0.6254 -0.1288 0.5803 2.2700 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.5500 0.0958 -16.18 < 2e-16 *poly(x, 2)1 6.1888 0.9580 6.46 4.18e-09 *poly(x, 2)2 -23.9483 0.9580 -25.00 < 2e-16 *---Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1(Dispersion parameter for gaussian family taken to be 0.9178258) Null deviance: 700.852 on 99 degrees of freedomResidual deviance: 89.029 on 97 degrees of freedomAIC: 280.17Number of Fisher Scoring iterations: 2二次多项式回归的结果回归系数显著,和交叉验证的结果基本一致
9.
下面使用Boston数据来进行下列问题
a
估计medv的均值
library(MASS)set.seed(1)attach(Boston)Warning message:"package 'MASS' was built under R version 4.0.5"Attaching package: 'MASS'
The following object is masked from 'package:ISLR2': Boston
medv.mean = mean(medv)medv.mean22.5328063241107
b
估计medv均值的标准差
s d (μ^ ) = s d ( μ ) /n sd(\hat \mu) = sd(\mu)/\sqrt{n} sd(μ^)=sd(μ)/n
medv.err = sd(medv)/sqrt(length(medv))medv.err0.408861147497535
c
现在使用bootstrap来估计标准差,与b中进行比较
boot.fn = function(data, index) { mean(data[index])}library(boot)bstrap = boot(medv, boot.fn, 1000)bstrap
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:boot(data = medv, statistic = boot.fn, R = 1000)
Bootstrap Statistics : original bias std. errort1* 22.53281 -0.02542806 0.4023801结果为0.40238,比b中的结果略小
d
通过t.test()计算置信区间,和bootstrap的方法进行比较
t.test(medv)
One Sample t-testdata: medvt = 55.111, df = 505, p-value < 2.2e-16alternative hypothesis: true mean is not equal to 095 percent confidence interval: 21.72953 23.33608sample estimates:mean of x 22.53281 c(bstrap$t0 - 2 * 0.4119, bstrap$t0 + 2 * 0.4119)- 21.7090063241107
- 23.3566063241107
可以看出置信区间基本一致
e
下面估计medv的中位数
首先使用基于数据集给出median()函数的估计值
medv.med = median(medv)medv.med21.2
f
下面我们想要估计medv中位数的标准差,没有直接的函数计算中位数的标准差。下面我们使用bootstrap的方法
# 先编写函数计算medv的中位数boot.fn = function(data, index) {median(data[index])}# 使用bootstrap估计标准差boot(medv, boot.fn, 1000)
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:boot(data = medv, statistic = boot.fn, R = 1000)
Bootstrap Statistics : original bias std. errort1* 21.2 -0.00655 0.3688301中位数的标准差为0.369
g
我们还可以计算分位数的标准差,首先计算分位数,10%分位数
medv.tenth = quantile(medv, c(0.1))medv.tenth10%: 12.75
h
通过bootstrap估计分位数标准差
boot.fn = function(data, index){ quantile(data[index], c(0.1)) } boot(medv, boot.fn, 1000)
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:boot(data = medv, statistic = boot.fn, R = 1000)
Bootstrap Statistics : original bias std. errort1* 12.75 0.0176 0.505965710%分位数的标准差为0.51


