机器学习笔记 - Moore-Penrose 伪逆
一、伪逆概述
并非所有矩阵都有逆矩阵。逆用于求解方程组,在某些情况下,方程组没有解,因此逆不存在。然而,找到一个最小化误差的近似值是有意义的。例如,使用伪逆找到一组数据点的最佳拟合线。
Moore-Penrose 伪逆是SVD的直接应用。
正如我们在之前篇章中看到的,矩阵A的逆矩阵可用于求解方程Ax=b:
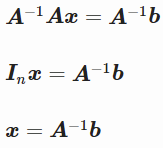
但是在方程组有0个或多个解的情况下,无法找到逆,也无法求解方程,这时候需要伪逆上场了。
伪逆记作![]() ,并
,并![]() ,并最小化
,并最小化![]()
以下公式可用于求伪逆:
![]()
(1)U、D 和 V 分别是 A 的左奇异向量、奇异值和右奇异向量。
(2)![]() 是A的伪逆,
是A的伪逆,![]() 是D的伪逆。
是D的伪逆。
(3)我们知道D是对角矩阵,因此D+可以通过取D的非零值的倒数来计算。
二、例1:伪逆计算
让我们看看如何计算它。 我们将创建一个非方阵 A,计算其奇异值分解及其伪逆。
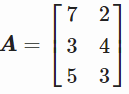
A = np.array([[7, 2], [3, 4], [5, 3]])U, D, V = np.linalg.svd(A)D_plus = np.zeros((A.shape[0], A.shape[1])).TD_plus[:D.shape[0], :D.shape[0]] = np.linalg.inv(np.diag(D))A_plus = V.T.dot(D_plus).dot(U.T)求得A_plus
array([[ 0.16666667, -0.10606061, 0.03030303],[-0.16666667, 0.28787879, 0.06060606]])我们现在可以使用 Numpy 的 pinv() 函数检查伪逆是否正确:
np.linalg.pinv(A)求得
array([[ 0.16666667, -0.10606061, 0.03030303],[-0.16666667, 0.28787879, 0.06060606]])数据一致,我们现在可以检查它是否真的是 A 的近似倒数。
我们已知![]() 并且
并且![]()
A_plus.dot(A)求得下面的矩阵,可以看出近似单位矩阵,对吧。
array([[ 1.00000000e+00, 2.63677968e-16],[ 5.55111512e-17, 1.00000000e+00]]) 就是说![]() ,也就是
,也就是![]()
计算伪逆的另一种方法是使用以下公式:
![]()
A_plus_1 = np.linalg.inv(A.T.dot(A)).dot(A.T)对于不同矩阵结果不如SVD方法精准。Numpy的函数pinv()就是使用SVD。
三、例2:使用伪逆求解超定线性方程组
对于这个例子,我们将考虑这组三个具有两个未知数的方程:
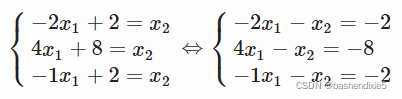
让我们可视化
x1 = np.linspace(-5, 5, 1000)x2_1 = -2*x1 + 2x2_2 = 4*x1 + 8x2_3 = -1*x1 + 2plt.plot(x1, x2_1)plt.plot(x1, x2_2)plt.plot(x1, x2_3)plt.xlim(-2., 1)plt.ylim(1, 5)plt.show()可视化效果如下,三条线没有交与一点,就是没有解。伪逆从最小二乘误差的角度求解系统:它找到最小化误差的解。

我们用矩阵形式表示
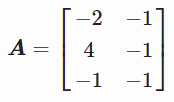
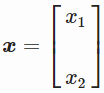
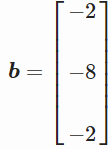
即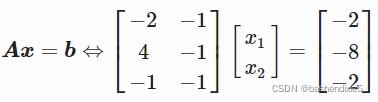
我们现在将计算 A 的伪逆:
A = np.array([[-2, -1], [4, -1], [-1, -1]])A_plus = np.linalg.pinv(A)A_plus求得
array([[-0.11290323, 0.17741935, -0.06451613],[-0.37096774, -0.27419355, -0.35483871]]) 取四位小数即,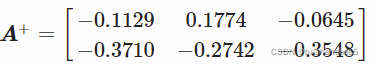
我们可以用它来找到 x:![]() 、
、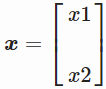
b = np.array([[-2], [-8], [-2]])res = A_plus.dot(b)res求得
array([[-1.06451613],[ 3.64516129]]) 即x坐标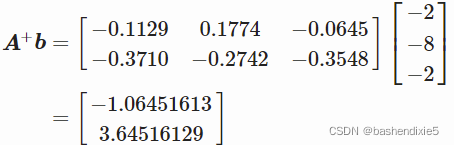
让我们绘制到图上看一下
plt.plot(x1, x2_1)plt.plot(x1, x2_2)plt.plot(x1, x2_3)plt.xlim(-2., 1)plt.ylim(1, 5)plt.scatter(res[0], res[1])plt.show()可视化效果如下
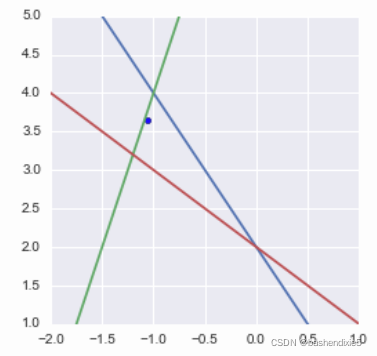
也许您会期望该点位于三角形的重心处。但情况并非如此,因为方程的缩放方式不同。
四、例3:直线拟合
此方法还可用于将线拟合到一组点。设有以下数据点:
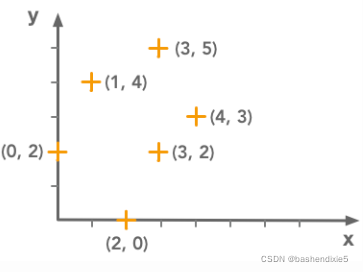
我们现有这组 x 和 y,我们要寻找最小化误差的线 y=mx+b。 可以将误差评估为拟合和实际数据点之间的差异之和。
我们可以用矩阵方程表示数据点:

请注意,这里的矩阵 A 表示系数的值。 1 列对应于截距(没有它,拟合将有跨越原点的约束)。 它给出了以下方程组:
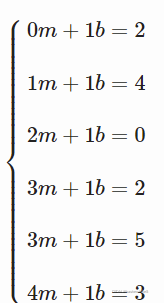
我们有一组方程 mx+b=y。 这些用于返回截距参数。 例如,在对应于第一个点的第一个方程中,我们有很好的 x=0 和 y=2。 这可能会令人迷惑,因为这里的向量 x 对应于系数。 这是因为我们正在寻找直线的系数而不是 x 和 y 未知数。
所以我们将构造这些矩阵并尝试使用伪逆来找到最小化误差(线与实际数据点之间的差异)的线的方程。
让我们创建 A 和 b 的矩阵并计算A的伪逆:
A = np.array([[0, 1], [1, 1], [2, 1], [3, 1], [3, 1], [4, 1]])b = np.array([[2], [4], [0], [2], [5], [3]])A_plus = np.linalg.pinv(A)求得伪逆如下
array([[ -2.00000000e-01, -1.07692308e-01, -1.53846154e-02, 7.69230769e-02, 7.69230769e-02, 1.69230769e-01],[ 6.00000000e-01, 4.00000000e-01, 2.00000000e-01, 4.16333634e-17, 4.16333634e-17, -2.00000000e-01]])带入公式x=A+b
coefs = A_plus.dot(b)求得拟合的参数。 斜率为 m=0.21538462,截距为 b=2.2。
array([[ 0.21538462],[ 2.2]])我们将绘制数据点和回归线:
x = np.linspace(-1, 5, 1000)y = coefs[0]*x + coefs[1]plt.plot(A[:, 0], b, '*')plt.plot(x, y)plt.xlim(-1., 6)plt.ylim(-0.5, 5.5)plt.show()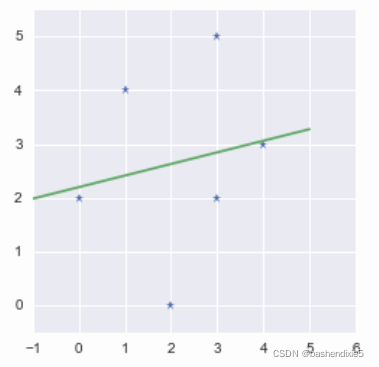
使用numpy库进行核验,使用polyfit函数对A和b进行拟合,得到如下结果,说明计算无误。
np.polyfit(A[:, 0], b, 1)array([[ 0.21538462],[ 2.2]])还有很多计算库或者在线拟合网页可以验证上面的计算,可以自行尝试。
五、例4:直线拟合
要查看具有更多数据点的过程,我们可以生成数据。
我们将生成一个包含 100 个具有随机 x 值和伪随机 y 值的点的列向量(参见下面的 reshape())。 Numpy.random 包中的函数 seed() 用于冻结随机化并能够重现结果:
np.random.seed(123)x = 5*np.random.rand(100)y = 2*x + 1 + np.random.randn(100)x = x.reshape(100, 1)y = y.reshape(100, 1)我们将通过添加一列 1 从 x 创建矩阵 A,就像我们在示例 3 中一样。
A = np.hstack((x, np.ones(np.shape(x))))A[:10]得到
array([[ 3.48234593, 1. ],[ 1.43069667, 1. ],[ 1.13425727, 1. ],[ 2.75657385, 1. ],[ 3.59734485, 1. ],[ 2.1155323 , 1. ],[ 4.90382099, 1. ],[ 3.42414869, 1. ],[ 2.40465951, 1. ],[ 1.96058759, 1. ]])我们现在可以找到 A 的伪逆并计算回归线的系数:
A_plus = np.linalg.pinv(A)coefs = A_plus.dot(y)coefs求得
array([[ 1.9461907 ],[ 1.16994745]])我们将点和直线可视化
x_line = np.linspace(0, 5, 1000)y_line = coefs[0]*x_line + coefs[1]plt.plot(x, y, '*')plt.plot(x_line, y_line)plt.show()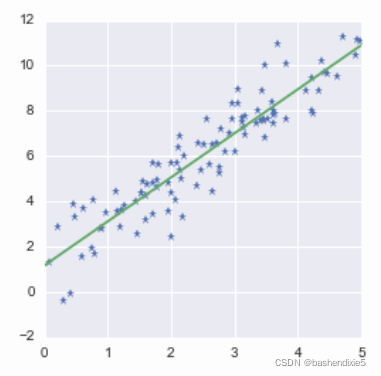
六、其它参考
您可以看到伪逆对这类问题非常有用!另外关于多项式拟合或拟合平面可以参考以下文章。
Opencv学习笔记 - 多项式求解和拟合_bashendixie5的博客-CSDN博客_opencv 多项式拟合曲线的函数类型有:双曲线型、对数型、指数型、多项式型等。对于最常见的曲线, 其特征接近于多项式型, 所以这里的曲线拟合问题就变成了多项式回归求解.一般情况下,对实际的点数据进行求解是无解的, 所以我们需要引入最小二乘法来求解。https://blog.csdn.net/bashendixie5/article/details/115176277Opencv学习笔记 - 使用最小二乘法拟合平面_bashendixie5的博客-CSDN博客_opencv 平面拟合https://blog.csdn.net/u012719076/article/details/113124887https://blog.csdn.net/liumangmao1314/article/details/54179526本文主要验证了博客上的最小二乘法拟合平面的。与 用matlab拟合出来的平面计算的点到直线的距离是一样的,而且系数也是一样的。说明了本方法的可行性。matlab中公式为z = c + ax +byoepncv中公式为Ax+By+Cz=D 将openc..
https://blog.csdn.net/bashendixie5/article/details/115413982


