【算法】——学会floodfill算法,周围都是舒适区
🌟 前言:Flood Fill——像素世界的「魔法棒」
想一键填满图中的封闭区域?
游戏角色为何不会穿墙?
这背后都藏着Flood Fill算法的魔法!
从画图软件的「油漆桶」到迷宫路径计算,
这个用DFS/BFS模拟「洪水蔓延」的算法,
能用10行代码解决许多看似复杂的问题。
本文将带你:
🔹 掌握递归经典实现
🔹 破解「4连通」与「8连通」的秘密
🔹 搞定一些经典问题
让我们开始这场「数字洪水」的冒险吧! 🎨🌊
\"好的算法就像魔法——Flood Fill就是那根点像素成金的魔杖\"
🌟 Flood Fill算法:数字世界的「颜料蔓延术」
🔍 算法本质
一种用于填充连通区域的经典算法,通过指定起点和填充规则,像倒颜料般自动填满封闭区域。
⚡ 核心思想
- 选定起点:从像素/网格的某个点出发
- 扩散规则:
- 4连通:上下左右4个方向
- 8连通:增加斜向共8个方向(更易漏边)
- 停止条件:遇到边界色或已填充区域
💡 两种经典实现
-
🔍 基础版(DFS递归实现)
#include #include using namespace std;// 4方向移动:上右下左const int dx[] = {-1, 0, 1, 0};const int dy[] = {0, 1, 0, -1};void dfs(vector<vector>& image, int x, int y, int oldColor, int newColor) { // 边界检查 + 颜色检查 if(x = image.size() || y = image[0].size() || image[x][y] != oldColor || image[x][y] == newColor) return; image[x][y] = newColor; // 填充新颜色 // 递归4个方向 for(int i = 0; i < 4; ++i) { dfs(image, x + dx[i], y + dy[i], oldColor, newColor); }}vector<vector> floodFill(vector<vector>& image, int sr, int sc, int newColor) { int oldColor = image[sr][sc]; if(oldColor != newColor) dfs(image, sr, sc, oldColor, newColor); return image;}⚡ 优化版(BFS队列实现)
#include #include // for pairvector<vector> floodFill_BFS(vector<vector>& image, int sr, int sc, int newColor) { int oldColor = image[sr][sc]; if(oldColor == newColor) return image; queue<pair> q; q.push({sr, sc}); image[sr][sc] = newColor; while(!q.empty()) { auto [x, y] = q.front(); q.pop(); for(int i = 0; i = 0 && nx = 0 && ny < image[0].size() && image[nx][ny] == oldColor) { image[nx][ny] = newColor; q.push({nx, ny}); } } } return image;}
🚀 实际应用场景
- 画图软件的油漆桶工具
- 游戏中的地图可达性判断
- 图像处理(背景替换/抠图)
- LeetCode「岛屿数量」「图像渲染」等题型
🌈 趣味比喻
把算法想象成病毒传播:
- DFS:一个感染者拼命传染能接触的所有人
- BFS:感染者们按批次有序传播
\"从一滴颜料到染满整个池塘——Flood Fill用代码诠释了什么是真正的『蔓延美学』\"
🌟 使用Flood Fill算法解决经典问题
经典例题:岛屿问题


思路:
直接遍历这个二维网格,遇到‘1’,就对这个网格相邻的最多四个网格以及它们相邻的区域进行判断
因为一个网格重复判断是没有意义的,并且相邻的为‘1’的网格视为一个网格
我们需要一个等大的bool类型的二维数组来一一对应二维网格中的某个网格是否已经被检查过
- 如果被检查过,则不用检查
- 如果没有被检查过,则需要对其以及其周边区域进行检查
这就是记忆化搜索,bool类型的二维数组就相当于一个记忆存储器
此外,因为需要对周边相邻的四个方向检查,我们可以提前创建两个数组来模拟四个方向
代码实现:
class Solution {public: int m; int n; int ret; vector<vector> vis; int numIslands(vector<vector>& grid) { m = grid.size(); n= grid[0].size(); vis=vector<vector>(m,vector(n,false)); for(int i=0;i<m;i++){ for(int j=0;j<n;j++){ if(grid[i][j] == \'1\'){ if(!vis[i][j]) { ret++; dfs(grid,i,j); } } } } return ret; } int dx[4]={0,0,1,-1}; int dy[4]={-1,1,0,0}; void dfs(vector<vector>& grid,int i,int j){ vis[i][j] = true; for(int k=0;k=0 && x=0 && y<n && !vis[x][y] && grid[x][y]==\'1\') dfs(grid,x,y); } }};经典例题:图像渲染
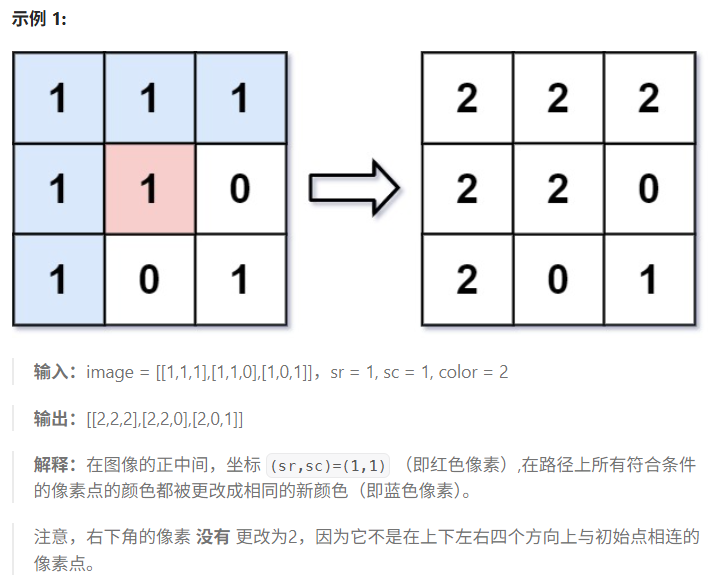
思路:
这种问题一般大差不差,有了上面一题的基础,这道思路也很清晰
直接对目标节点进行判断,如果需要上色就上色,并且对其周围区域以及周围区域的周围区域判断即可
代码实现:
class Solution {public: int m; int n; int prev; int dx[4]={1,-1,0,0}; int dy[4]={0,0,-1,1}; void dfs(vector<vector>& image,int i,int j,int color){ image[i][j]=color; for(int k=0;k=0 && x<m && y=0 && image[x][y] == prev){ dfs(image,x,y,color); } } } vector<vector> floodFill(vector<vector>& image, int sr, int sc, int color) { if(color == image[sr][sc]) return image; m = image.size(); n = image[0].size(); prev=image[sr][sc]; dfs(image,sr,sc,color); return image; }};经典例题:太平洋大西洋水流问题

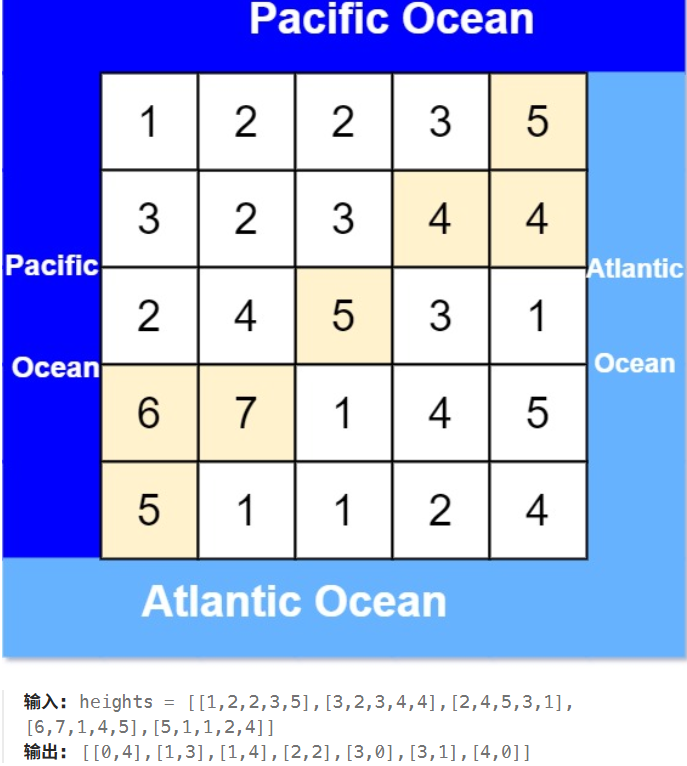
如果是以前,大家会连这道题目要干什么都看不到,不信看看下面这位暴躁老哥的发言
思路:
题目要求我们输出既可以流向大西洋又可以流向太平洋的所有格子
- 一个格子要流向太平洋,就需要有一条可以递减格子路径到太平洋
- 一个格子要流向大西洋,就需要一条可以递减格子路径到大西洋
如例子中的[2,2]格子
- 它的右方向按照 5->3-1递减,流向大西洋
- 它的左方向按照 5->4->2递减,流向太平洋
所以,我们需要对一个格子进行深搜,在其周围找到一条通往大西洋 一条通往太平洋的路径
这是解题思路,但你落实下去,就会发现难得可怕
这时候,正面突破就行不通,我们就需要从其他方面思考一下
- 与其求一个格子,同时到太平洋、大西洋
- 不如先判断一个格子上的水,是否能到太平洋,再判断是否能到大西洋
两个的结果都是对的,则符合题目要求,输出即可
解题思路就变成:
- 先找到所有水流能流向太平洋的格子
- 再找到所有水流能流向大吸引的格子
- 在遍历一次所有格子,如果一个格子满足上述两个条件,就是我们需要的格子!
代码实现:
class Solution {public: int m = 0; int n = 0; int dx[4]={-1,1,0,0}; int dy[4]={0,0,-1,1}; void dfs(int i,int j,vector<vector>& vis,vector<vector>& heights){ vis[i][j]=true; for(int k=0;k<4;k++){ int x = i+dx[k]; int y = j+dy[k]; if(x=0 && y=0 && !vis[x][y] && heights[i][j] <= heights[x][y] ) { dfs(x,y,vis,heights); } } } vector<vector> pacificAtlantic(vector<vector>& heights) { m=heights.size(); n=heights[0].size(); vector<vector> re_value; vector<vector> atl(m,vector(n,false)); vector<vector> pac(m,vector(n,false)); for(int j=0;j<n;j++){ dfs(0,j,pac,heights); dfs(m-1,j,atl,heights); } for(int i=0;i<m;i++){ dfs(i,0,pac,heights); dfs(i,n-1,atl,heights); } for(int i=0;i<m;i++){ for(int j=0;j<n;j++){ if(pac[i][j] && atl[i][j]){ re_value.push_back({i,j}); } } } return re_value; }};🌟 结语:Flood Fill的边界与想象
Flood Fill算法就像数字世界的水彩笔,用最简单的规则解决了区域填充的核心问题。从图像编辑软件的魔术棒到游戏地图的可达性判断,这个经典算法的应用远比我们看到的更广泛。
本文介绍的实现方式只是冰山一角。在实际开发中,针对不同场景可能需要考虑内存优化、并行计算等进阶技巧。但无论形式如何变化,其核心思想始终如一:通过系统性的蔓延规则,完成区域的智能填充。
当你下次使用绘图软件时,不妨想想背后这个精妙的算法。或许这就是编程的魅力——用简洁的代码逻辑,实现看似复杂的视觉魔法。
\"好的算法如同魔法,Flood Fill正是那支点石成金的魔杖。\"
继续探索吧,更多算法奇迹等着你去发现! 🚀



