FPGA实现AM数字调制_fpga实现am调制
一、序言
25年全国电赛临近,我这边考完期末就立马投入到了紧张刺激的备赛中,虽然今年是第三年参赛的老队员了,但一些基础知识还是需要复习一下,同时学习一些FPGA知识,去年有一道题就是因为我们不会FPGA做不了,今年争取把FPGA搞会。
目前正在做23年D题,因为刚会FPGA,手里没有积累的代码和资料,所以边问AI边手搓,AI生成的代码大家看看就好,千万别全信,我改他生成的代码改了好久,而且很多数据格式、位宽、运算都有错误,所以AI仅适用于搭建框架,具体的算法还是要自己来写。
我们先来回顾一下这道题:


基础部分就这些,先不好高骛远搞发挥部分,那么咱们一点一点开始,先做AM调制
二、AM调制
1.实现思路
本题要求载波频率2MHz,调幅系数(0.3~1.0)
数字调制的AM公式参考如下
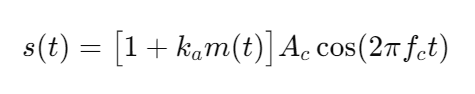
在FPGA内部做数字调制时,幅值Ac可暂时忽略,在FPGA内部,我们均采用归一化调制,即令调制信号m(t)和载波均为[-1,1)的归一化信号,此时调幅系数直接等于ka,简化了FPGA内部计算,这是大家可能会提出一点疑惑——在FPGA内部都是二进制数据,DDS的ROM表里存的都是形如-128~127(8位)、-8192~8191(14位)的二进制数据,怎么归一化为[-1,1)呢?
2.定点数
这就要用到二进制定点数了,二进制定点数格式的表示方法被记为SI(N)F(M),S表示为有符号数, N比特整数位, M比特小数位。 例如:SI9F7表示:有符号数,9比特整数位,7比特小数位。其实理解起来也蛮简单,就是把原来的数据线性缩小到了所规定的范围,例如:对于8bit数据,令其为SI1F7,表示有符号数,整数1位(含符号位),小数位7位,因此该计数法表示的浮点数范围为[-1,1-1/2^n),这里n=7(小数位),看到这里大家可以发现,二进制定点数是存在最小精度限制而带来的误差的,最小精度1/2^n,所以当小数位越多,误差越小。理解起来有点抽象,详细内容大家可以找找资料。
那么再阐明定点数的两种运算规律:
乘法:两个定点数相加,设其定点格式分别为 SI(N1)F(M1) 和 SI(N2)F(M2),设 N1 > N2, M1 > M2。
- 全精度乘法结果的字长是 SI(N1+N2)F(M1+M2)
- 乘法数据字长是以小数点为中心, 分别向两端扩展
- 通常保留 M1 位小数字长, 即可满足精度需求
- 小数截尾时,如果对精度有要求, 则需要考虑四舍五入问题
加法:两个定点数相加,设其定点格式分别为 SI(N1)F(M1) 和 SI(N2)F(M2), 设 N1 > N2, M1 > M2。
- 首先需要进行数据对齐, 即两个定点数的小数字长, 整数字长分别一致
- 即,在小数字长较小的数据低位补零, 在整数字长较小的数据高位符号扩展
- 字长调整后, 两个数据的字长均为 SI(N1)F(M1)
- 为避免溢出, 还需将整数字长扩充1位
- 加法结果的字长格式为 SI(N1+1)F(M1)
- 对于变量字长无法扩充的情况,则为了避免溢出, 将加数进行算术右移,抛弃小数部分,从而为整数部分留出更多空间。
了解了以上内容,就可以做算法了
3.AM实现
- 生成载波:可以参考我之前发的DDS设计,自行计算好频率字、写好正弦波ROM表,输出一个频率为2MHz,数据位宽14位的正弦波数据

- 生成调制信号:23年D题的说明中要求调制信号要1k、2k、3k、4k、5k可调,为了后续单片机控制框架的测试及实现,我这里先用按键进行遍历调整,也很简单,和载波大差不差,只不过这次要加一个频率字的输入接口,便于调整频率、、
- AM调制:在这一环节,要小心小心再小心,因为涉及到了有符号定点数的相乘,数据的位宽、符号位的取用都很容易出错,我在这里自查了很久才揪出错误
// ========== AM调制计算 ========== // Step1:Ma × mod_sig → Q2.26(28位) (* keep *)wire signed [2*RD_WL-1:0] mult_m_sig_ma;//加(* keep *)防止电路综合时将信号优化掉,便于算法的检查 assign mult_m_sig_ma = $signed(mod_sig) * $signed(Ma); // 14x14 = 28位、//Ma为调制系数(0.3~1),也是用key可调//上面两个数据相乘,范围不会超过[-1,1),继续保留一位整数 // Step2:右移13 → Q1.13 (* keep *)wire signed [RD_WL:0] scaled_mod_sig; // Q2.13,用于加常数1.0 assign scaled_mod_sig = mult_m_sig_ma >> 13; // Step3:加 1.0(Q2.13 中的1.0是 15\'sd8192) (* keep *)wire signed [RD_WL:0] mod_factor; assign mod_factor = scaled_mod_sig + 15\'sd8192;//注意:此时的数据范围已经超出[-1,1),整数位至少保留2位 // Step4:与carrier相乘 → Q3.26(15×14 = 29位) (* keep *)wire signed [2*RD_WL:0] mult_carrier_amp; assign mult_carrier_amp = (carrier_data) * (mod_factor); // Step5:右移14 → Q2.12(截位输出) (* keep *)wire signed [14:0] final_wave; assign final_wave = mult_carrier_amp >> 14;//Q2.12 // Step6:输出截断 always @(posedge I_CLK) begin if (I_RST) begin O_WAVE <= 0; end else begin O_WAVE <= final_wave[14:1]^ 14\'b1000_0000_0000_00;//输出给到DAC,因此高位取反转为无符号数 end 还要补充一点,我这里用的是Cyclone的芯片,所以用的是quartus,在检查算法和数据类型时,signaltap是一个很好用的工具。
核心部分就是这些,之后我们实验看看效果
三、实测
整个设计构建如下:
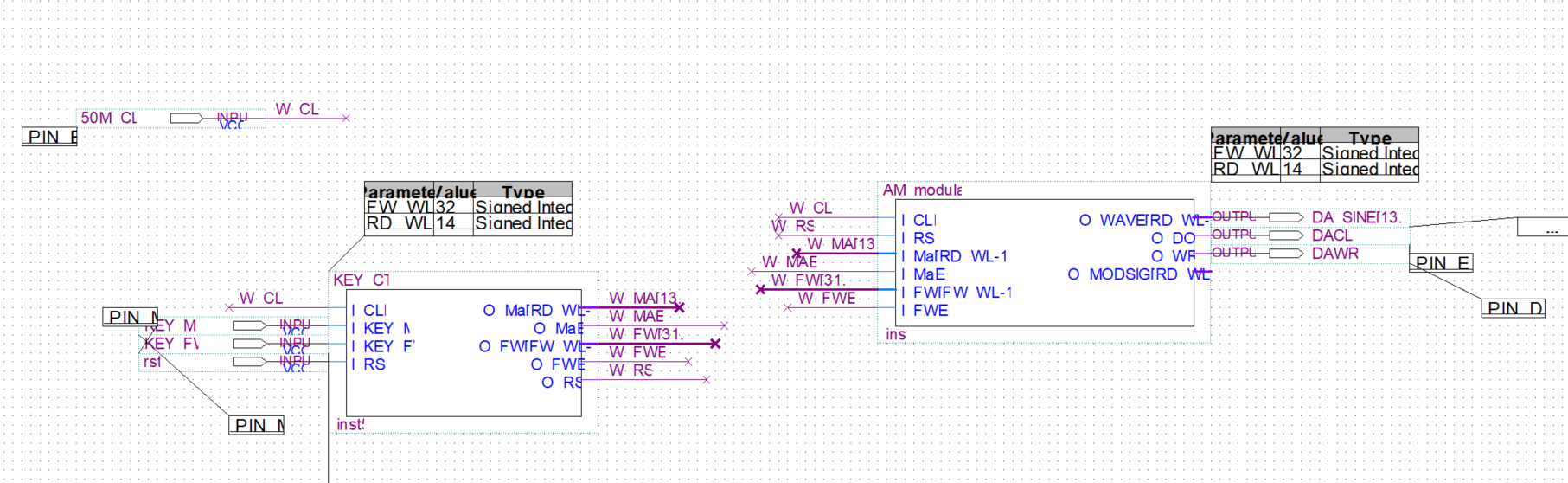
前级是按键控制模块,后级接AM调制模块,实现按键可控调制信号频率及调幅系数
主板+DA扩展:

输出的AM波形:
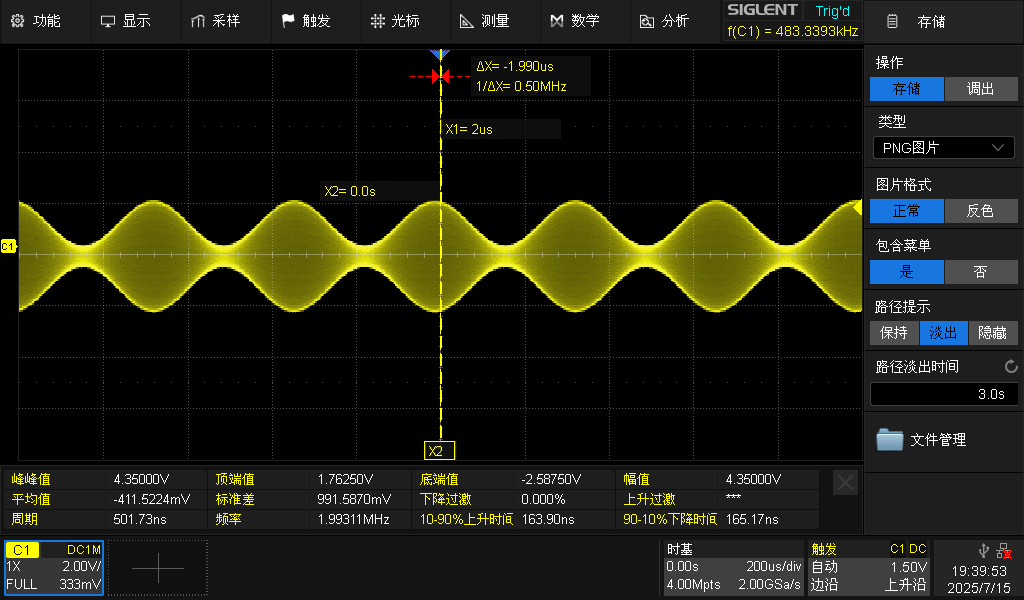
将示波器信号保存以mat.格式保存下来,导入到matlab中做频域分析,fs=1GHz,生成的频谱如下
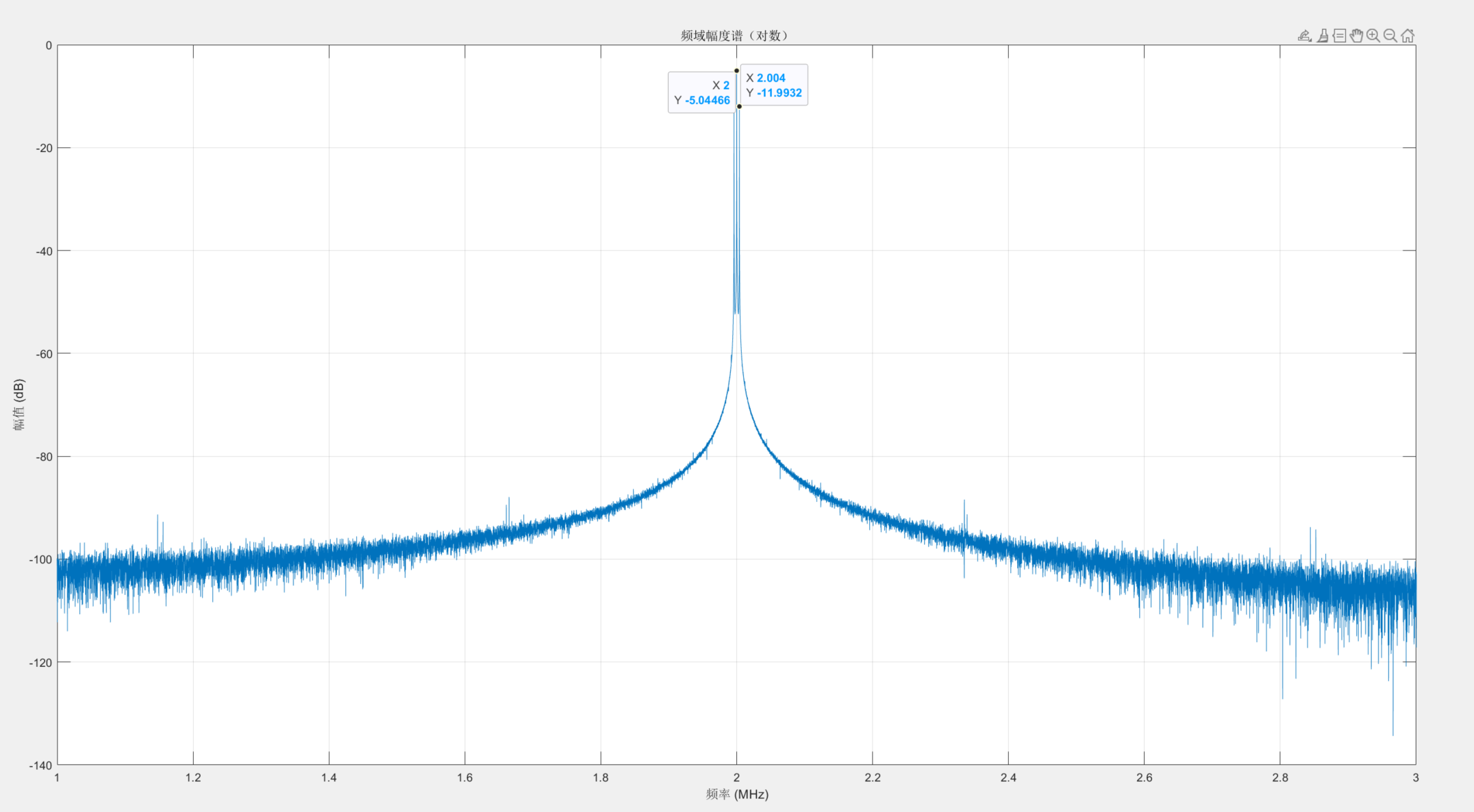
频谱结果表示,在2MHz处有一主峰,在其左右两侧距离4KHz处有两个小尖峰,结果符合预期的载波2MHz,调制信号4KHz。紧接着我们分析一下该信号的调幅系数,调幅系数的值与边带和载波幅度比有关,公式为:
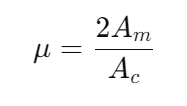
在matlab中做频谱分析,提取出最大的三个峰,并取最大峰值为Ac,取其余两个峰(边带)的平均值作为Am,最后计算。
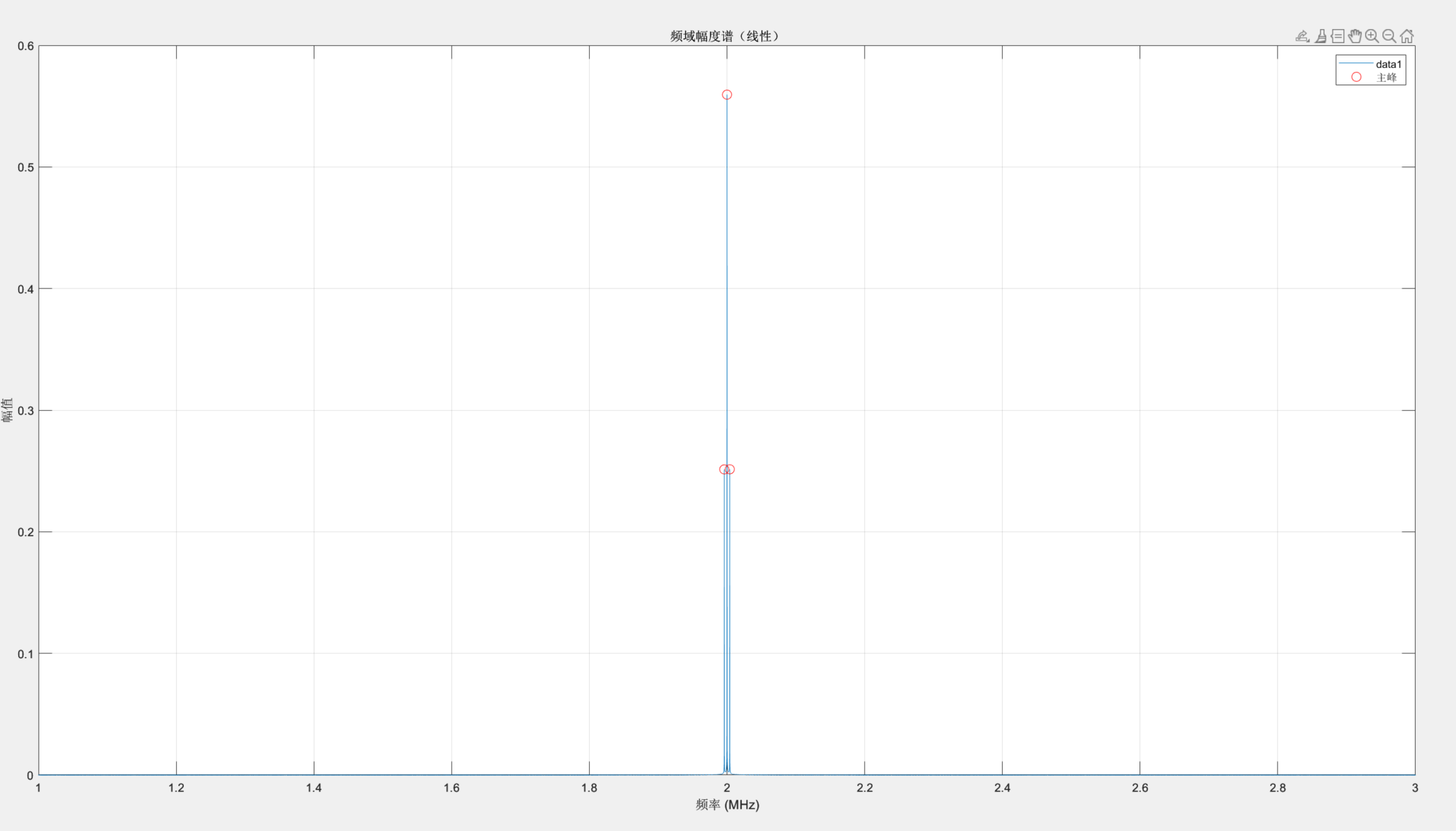
可以看出找到了这三个峰,并得出了结果
![]()
输出端调制系数0.9,接收端计算出的调制系数0.899,相对误差0.111%,比较精确。接下来做解调:
% 1. 全波整流(包络提取的第一步)envelope = double(abs(sig));% 2. 设计低通滤波器(截止频率略高于调制信号频率,例如 200 kHz)fc_lp = 200e3;% 截止频率 200 kHzorder = 2; % 5阶巴特沃斯滤波器[b, a] = butter(order, fc_lp/(fs/2)); % 归一化截止频率% 3. 应用滤波器(使用 filtfilt 零相位滤波器)demod_sig = filtfilt(b, a, envelope);通过全波整流+低通滤波,得出解调信号,时域频域如下:
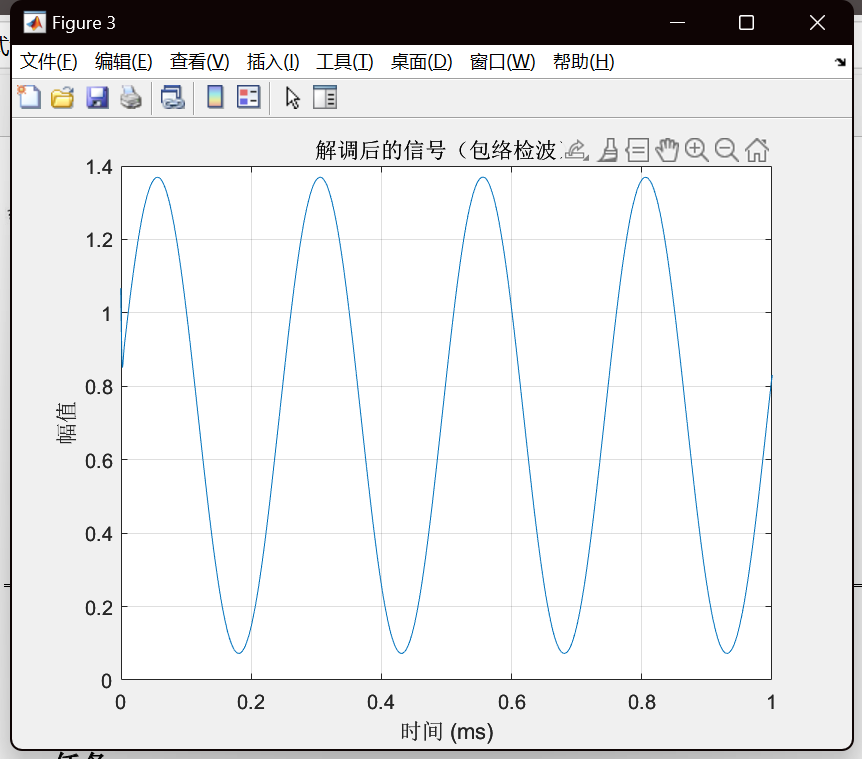
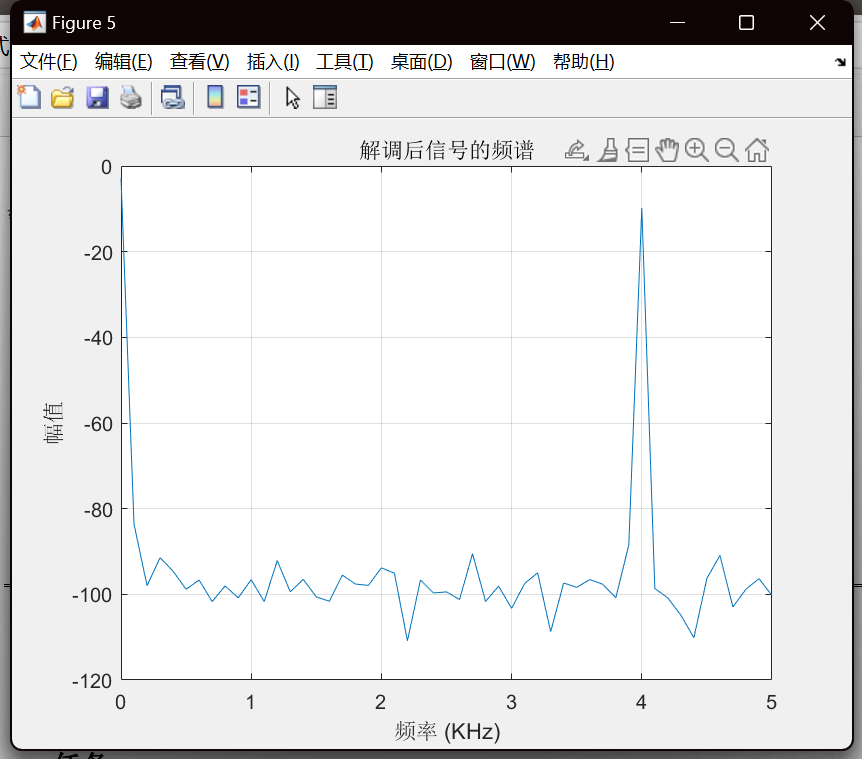
题目要求要对接收到的调制信号做调制方式识别,肯定要在单片机上用FFT做频域分析了,至于识别方式,我还在考虑,欢迎大家提出自己的见解。
四、总结
与我而言,如果真在电赛中遇到这道题,首先想到的AM调制方式一定是模拟电路调制,因为技术难度小、实现容易。但在实际的电路调试中,会存在各种实际的问题,同时由于器件精度、噪声,会导致很大的误差。相较于前者,使用FPGA进行数字调制的优势显而易见:电路中的各种人为因素导致的误差均可避免,信号准确、稳定,但与之相对应的,技术难度较大,需要付出一定学习成本。


