【java-数据结构】Java优先级队列揭秘：堆的力量让数据处理飞起来_java 定长优先队列

我的个人主页 我的专栏： 人工智能领域、java-数据结构、Javase、C语言，希望能帮助到大家！！！ 点赞👍收藏❤

---

引言

在开发中，尤其是需要处理大量数据或者进行任务调度的场景下，如何高效地管理数据的顺序和优先级是一个至关重要的问题。Java 提供了优先级队列（PriorityQueue），它基于堆（Heap）实现，能够以高效的方式管理数据的优先级。在本文中，我们将深入探讨优先级队列的工作原理，特别是堆的作用，并通过示例代码帮助你更好地理解其应用。

一、什么是优先级队列？

优先级队列（Priority Queue）是一种队列数据结构，其中每个元素都包含一个优先级，队列总是按元素的优先级顺序进行排序。与普通队列（先进先出 FIFO）不同，优先级队列确保每次从队列中移除的元素是具有最高优先级的元素。有些场景下，使⽤队列显然不合适，⽐如：在⼿机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话；初中那会班主任排座位时可能会让成绩好的同学先挑座位。

在 Java 中，PriorityQueue 是基于堆的实现。堆是一种特殊的二叉树结构，满足特定的顺序性质：最大堆保证每个父节点的值大于等于其子节点的值，而最小堆则相反。

二、堆的基本原理

JDK1.8中的PriorityQueue底层使⽤了堆这种数据结构，⽽堆实际就是在完全⼆叉树的基础上进⾏了⼀些调整。具有以下特点：

• 对于最大堆，父节点的值始终大于或等于子节点的值；
• 对于最小堆，父节点的值始终小于或等于子节点的值。

2.1 堆的概念

如果有⼀个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全⼆叉树的顺序存储⽅式存储在⼀个⼀维数组中，并满⾜：Ki <= K2i+1 且 Ki= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为⼩堆(或⼤堆)。
Java 中的 PriorityQueue 默认是最小堆，也就是说队列中最小的元素将具有最高的优先级。

堆的性质：
• 堆中某个节点的值总是不⼤于或不⼩于其⽗节点的值；
• 堆总是⼀棵完全⼆叉树。

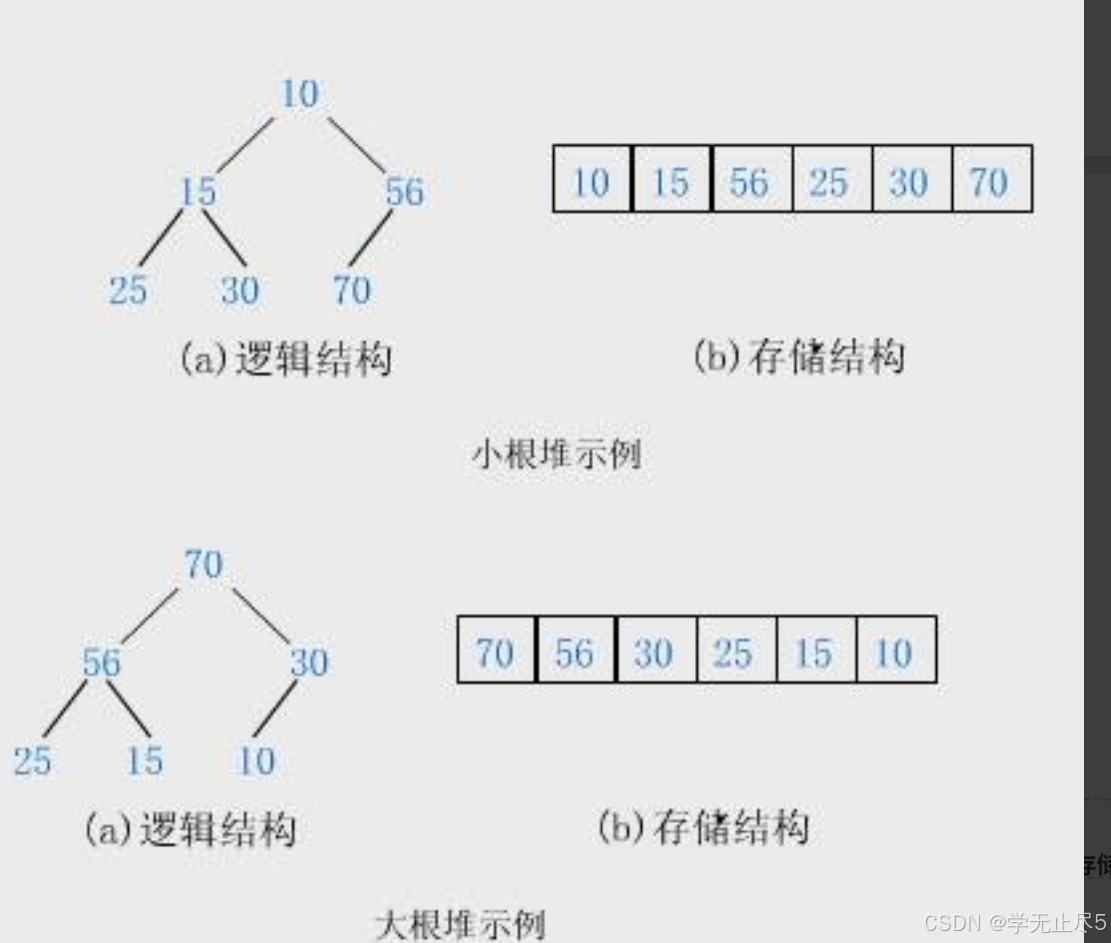
2.2 堆的存储⽅式

从堆的概念可知，堆是⼀棵完全⼆叉树，因此可以层序的规则采⽤顺序的⽅式来⾼效存储，

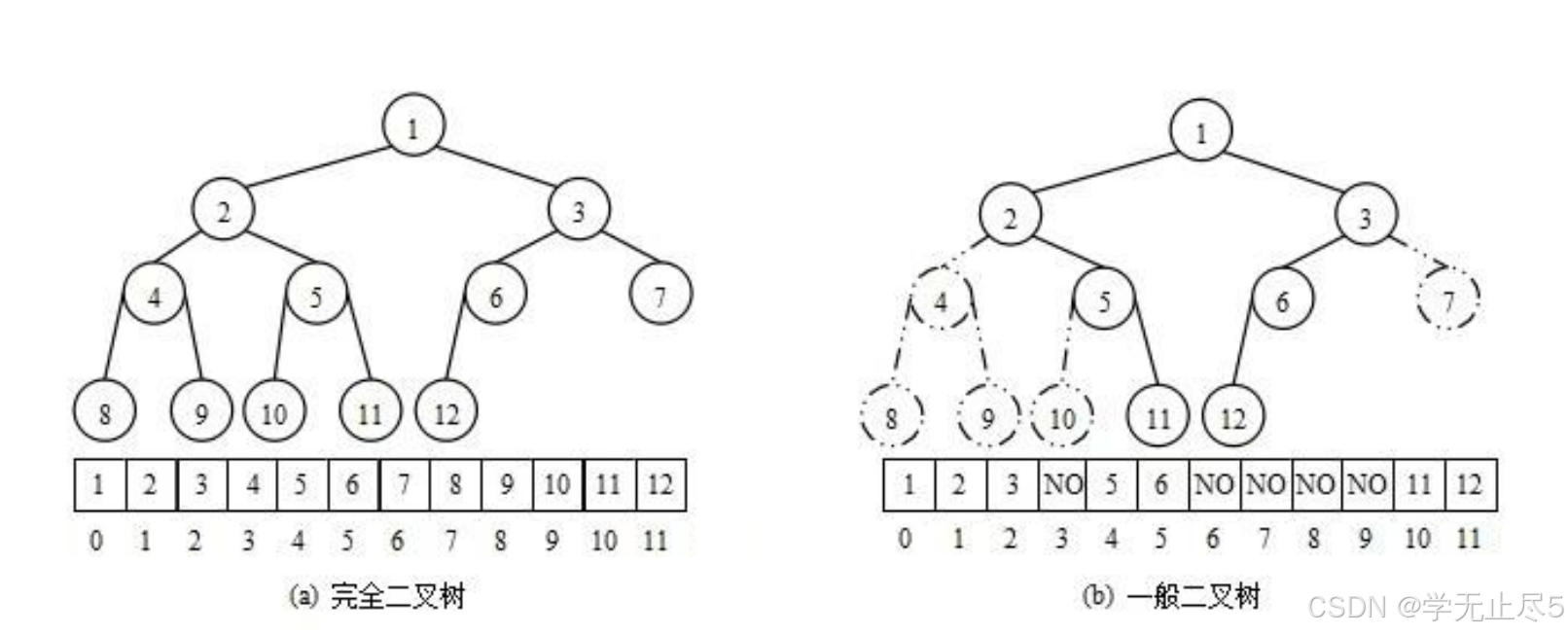
注意：对于⾮完全⼆叉树，则不适合使⽤顺序⽅式进⾏存储，因为为了能够还原⼆叉树，空间中必须 要存储空节点，就会导致空间利⽤率⽐较低。

将元素存储到数组中后，可以根据⼆叉树章节的性质5对树进⾏还原。假设i为节点在数组中的下标，则有：
• 如果i为0，则i表⽰的节点为根节点，否则i节点的双亲节点为 (i - 1)/2
• 如果2 * i + 1 ⼩于节点个数，则节点i的左孩⼦下标为2 * i + 1，否则没有左孩⼦
• 如果2 * i + 2 ⼩于节点个数，则节点i的右孩⼦下标为2 * i + 2，否则没有右孩⼦

三、堆操作时间复杂度

操作类型 描述 时间复杂度 插入元素 使用 add() 或 offer() 方法插入元素 O(log n) 删除最小元素 使用 poll() 方法移除并返回最小元素 O(log n) 查看最小元素 使用 peek() 方法返回堆顶元素而不移除 O(1) 获取堆大小 使用 size() 方法返回当前堆的元素数量 O(1)

3.1 建堆的时间复杂度

因为堆是完全⼆叉树，⽽满⼆叉树也是完全⼆叉树，此处为了简化使⽤满⼆叉树来证明(时间复杂度本
来看的就是近似值，多⼏个节点不影响最终结果)：

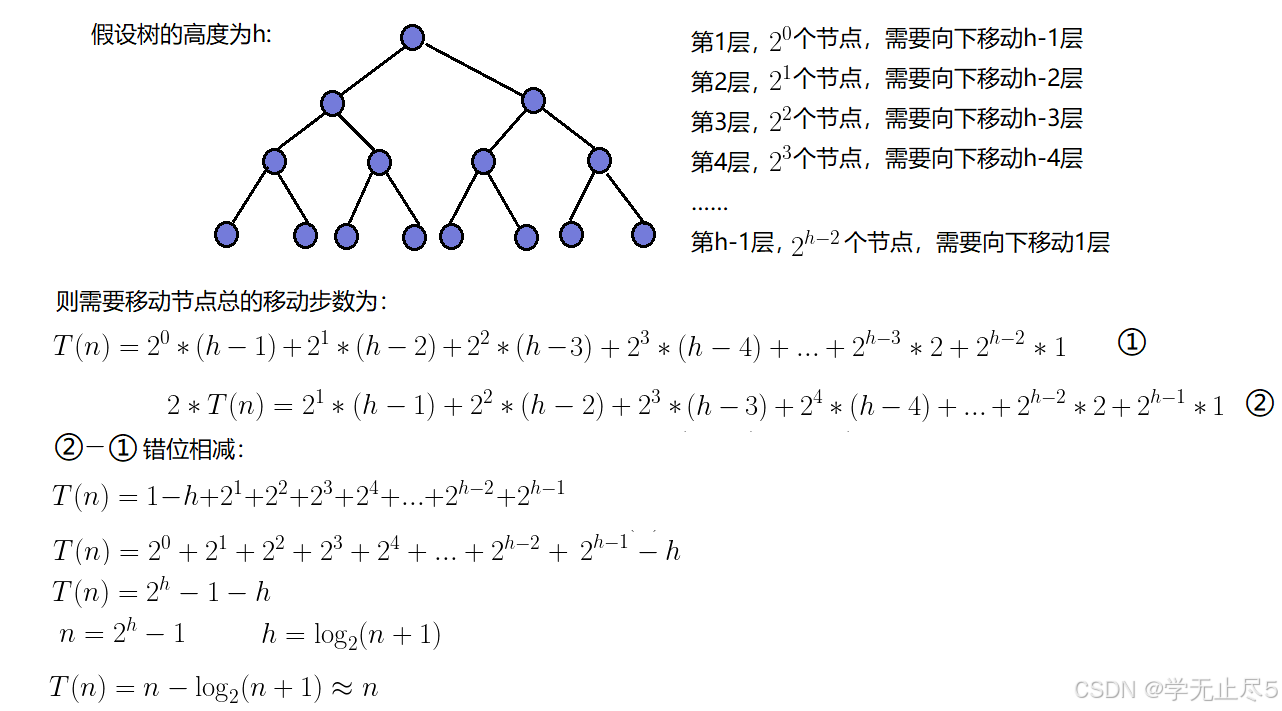
因此：建堆的时间复杂度为O(N)。

四、PriorityQueue 的基本操作

1. PriorityQueue中放置的元素必须要能够⽐较⼤⼩，不能插⼊⽆法⽐较⼤⼩的对象，否则会抛出 ClassCastException异常
2. 不能插⼊null对象，否则会抛出NullPointerException
3. 没有容量限制，可以插⼊任意多个元素，其内部可以⾃动扩容
4. 插⼊和删除元素的时间复杂度为
5. PriorityQueue底层使⽤了堆数据结构
6. PriorityQueue默认情况下是⼩堆—即每次获取到的元素都是最⼩的元素

4.1 插⼊/删除/获取优先级最⾼的元素

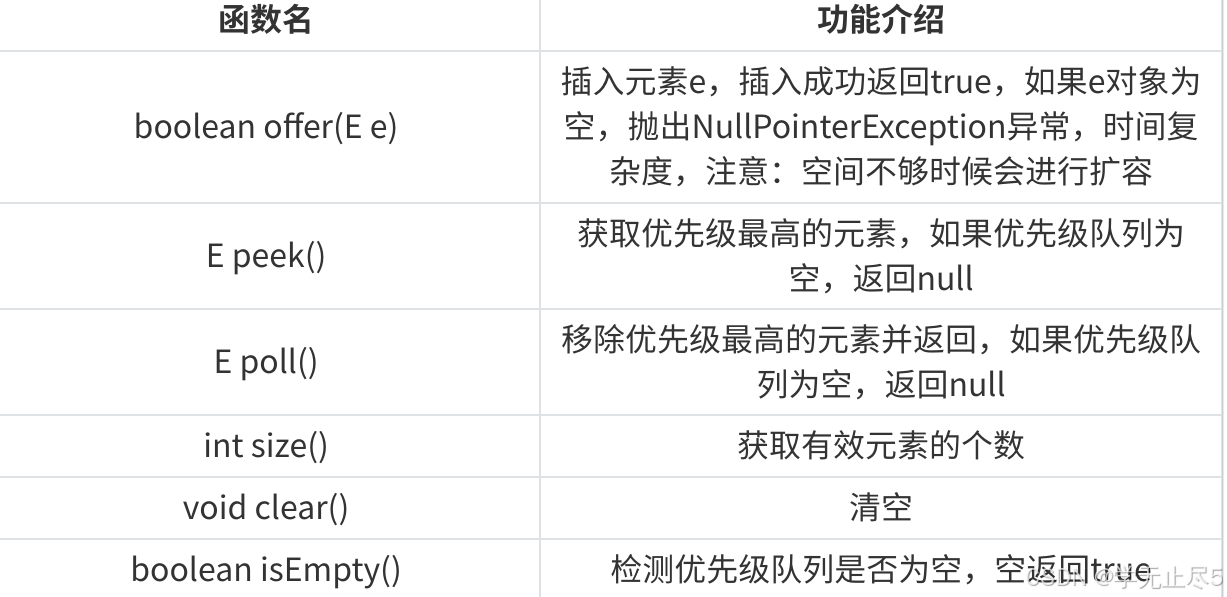
注意：优先级队列的扩容说明：

• 如果容量⼩于64时，是按照oldCapacity的2倍⽅式扩容的
• 如果容量⼤于等于64，是按照oldCapacity的1.5倍⽅式扩容的
•如果容量超过MAX_ARRAY_SIZE，按照MAX_ARRAY_SIZE来进⾏扩容

五、 构造一个最小堆的优先级队列

import java.util.PriorityQueue;public class PriorityQueueExample { public static void main(String[] args) { // 创建一个最小堆 PriorityQueue<Integer> pq = new PriorityQueue<>(); // 添加元素 pq.add(10); pq.add(5); pq.add(15); pq.add(7); // 打印并移除元素 while (!pq.isEmpty()) { System.out.println(pq.poll()); // 依次输出 5, 7, 10, 15 } }}

输出：

571015

在这个示例中，PriorityQueue 自动按照最小堆的规则对元素进行排序。每次调用 poll() 方法时，队列中优先级最高的元素（即最小的元素）会被移除。

六、 自定义优先级

假设我们有一个包含多个任务的列表，每个任务有一个优先级，我们希望按优先级顺序处理这些任务。我们可以通过实现 Comparator 接口来自定义优先级。

import java.util.PriorityQueue;import java.util.Comparator;class Task { String name; int priority; public Task(String name, int priority) { this.name = name; this.priority = priority; } @Override public String toString() { return name + \" (Priority: \" + priority + \")\"; }}public class CustomPriorityQueueExample { public static void main(String[] args) { // 自定义Comparator，按优先级降序排列 PriorityQueue<Task> pq = new PriorityQueue<>(new Comparator<Task>() { @Override public int compare(Task t1, Task t2) { return Integer.compare(t2.priority, t1.priority); // 优先级高的排前面 } }); // 添加任务 pq.add(new Task(\"Task 1\", 3)); pq.add(new Task(\"Task 2\", 5)); pq.add(new Task(\"Task 3\", 1)); pq.add(new Task(\"Task 4\", 4)); // 打印并移除任务 while (!pq.isEmpty()) { System.out.println(pq.poll()); } }}

输出：

Task 2 (Priority: 5)Task 4 (Priority: 4)Task 1 (Priority: 3)Task 3 (Priority: 1)

在这个例子中，PriorityQueue 被用来管理多个任务，并按照任务的优先级（从高到低）排序。

. 自定义优先级示例代码解释

步骤 代码示例 说明 创建优先级队列 PriorityQueue pq = new PriorityQueue(new Comparator() {...}); 创建一个带有自定义排序规则的优先级队列，按优先级降序排序 添加任务 pq.add(new Task(\"Task 1\", 3)); 向队列中添加一个新任务 打印任务 System.out.println(pq.poll()); 输出并移除队列中的优先级最高（优先级最大）的任务

---

七、常见堆的应用场景

应用场景 说明 示例 任务调度 根据任务的优先级执行任务，堆帮助管理和调度任务顺序 操作系统的调度程序，网络请求调度器 合并多个有序数据流 使用堆合并多个已排序的数据流，维持整体有序性 合并 k 个有序链表、流式数据处理 实时数据处理 动态地从数据流中获取最小/最大值 获取最近的数据流中的最大值/最小值，实时计算排名前N的元素 最短路径算法 在图算法（如 Dijkstra 算法）中，用堆优化路径的计算 Dijkstra 算法，最短路径计算中的优先级队列 K 个最大元素问题 找出数组中最大的 K 个元素 求数组中前 K 大的元素，堆排序方法

拓展：TOP-K问题：即求数据集合中前K个最⼤的元素或者最⼩的元素，⼀般情况下数据量都⽐较⼤。
⽐如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的⽅式就是排序，但是：如果数据量⾮常⼤，排序就不太可取了
(可能数据都不能⼀下⼦全部加载到内存中)。最佳的⽅式就是⽤堆来解决，基本思路如下：
1. ⽤数据集合中前K个元素来建堆

◦ 前k个最⼤的元素，则建⼩堆
◦ 前k个最⼩的元素，则建⼤堆

2. ⽤剩余的N-K个元素依次与堆顶元素来⽐较，不满⾜则替换堆顶元素
将剩余N-K个元素依次与堆顶元素⽐完之后，堆中剩余的K个元素就是所求的前K个最⼩或者最⼤的元素

八、总结

通过本文的介绍，我们了解了 Java 中优先级队列（PriorityQueue）的基本概念和实现原理。利用堆结构，优先级队列能够高效地管理数据并根据优先级进行处理。无论是任务调度、数据流合并，还是实时数据处理，堆都能发挥其强大的性能优势。

8.1 堆的优点

优点 说明 高效的优先级管理 通过堆结构，可以快速处理数据的优先级。插入和删除操作的时间复杂度为 O(log n)，适合动态数据处理。 无序输入，高效排序 堆无需输入数据有序，只需通过堆的结构来维护顺序。适用于合并已排序数据流。 内存占用少 堆是完全二叉树结构，相比于其他数据结构（如 AVL 树、红黑树）占用的内存较少。

8.2 优先级队列的优势与局限性

优势/局限性 说明 优势 - 对于频繁插入和删除操作非常高效。
- 适合任务调度、流式数据处理、最短路径问题等场景。 局限性 - 不支持按优先级范围查询或批量删除。
- 不是完全通用的排序工具，通常只适用于频繁访问最大或最小元素的场景。

8.3 堆与其他数据结构对比

数据结构 操作 时间复杂度 优势 局限性 堆 插入、删除、查看顶元素 O(log n) 高效管理优先级，适合动态数据处理。 不支持按特定条件的排序，无法直接获取中间元素。 数组 排序、查找 O(n log n) 方便查找和排序，简单易用。 插入、删除操作较慢，尤其是在无序数据中。 链表 插入、删除 O(1) 插入和删除效率高，尤其适合频繁变动的场景。 查找元素需要 O(n) 的时间，无法高效管理优先级。 红黑树 插入、删除、查找 O(log n) 支持高效的查找、插入和删除操作。 相较于堆，内存占用更大，且需要更多的平衡操作。 哈希表 查找、插入、删除 O(1) 查找操作极快，适合无序数据的快速检索。 不支持排序，不适合优先级管理。

前景：随着大数据和实时计算的不断发展，堆结构和优先级队列将在更多的算法优化和数据流处理中扮演重要角色，尤其是在机器学习、数据挖掘、搜索引擎优化等地方。

---